Konduksi panas
|
Read other articles:

BadianganMunisipalitasPeta Iloilo dengan Badiangan berwarna cerahNegaraFilipinaRegionWestern Visayas (Region VI)ProvinsiIloiloDistrikDistrik ke-3 di IloiloBarangay31Pemerintahan[1] • Wali kotaSuzette A. MamonLuas[2] • Total77,50 km2 (2,990 sq mi)Populasi (2010)[3] • Total26.218 • Kepadatan3,4/km2 (8,8/sq mi)Zona waktuUTC+8 (PST)Kode pos5033Kode area telepon33Situs webwww.badiangan.gov.ph Badiangan ad…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Aslan DoguzovInformasi pribadiNama lengkap Aslan Semyonovich DoguzovTanggal lahir 13 Januari 1991 (umur 33)Tinggi 1,77 m (5 ft 9+1⁄2 in)Posisi bermain GelandangInformasi klubKlub saat ini FC Alania-d VladikavkazKarier senior*Tah…

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut). …

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jindřichohradecké místní dráhy – news · newspapers · books · scholar · JSTOR (February 2014) (Learn how and when to remove this template message) vteJindřichohradecké místní dráhy Legend km km Jindřichův Hradec 0.000 Standard gauge lineto Veselí …

1964 United States Senate election in Washington ← 1958 November 3, 1964 1970 → Nominee Henry M. Jackson Lloyd J. Andrews Party Democratic Republican Popular vote 875,950 337,138 Percentage 72.21% 27.79% County resultsJackson: 50–60% 60–70% 70–80% 80–90% U.S. senator before election Henry M. Jackson Democratic Elected U.S. Senator Henry…

Kota KotamobaguKotaKotamobagu dilihat dari Puncak Passi LambangMotto: Kinalang - Paloko(Mongondow) Musyawarah - SepakatPetaKota KotamobaguPetaTampilkan peta SulawesiKota KotamobaguKota Kotamobagu (Indonesia)Tampilkan peta IndonesiaKoordinat: 0°44′N 124°19′E / 0.73°N 124.32°E / 0.73; 124.32Negara IndonesiaProvinsiSulawesi UtaraTanggal berdiri23 Mei 2007Dasar hukumUU Nomor 4 Tahun 2007[1]Jumlah satuan pemerintahan Daftar Kecamatan: 4Kelurahan: 33 P…

Keuskupan MetzDioecesis MetensisDiocèse de MetzKatedral MetzLokasiNegaraPrancisMetropolitSubyek langsung Tahta SuciStatistikLuas6.226 km2 (2.404 sq mi)Populasi- Total- Katolik(per 2013)1.045.066813,000 (77.8%)InformasiRitusLatinKatedralKatedral Santo Stefanus di MetzPelindungSanto StefanusKepemimpinan kiniPausFransiskusUskupJean-Christophe André Robert LagleizeEmeritusPierre René Ferdinand Raffin Uskup Emeritus (1987-2013)Situs webSitus Web Keuskupan Keuskup…

37th U.S. Attorney General Benjamin Brewster37th United States Attorney GeneralIn officeDecember 16, 1881 – March 4, 1885PresidentChester A. ArthurPreceded byWayne MacVeaghSucceeded byAugustus GarlandAttorney General of PennsylvaniaIn officeJanuary 16, 1867 – October 25, 1869GovernorJohn W. GearyPreceded byWilliam M. MeredithSucceeded byF. Carroll Brewster Personal detailsBornBenjamin Harris Brewster(1816-10-13)October 13, 1816Salem, New Jersey, U.S.DiedApril 4, 1888(1888-0…

Bay in Limestone Coast, South AustraliaGuichen BayThe Robe ObeliskGuichen BayLocation in South AustraliaLocationLimestone Coast, South AustraliaCoordinates37°7′14″S 139°45′58″E / 37.12056°S 139.76611°E / -37.12056; 139.76611[1]TypeBayBasin countriesAustraliaMax. length6 km (3.7 mi)[2]Max. width3.4 km (2.1 mi)[2]Max. depth11.3 m (37 ft)[2]SettlementsRobe Guichen Bay, (locally /ˈɡiːʃən/ GHEE…

Guelph RoyalsInformationLeagueIntercounty Baseball League (1919–present)LocationGuelph, OntarioBallparkDavid E. Hastings StadiumFounded1861Nickname(s)The RoyalsLeague championships9 1919 1920 1921 1932 1970 1993 1997 2003 2004 Former name(s) Guelph Royals Guelph CJOYs Guelph Royals (1962–63) Guelph Merchants (1958–61) Guelph Plymouths (1957) Guelph-Waterloo Royals (1954–56) Guelph Maple Leafs (1861–1953) Former league(s) Intercounty League (1911–18) Canadian League (1896–1911) Inte…

Design approach sensitive to environmental impacts See also: Sustainable design and Environmental design Ecodesign redirects here. For European directive, see European Ecodesign Directive. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ecological design – news · newspapers · books · scholar · JSTOR (August 202…

American lawyer Denise GeorgeGeorge in 2019.18th Attorney General of the United States Virgin IslandsIn officeMay 14, 2019 – January 1, 2023GovernorAlbert BryanPreceded byClaude WalkerSucceeded byCarol Thomas-Jacobs (acting) Personal detailsBornSaint Thomas, U.S. Virgin IslandsEducationUniversity of Maryland, College Park (BA)Howard University (JD) Denise N. George, also known as Denise George-Counts, is a U.S. Virgin Islands lawyer and former television news reporter who served as th…
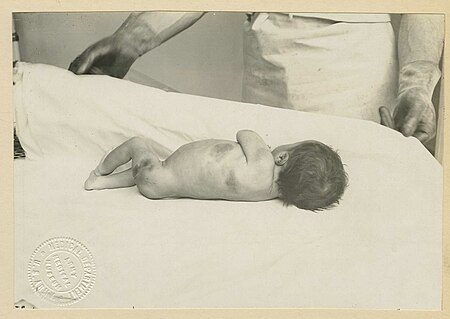
Purpura fulminans Données clés Symptômes Nécrose Traitement Spécialité Hématologie Classification et ressources externes CIM-10 D65 (ILDS D65.x20) CIM-9 286.6 DiseasesDB 34463 MeSH D011695 Mise en garde médicale modifier - modifier le code - voir Wikidata (aide) Le purpura fulminans est une forme grave, parfois mortelle, de sepsis sévère, touchant plus fréquemment les enfants et les adolescents. Il est défini comme l'association d'un sepsis sévère, d'une coagulation intravasculaire…

Medical condition This article is about the human condition. For peritonitis in cats, see Feline infectious peritonitis. Not to be confused with Peridontitis. Medical conditionPeritonitisOther namesSurgical abdomen, acute abdomen[1]Peritonitis from tuberculosisPronunciation/pɛrɪtəˈnaɪtɪs/ SpecialtyEmergency medicine, general surgerySymptomsSevere pain, swelling of the abdomen, fever[2][3]ComplicationsSepsis (sepsis is likely if not quickly treated), shock, acut…

Combat Vehicle 90 (CV90) adalah kendaraan lapis baja yang awalnya dikembangkan untuk Angkatan Darat Swedia oleh FMV, Hägglunds and Bofors, dan saat ini sudah diproduksi oleh BAE Systems. CV90 dan varian-variannya digunakan Angkatan Darat Denmark, Finlandia, Norwegia, Belanda, Swedia dan Swiss. CV90 diintegrasikan dengan meriam otomatis Bofors 40 mm atau Bushmaster 30 mm atau Bushmaster 35 mm/50 sebagai senjata utama. Stasiun senjata dikendalikan secara remot dan dipasangi senapan…

British novelist (1905–1983) Mary RenaultBornEileen Mary Challans[1](1905-09-04)4 September 1905Forest Gate, Essex, EnglandDied13 December 1983(1983-12-13) (aged 78)Cape Town, South AfricaOccupationWriterEducationSt Hugh's College, OxfordPeriod1939–1981GenreHistorical fiction, contemporary romance, war novel, gay literatureNotable works The King Must Die The Charioteer The Last of the Wine Fire from Heaven The Persian Boy Funeral Games PartnerJulie Mullard (1933–1983) Eileen M…

University of Bangka BelitungUniversitas Bangka BelitungTypePublicEstablished12 April 2006[1]RectorDr. Ibrahim, S.Fil., M.Si.LocationPangkalpinang, Bangka Belitung, Indonesia2°4′11.8″S 106°4′38.7″E / 2.069944°S 106.077417°E / -2.069944; 106.077417Websiteubb.ac.id University of Bangka Belitung (Indonesian: Universitas Bangka Belitung, abbreviated UBB) is a public university in Bangka Belitung province, Indonesia. Located just outside the provincial capi…

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Ни�…

City in South Carolina, United StatesChesnee, South CarolinaCityLocation of Chesnee, South CarolinaCoordinates: 35°8′54″N 81°51′43″W / 35.14833°N 81.86194°W / 35.14833; -81.86194CountryUnited StatesStateSouth CarolinaCountiesSpartanburg, CherokeeGovernment • MayorBruce MahaffeyArea[1] • Total1.07 sq mi (2.77 km2) • Land1.07 sq mi (2.77 km2) • Water0.00 sq mi (0.00&#…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Gangguan kelekatan adalah istilah umum yang digunakan untuk menggambarkan gangguan mood, tingkah laku, dan hubungan sosial yang timbul dari ketidaktersediaan perhatian dan pengasuhan cara sosialisasi yang normal dari sosok pemberi perhatian utama yang ter…






















































