Skyrmion
|
Read other articles:

Biografi ini tidak memiliki sumber tepercaya sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Al-Muktafi – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Biografi ini memerlukan lebih banyak catatan kaki unt…

Untuk kegunaan lain, lihat Get Married (disambiguasi). Get MarriedGenre Drama Komedi BerdasarkanGet Marriedoleh Hanung BramantyoSkenarioCassandra MassardiSutradaraAngling SagaranPemeran Prilly Latuconsina Jeff Smith Endy Arfian Debo Andryos Ajil Ditto Penata musikSlankNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode13ProduksiProduser eksekutif Sutanto Hartono Hermawan Sutanto Tina Arwin Produser Chand Parwez Servia Fiaz Servia Raza Servia SinematografiRico Manuel Na…

Raja Edward VIII dari Britania RayaKepala Persemakmuran Adipati WindsorPotret resmi, 1930anRaja Britania Raya dan Irlandia Utara Serta wilayah Alam Persemakmuran & Kaisar IndiaBerkuasa20 Januari 1936 – 11 Desember 1936(326 hari)PendahuluGeorge VPenerusGeorge VIPerdana Menteri Lihat daftar Joseph Aloysius LyonsWilliam Lyon Mackenzie KingÉamon de ValeraMichael Joseph SavageJames CraigJ. B. M. HertzogGodfrey HugginsStanley Baldwin Informasi pribadiKelahiranPangeran Edward dari York…

Golf tournament2017 PGA ChampionshipTournament informationDatesAugust 10–13, 2017LocationCharlotte, North Carolina, U.S.35°06′58″N 80°50′31″W / 35.116°N 80.842°W / 35.116; -80.842Course(s)Quail Hollow ClubOrganized byPGA of AmericaTour(s) PGA Tour European Tour Japan Golf Tour StatisticsPar71Length7,600 yards (6,949 m)[1]Field156 players, 75 after cutCut147 (+5)Prize fund$10,500,000€8,875,888Winner's share$1,890,000€1,597,660Champion Justin …
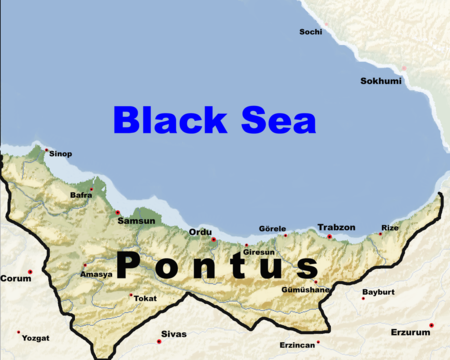
Halaman ini berisi artikel tentang lokasi geografis. Untuk dewa dalam mitologi Yunani, lihat Pontus (mitologi). Wilayah Pontus Pontus atau Pontos (Greek: Πόντος, translit: Póntoscode: el is deprecated , Latin: Pontuscode: la is deprecated ) adalah wilayah di pantai selatan Laut Hitam yang terletak di Turki modern. Kini, Pontus terletak di Turki modern. Wilayah ini terkenal akan kesuburannya. Ceri dibawa dari Pontus ke Eropa pada tahun 72 SM.[1] Referensi ^ Herbermann, C…

PT Pupuk Kalimantan TimurKantor pusat di BontangNama dagangPupuk KaltimJenisPerseroan terbatasIndustriBahan kimiaDidirikan7 Desember 1977; 46 tahun lalu (1977-12-07)KantorpusatBontang, IndonesiaWilayah operasiIndonesiaTokohkunciBudi Wahju Soesilo[1](Direktur Utama)Eka Sastra[2](Plt. Komisaris Utama)ProdukPupukAmoniakKawasan industriMinyak sawitMerekDaun BuahNPK PelangiPelangi AgroEcofertBiotaraBio SalinBio LKBiodexPendapatanRp 25,327 triliun (2021)[3]Laba bersihRp 6,…

Lambang kebesaran La Brosse-Montceaux. La Brosse-MontceauxNegaraPrancisArondisemenProvinsKantonMontereau-Fault-YonneAntarkomuneCommunauté de communes des Deux FleuvesPemerintahan • Wali kota (2008-2014) Bernard Metay • Populasi1599Kode INSEE/pos77054 / 2 Population sans doubles comptes: penghitungan tunggal penduduk di komune lain (e.g. mahasiswa dan personil militer). La Brosse-Montceaux merupakan sebuah komune di departemen Seine-et-Marne di region Île-de-France …

Scottish judge (1944-2011) The Right HonourableThe Lord Rodger of EarlsferryPC FBA FRSEJustice of the Supreme Court of the United KingdomIn office1 October 2009 – 26 June 2011Nominated byJack StrawAppointed byElizabeth IIPreceded byPosition establishedSucceeded byLord ReedLord of Appeal in OrdinaryIn office1 October 2001 – 30 September 2009Preceded byThe Lord ClydeSucceeded byPosition abolishedLord Justice General and Lord President of the Court of SessionIn office1…

Australian politician SenatorDeborah O'NeillO'Neill in 2023Senator for New South WalesIncumbentAssumed office 13 November 2013Preceded byBob CarrMember of the Australian Parliamentfor RobertsonIn office21 August 2010 – 7 September 2013Preceded byBelinda NealSucceeded byLucy WicksVice President of the New South Wales Labor PartyIncumbentAssumed office 9 December 2011Serving with Mark BoydPresidentMark LennonLeaderKristina KeneallyJohn RobertsonLuke FoleyPreceded byTara …

Neoaves Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:ПтицыПодкласс:Вее…

فيجيلانتي 8Vigilante 8 المطور لوكسوفلوكس الناشر أكتيفجن الموسيقى هوارد دروسين النظام نينتندو 64بلاي ستيشنإكس بوكس 360 تاریخ الإصدار 31 مايو 1998 نوع اللعبة مركبات قتالية النمط لاعب واحد، لاعبين التقييم ESRB: فيجيلانتي 8: سيكينت أوفينس تعديل مصدري - تعديل فيجيلان�…

Trompe-l'œil with a painted canvas and print of a landscape capriccio Jacobus Plasschaert or Jacob Plasschaert, spelling variation of name Plasgaert (c. 1689 – 21 November 1765 in Bruges) was a Flemish painter and teacher.[1] He is known for his trompe-l'œil still lifes and vanitas still lifes.[2] He was active in Bruges.[3] Life Jacobus Plasschaert was born around 1689 in an unknown location. When he registered with the guild of painters of Bruges on 6 April 1739, he…

Leipzig Leipsic[1],[2] De gauche à droite et de haut en bas : le centre-ville vu depuis Fockeberg, le monument de la Bataille des Nations de nuit, le tribunal administratif fédéral, l'ancien hôtel de ville sur la place du marché, la gewandhaus sur l'augustusplatz avec la city-hochhaus en arrière-plan et le gondwanaland au jardin zoologique. Armoiries Drapeau Administration Pays Allemagne Land Saxe District(Regierungsbezirk) Leipzig Arrondissement(Landkreis) Leipzig (ville-arrondisseme…

President of Peru (1985–1990 and 2006–2011) For other people named Alan García, see Alan García (disambiguation). In this Spanish name, the first or paternal surname is García and the second or maternal family name is Pérez. Alan GarcíaGarcía in 201053rd and 57th President of PeruIn office28 July 2006 – 28 July 2011Prime MinisterJorge Del CastilloYehude SimonJavier VelásquezJosé Antonio ChangRosario FernándezVice President1st Vice PresidentLuis Giampietri2nd Vice …

Bendera Sark Sark (dari bahasa Inggris; bahasa Prancis: Sercq, dialek Sercquiais: Sèr) adalah sebuah pulau yang merupakan bagian dari Bailiwick Guernsey, Kepulauan Channel, yang merupakan dependensi (hak milik) Takhta Britania (tapi bukan bagian dari United Kingdom). Penduduknya berjumlah 610 jiwa (2002). Mobil tidak boleh dikendarai di pulau ini. Industri utamanya adalah pariwisata dan finansial. Geografi Peta Bailiwick Guernsey. Sark terletak di bagian tenggara. Sark terbagi menjadi dua wilay…

LGBT+ rights in Mexico Part of the LGBT rights seriesLegal status ofsame-sex unions Marriage Andorra Argentina Australia Austria Belgium Brazil Canada Chile Colombia Costa Rica Cuba Denmark Ecuador Estonia Finland France Germany Greece Iceland Ireland Luxembourg Malta Mexico Netherlands1 New Zealand2 Norway Portugal Slovenia South Africa Spain Sweden Switzerland Taiwan United Kingdom3 United States4 Uruguay Recognized Israel5 Civil unions andregistered partnerships Bolivia Croatia Cyprus Czech R…

Il fascino discreto della borghesiaUna scena del filmTitolo originaleLe charme discret de la bourgeoisie Lingua originalefrancese, spagnolo Paese di produzioneFrancia, Italia, Spagna Anno1972 Durata96 min Rapporto1,66:1 Generecommedia, grottesco, satirico RegiaLuis Buñuel SoggettoLuis Buñuel, Jean-Claude Carrière SceneggiaturaLuis Buñuel, Jean-Claude Carrière ProduttoreSerge Silberman Casa di produzioneGreenwich Film Productions Distribuzione in italiano20th Century Fox Foto…

Dutch footballer (born 1991) This article needs to be updated. Please help update this article to reflect recent events or newly available information. (May 2024) Jordy Clasie Clasie playing for AZ in 2023Personal informationFull name Jordy Clasie[1]Date of birth (1991-06-27) 27 June 1991 (age 32)Place of birth Haarlem, NetherlandsHeight 1.69 m (5 ft 7 in)Position(s) Defensive midfielderTeam informationCurrent team AZNumber 8Youth career2000–2010 FeyenoordSenior car…

Dosa asal menurut doktrin teologi Kristen adalah kondisi pertama kali manusia berbuat dosa saat di Taman Eden. Walau Perjanjian Lama dan Perjanjian Baru yang sering membicarakan penuhnya dosa dalam diri manusia tidak memiliki kata-kata dosa asal dan Dosa leluhur, doktrin yang menggunakan kata-kata ini disebutkan berdasarkan pada ajaran Rasul Paulus dalam Roma 5:12-21 dan 1 Korintus 15:22. Setelah melihat doktrin ini, yang tidak ditemukan di teologi Yahudi, termuat secara terselubung di…

Trilogia degli IlluminatiTitolo originaleThe Illuminatus! Trilogy AutoreRobert Shea e Robert Anton Wilson 1ª ed. originale1975 Generefantascienza, satira Sottogeneredistopia Lingua originaleinglese Modifica dati su Wikidata · Manuale La Trilogia degli Illuminati (The Illuminatus! Trilogy o anche Illuminatus!)[1][2][3] è una trilogia di romanzi scritti da Robert Shea e Robert Anton Wilson originalmente pubblicati a partire dal 1975,[4] riuniti nel 1984 in u…


