Formelsammlung Geometrie

${\displaystyle {\sqrt[{n}]{x}}}$

Dieser Artikel ist eine Formelsammlung zum Thema Geometrie. Es werden mathematische Symbole verwendet, die im Artikel Liste mathematischer Symbole erläutert werden.

Die Formelsammlung zur euklidischen Geometrie ist ein Teil der Formelsammlung, in der auch Formeln der anderen Fachbereiche zu finden sind.

In den allermeisten Fällen gilt:

1. Punkte werden mit lateinischen Großbuchstaben ${\displaystyle (A,B,C,\ldots )}$ beschriftet.
2. Linien wie Geraden, Strecken und Bögen werden mit lateinischen Kleinbuchstaben ${\displaystyle (a,b,c,\ldots )}$ beschriftet.
3. Winkel werden mit griechischen Kleinbuchstaben ${\displaystyle (\alpha ,\beta ,\gamma ,\ldots )}$ beschriftet.

Im Folgenden werden Winkel im Gradmaß angegeben.

Nebenwinkel Die Summe von Nebenwinkeln beträgt immer 180°. ${\displaystyle \alpha +\beta =180^{\circ }}$
Scheitelwinkel Scheitelwinkel sind immer gleich groß. ${\displaystyle \alpha =\beta }$
Stufenwinkel Stufenwinkel an geschnittenen Parallelen sind immer gleich groß.
Wechselwinkel Wechselwinkel an geschnittenen Parallelen sind immer gleich groß.
Außenwinkel Im Dreieck ist ein Außenwinkel gleich der Summe der beiden nichtanliegenden Innenwinkel.
Winkelsummen Die Summe der Innenwinkel in einem Dreieck ist immer 180° Die Summe der Innenwinkel in einem ${\displaystyle n}$-Eck ist immer ${\displaystyle (n-2)\cdot 180^{\circ }}$ Die Summe der Außenwinkel beträgt in einem konvexen ${\displaystyle n}$-Eck stets 360° (unabhängig von der Eckenzahl ${\displaystyle n}$)

Verhältnisteilung: Um eine Strecke ${\displaystyle AB}$ in einem bestimmten Verhältnis (in ${\displaystyle n}$ gleiche Teile) zu teilen, zeichnet man zunächst einen beliebigen Strahl von ${\displaystyle A}$ aus, der nicht parallel zu ${\displaystyle AB}$ ist. Auf diesem trage man ${\displaystyle n}$ mal eine beliebig lange Strecke ab. Den erhaltenen Endpunkt ${\displaystyle C}$ verbinde man mit ${\displaystyle B}$ und zeichne die Parallelen zu ${\displaystyle BC}$ durch die bei der Unterteilung von ${\displaystyle AC}$ entstandenen Punkte. Deren Schnittpunkte mit ${\displaystyle AB}$ teilen ${\displaystyle AB}$ in ${\displaystyle n}$ gleiche Teile.

Die Standardbezeichnung für Dreiecke:

Eckpunkte

${\displaystyle A,B}$ und ${\displaystyle C}$. Die Ecke ${\displaystyle C}$ ist beim gleichschenkligen Dreieck der Treffpunkt der gleichen Seiten und beim rechtwinkligen Dreieck der Scheitel des rechten Winkels.

Seiten

${\displaystyle a}$ ist die der Ecke ${\displaystyle A}$ gegenüberliegende Seite, entsprechendes gilt für ${\displaystyle b}$ und ${\displaystyle c}$. Beim gleichseitigen Dreieck werden alle Seiten mit ${\displaystyle a}$ bezeichnet.^[1]

Winkel

${\displaystyle \alpha }$ ist der (Innen-)Winkel in Ecke ${\displaystyle A}$, ${\displaystyle \beta }$ der Winkel in Ecke ${\displaystyle B}$ und ${\displaystyle \gamma }$ der Winkel in Ecke ${\displaystyle C}$.

Figur	Flächeninhalt A	Umfang U	Bemerkung, Weiteres
Dreieck
Allgemeines Dreieck	${\displaystyle {\frac {1}{2}}gh={\frac {1}{2}}bc\sin \alpha }$ ${\displaystyle ={\frac {abc}{4R}}=k\cdot r}$ ${\displaystyle ={\sqrt {k(k-a)(k-b)(k-c)}}}$	${\displaystyle a+b+c}$	Letztere Flächenformel wird als Satz des Heron bezeichnet. ${\displaystyle k}$ ist der halbe Umfang, ${\displaystyle R}$ der Umkreisradius und ${\displaystyle r}$ der Inkreisradius.
Gleichseitiges Dreieck	${\displaystyle {\frac {1}{4}}a^{2}{\sqrt {3}}}$	${\displaystyle 3\cdot a}$	Alle Seiten sind gleich lang. Alle Winkel sind gleich groß (60°). Höhenlinien = Symmetrieachsen = Winkelhalbierende = Seitenhalbierende= Mittennormale
Gleichschenkliges Dreieck	${\displaystyle {\frac {1}{2}}c{\sqrt {a^{2}-{\frac {1}{4}}c^{2}}}}$	${\displaystyle 2a+c}$	Zwei Seiten sind gleich lang (Schenkel ${\displaystyle a}$ und ${\displaystyle b}$); die dritte Seite heißt Basis ${\displaystyle c}$ Die beiden Basiswinkel (${\displaystyle \alpha }$ und ${\displaystyle \beta }$) sind gleich groß. Die Höhenlinie durch ${\displaystyle C}$ halbiert den Winkel ${\displaystyle \gamma }$ und die Basis ${\displaystyle c}$.
Rechtwinkliges Dreieck	${\displaystyle {\frac {1}{2}}ab}$	${\displaystyle a+b+c}$	${\displaystyle \gamma =\alpha +\beta =90^{\circ }}$. Hypotenuse = längste Seite = Seite gegenüber dem 90°-Winkel. Katheten = Seiten, die den rechten Winkel bilden. Es gilt die Satzgruppe des Pythagoras (s. u.)
Viereck
Quadrat	${\displaystyle a^{2}}$	${\displaystyle 4\cdot a}$	Diagonale ${\displaystyle d=a\cdot {\sqrt {2}}}$
Rechteck	${\displaystyle a\cdot b}$	${\displaystyle 2\cdot (a+b)}$	Diagonale ${\displaystyle d={\sqrt {a^{2}+b^{2}}}}$
Raute (Rhombus)	${\displaystyle {\frac {1}{2}}ef=a^{2}\cdot \sin \alpha }$	${\displaystyle 4\cdot a}$	${\displaystyle e,f}$ = Diagonalen, ${\displaystyle \alpha }$ = beliebiger Innenwinkel.
Parallelogramm	${\displaystyle a\cdot h_{a}}$	${\displaystyle 2\cdot (a+b)}$	${\displaystyle h_{a}}$ ist die Höhe zur Seite ${\displaystyle a}$.
Trapez	${\displaystyle m\cdot h={\frac {1}{2}}(a+c)\cdot h}$	${\displaystyle a+b+c+d}$	${\displaystyle a,c}$ = parallele Seiten, ${\displaystyle m={\tfrac {1}{2}}(a+c)}$ = Mittellinie
symmetrischer Drachen (Deltoid)	${\displaystyle {\frac {1}{2}}ef}$	${\displaystyle 2\cdot (a+b)}$	${\displaystyle e,f}$ = Diagonalen.
Sehnenviereck	${\displaystyle {\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$ ${\displaystyle ={\frac {e\cdot (ab+cd)}{4R}}={\frac {f\cdot (ad+bc)}{4R}}}$	${\displaystyle a+b+c+d}$	Viereck mit Umkreis, ${\displaystyle R}$ Umkreisradius ${\displaystyle ={\frac {1}{4A}}{\sqrt {(ab+cd)(ac+bd)(ad+bc)}}}$, ${\displaystyle s}$ halber Umfang; ${\displaystyle e,f}$ Diagonalen: ${\displaystyle e={\sqrt {\frac {(ac+bd)(ad+bc)}{ab+cd}}}}$, ${\displaystyle f={\sqrt {\frac {(ab+cd)(ac+bd)}{ad+bc}}}}$
Tangentenviereck	${\displaystyle r\cdot (a+c)=r\cdot (b+d)}$	${\displaystyle a+b+c+d}$	Viereck mit Inkreis mit Inkreisradius ${\displaystyle r}$. Es gilt ${\displaystyle a+c=b+d}$
Polygone
Regelmäßiges Polygon	${\displaystyle {\frac {n\cdot r_{\mathrm {u} }^{2}\cdot \sin {\frac {360^{\circ }}{n}}}{2}}}$ ${\displaystyle =n\cdot r_{\mathrm {i} }^{2}\cdot \tan {\frac {180^{\circ }}{n}}}$ ${\displaystyle ={\frac {n\cdot l_{\mathrm {k} }^{2}\cdot \cot {\frac {180^{\circ }}{n}}}{4}}}$	${\displaystyle 2\cdot n\cdot r_{\mathrm {u} }\cdot \sin {\frac {180^{\circ }}{n}}}$ ${\displaystyle =2\cdot n\cdot r_{\mathrm {i} }\cdot \tan {\frac {180^{\circ }}{n}}}$ ${\displaystyle =n\cdot l_{\mathrm {k} }}$	${\displaystyle n}$ – Anzahl der Ecken ${\displaystyle r_{u}}$ – Radius des Umkreises, d. h. Entfernung vom Mittelpunkt zu einer Ecke ${\displaystyle r_{i}}$ – Radius des Inkreises, d. h. Entfernung vom Mittelpunkt zu einer Seitenmitte ${\displaystyle l_{k}}$ – Kantenlänge einer Seite des Polygons
Kreis
Kreis	${\displaystyle \pi \cdot r^{2}={1 \over 4}\cdot \pi \cdot d^{2}}$	${\displaystyle 2\cdot \pi \cdot r=\pi \cdot d}$	Es bezeichnet ${\displaystyle \pi =3{,}14159\ldots }$ die Kreiszahl.
Kreisring	${\displaystyle \pi \cdot (R^{2}-r^{2})}$	${\displaystyle 2\cdot \pi \cdot (R+r)}$	${\displaystyle R}$ = Außenradius, ${\displaystyle r}$ = Innenradius
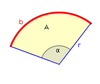
Kreisausschnitt	${\displaystyle \pi \cdot r^{2}\cdot {\alpha \over 360^{\circ }}={\frac {1}{2}}r^{2}\cdot \varphi }$ ${\displaystyle ={\frac {1}{2}}\cdot b\cdot r}$	${\displaystyle \pi \cdot r\cdot {\alpha \over 180^{\circ }}+2r=r(\varphi +2)}$	b = ${\displaystyle \pi \cdot r\cdot {\alpha \over 180^{\circ }}=r\cdot \varphi ;\quad \varphi =\alpha \cdot {\frac {\pi }{180^{\circ }}}}$ (Winkel im Bogenmaß)
Kreisabschnitt (Segment)	${\displaystyle {\frac {1}{2}}r^{2}\cdot (\varphi -\sin \varphi )}$	${\displaystyle r\cdot \left(2+{\sqrt {2-2\cos \varphi }}\right)}$	${\displaystyle \varphi =\alpha \cdot {\frac {\pi }{180^{\circ }}}}$ (Winkel im Bogenmaß)
Kegelschnitte
Ellipse	${\displaystyle \pi ab}$ ${\displaystyle ={\frac {1}{4}}\pi \cdot D\cdot d}$	${\displaystyle 4a\int \limits _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}(\sin t)^{2}}}\ \mathrm {d} t=4a\;E(\varepsilon )}$	Menge der Punkte, für die die Summe der beiden Abstände zu zwei gegebenen Punkten (Brennpunkten) konstant (${\displaystyle 2a}$) ist. Der Umfang lässt sich nicht mit elementaren Funktionen angeben (→ Elliptisches Integral). D,d großer und kleiner Durchmesser. Kartesische Koordinaten: ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
Hyperbel	Keine geschlossene Fläche	Keine geschlossene Kurve	Menge aller Punkte, für die die absolute Differenz der Abstände zu den Brennpunkten konstant 2a ist. Kartesische Koordinaten: ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
Parabel	Keine geschlossene Fläche	Keine geschlossene Kurve	Menge aller Punkte, deren Abstand zu einem speziellen festen Punkt (dem Brennpunkt) und einer speziellen Geraden (der Leitgeraden l) konstant ist. Kartesische Koordinaten: ${\displaystyle y^{2}=2px\,}$.

• Seitenhalbierende (Schwerlinien)
  • teilen einander im Verhältnis 2:1.
  • schneiden sich in einem Punkt, dem Schwerpunkt S des Dreiecks.
  • teilen die Dreiecksfläche in je zwei gleich große Teilflächen.

• Schnittpunkt der Mittelsenkrechten (Mittennormalen) = Mittelpunkt des Umkreises.

• Schnittpunkt der Winkelhalbierenden = Mittelpunkt des Inkreises.

• Höhenlinien
  • schneiden einander in einem Punkt H, dem Höhenschnittpunkt des Dreiecks.
  • Die Höhe h_c ist der Normalabstand des Punktes C zur Seite c (rechter Winkel bei D).

• Satz des Pythagoras

  Im rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Flächen der Quadrate über den Katheten.
  Sind ${\displaystyle a}$ und ${\displaystyle b}$ die Längen der Katheten und ${\displaystyle c}$ die Länge der Hypotenuse, dann gilt:

  ${\displaystyle a^{2}+b^{2}=c^{2}\,}$^[2]

• Kathetensatz

  Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächengleich dem Rechteck aus der Hypotenuse und der Projektion dieser Kathete auf die Hypotenuse.
  Mit den Bezeichnungen der untenstehenden Zeichnung gilt:

  ${\displaystyle a^{2}=p\cdot c,\ b^{2}=q\cdot c}$

• Höhensatz

  Im rechtwinkligen Dreieck ist das Quadrat über der Höhe auf der Hypotenuse flächengleich mit dem Rechteck aus den Hypotenusenabschnitten.
  Mit den Bezeichnungen der untenstehenden Zeichnung gilt:

  ${\displaystyle h^{2}=q\cdot p}$^[2]

  

Die Summe zweier Seiten eines Dreiecks ist stets größer als die dritte Seite.

Zwei Dreiecke sind kongruent bzw. deckungsgleich, wenn sie übereinstimmen in

1. drei Seiten (sss)
2. zwei Seiten und dem eingeschlossenen Winkel (sws)
3. zwei Seiten und dem Gegenwinkel der längeren Seite (Ssw)
4. einer Seite und den beiden anliegenden Winkeln (wsw)

Zwei Dreiecke sind ähnlich, wenn

1. drei Paare entsprechender Seiten das gleiche Verhältnis haben
2. zwei Paare entsprechender Seiten das gleiche Verhältnis haben und die von diesen Seiten eingeschlossenen Winkel übereinstimmen
3. zwei Paare entsprechender Seiten dasselbe Verhältnis haben und die Gegenwinkel der längeren Seiten übereinstimmen
4. zwei Winkel übereinstimmen

1. Strahlensatz: Wird ein Zweistrahl durch zwei parallele Geraden geschnitten, so stehen die Strahlenabschnitte des ersten Strahles im gleichen Verhältnis wie die entsprechenden Abschnitte des zweiten Strahles.
2. Strahlensatz: Wird ein Zweistrahl durch zwei parallele Geraden geschnitten, so stehen die Parallelabschnitte im gleichen Verhältnis, wie die vom Scheitelpunkt aus gemessenen zugehörigen Strahlenabschnitte auf jeweils demselben Strahl.

Körper	Volumen V	Oberfläche O	Bemerkungen, Weiteres
Prismen
Parallelepiped (Spat)	${\displaystyle G\cdot h}$	${\displaystyle 2\cdot (ah_{a}+bh_{b}+ch_{c})}$
Quader	${\displaystyle a\cdot b\cdot c}$	${\displaystyle 2\cdot (ab+ac+bc)}$	Raumdiagonalenlänge ${\displaystyle ={\sqrt {a^{2}+b^{2}+c^{2}}}}$
Allgemeines Prisma	${\displaystyle A_{G}\cdot h}$	${\displaystyle 2A_{G}+A_{M}\,}$	${\displaystyle A_{M}}$ Mantelfläche
Säulen
Rundsäule (Zylinder)	${\displaystyle \pi \cdot r^{2}\cdot h}$	${\displaystyle 2\pi r\cdot (r+h)}$
Hohlzylinder	${\displaystyle \pi R^{2}h-\pi r^{2}h=\,}$ ${\displaystyle \pi h(R+r)(R-r)\,}$	${\displaystyle 2\pi ((R+r)h+R^{2}-r^{2})\,}$	${\displaystyle R,r}$ Außen-,Innenradius ${\displaystyle M_{\text{aussen}}=2\pi Rh}$ ${\displaystyle M_{\text{innen}}=2\pi rh}$
Pyramide
Allgemeine Pyramide	${\displaystyle {\frac {1}{3}}A_{G}h}$	${\displaystyle A_{G}+A_{M}\,}$
Pyramidenstumpf	${\displaystyle {\frac {1}{3}}h\left(A_{G}+{\sqrt {A_{G}A_{D}}}+A_{D}\right)}$	${\displaystyle A_{G}+A_{D}+A_{M}\,}$	${\displaystyle A_{G}}$ Grundfläche ${\displaystyle A_{D}}$ Deckfläche
Kegel
Kreiskegel	${\displaystyle {\frac {1}{3}}\cdot \pi \cdot r^{2}\cdot h}$	nur für senkrechte Kegel: ${\displaystyle r\cdot \pi \cdot (r+s)}$	Zusammenhang von Radius, Höhe und Seitenhöhe: ${\displaystyle s^{2}=r^{2}+h^{2}\,}$
gerader Kegelstumpf	${\displaystyle {\frac {1}{3}}\pi h(r_{1}^{2}+r_{1}r_{2}+r_{2}^{2})}$	${\displaystyle A_{G}+A_{D}+A_{M}\,}$ ${\displaystyle =\pi r_{2}^{2}+\pi r_{1}^{2}+\pi s(r_{1}+r_{2})}$	${\displaystyle s=\mathrm {Mantellinie} ={\sqrt {(r_{2}-r_{1})^{2}+h^{2}}}}$ ${\displaystyle r_{1},r_{2}}$ Radien
Platonische Körper
Tetraeder	${\displaystyle {\frac {1}{12}}a^{3}{\sqrt {2}}}$	${\displaystyle a^{2}{\sqrt {3}}}$
Hexaeder (Würfel)	${\displaystyle a^{3}\,}$	${\displaystyle 6\cdot a^{2}}$	Raumdiagonalenlänge ${\displaystyle =a{\sqrt {3}}}$
Oktaeder	${\displaystyle {\frac {1}{3}}a^{3}{\sqrt {2}}}$	${\displaystyle 2a^{2}{\sqrt {3}}}$
Dodekaeder	${\displaystyle {\frac {1}{4}}a^{3}(15+7{\sqrt {5}})}$	${\displaystyle 3a^{2}{\sqrt {25+10{\sqrt {5}}}}}$
Ikosaeder	${\displaystyle {\frac {5}{12}}a^{3}(3+{\sqrt {5}})}$	${\displaystyle 5a^{2}{\sqrt {3}}}$
Kugel und Kugelteile
Kugel	${\displaystyle {4 \over 3}\cdot \pi \cdot r^{3}={1 \over 6}\cdot \pi \cdot d^{3}}$	${\displaystyle 4\cdot \pi \cdot r^{2}=\pi \cdot d^{2}}$
Kugelkalotte (Kugelmütze, Kugelkappe)		${\displaystyle 2\cdot r\cdot \pi \cdot h}$
Kugelsegment (Kugelabschnitt)	${\displaystyle {h^{2}\cdot \pi \over 3}\cdot (3r-h)}$	${\displaystyle 2\cdot r\cdot \pi \cdot h+\rho ^{2}\pi }$	mit ${\displaystyle \rho ^{2}=h\cdot (2r-h)}$
Kugelzone (Kugelschicht)	${\displaystyle {\frac {1}{6}}\pi \cdot h(3\cdot a^{2}+3\cdot b^{2}+h^{2})}$	${\displaystyle \pi \cdot (2\cdot r\cdot h+a^{2}+b^{2})}$	mit ${\displaystyle 2\cdot a}$ = Durchmesser des unteren Schnittkreises und ${\displaystyle 2\cdot b}$ = Durchmesser des oberen Schnittkreises
Drehkörper
Ellipsoid	${\displaystyle {\frac {4}{3}}\cdot \pi \cdot a\cdot b\cdot c\,}$		Halbachsen a,b,c
Torus	${\displaystyle 2\pi ^{2}\cdot R\cdot r^{2}}$	${\displaystyle 4\pi ^{2}\cdot R\cdot r}$

siehe auch: Eulerscher Polyedersatz, Prinzip von Cavalieri

siehe: Trigonometrie, Formelsammlung Trigonometrie

siehe: Analytische Geometrie, Formelsammlung analytische Geometrie

• Lothar Papula: Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler. mit zahlreichen Rechenbeispielen und einer ausführlichen Integraltafel. 11. überarb. Auflage. Wiesbaden 2014, ISBN 978-3-8348-1913-0. 

1. ↑ Papula: Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler. 2014, S. 28. 
2. ↑ ^{a b} Papula: Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler. 2014, S. 26.