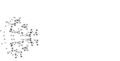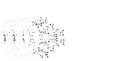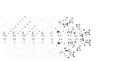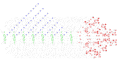|
Zellulärer Automat Zelluläre oder auch zellulare Automaten dienen der Modellierung räumlich diskreter dynamischer Systeme. Sie bestehen aus einzelnen Zellen, die zu diskreten Zeitpunkten gleichzeitig ihren Zustand ändern. Die Änderung erfolgt für alle Zellen nach den gleichen Regeln. Sie hängt von den Zellzuständen in einer vorgegebenen Nachbarschaft und vom Zustand der Zelle selbst ab. Häufig sind die Zellen in einem regelmäßigen Gitter angeordnet (Gittermodell). EigenschaftenEin zellulärer Automat ist durch folgende Größen festgelegt:
Der Zellularraum besitzt eine gewisse Dimensionalität, er ist in der Regel ein- oder zweidimensional, kann aber durchaus auch höherdimensional sein. Man beschreibt das Aussehen eines zellulären Automaten durch eine globale Konfiguration, welche eine Abbildung aus dem Zellularraum in die Zustandsmenge ist, das heißt, man ordnet jeder Zelle des Automaten einen Zustand zu. Der Übergang einer Zelle von einem Zustand (lokale Konfiguration) in den nächsten wird durch Zustandsübergangsregeln definiert, die deterministisch oder stochastisch sein können. Die Zustandsübergänge erfolgen für alle Zellen nach derselben Überführungsfunktion und gleichzeitig. Die Zellzustände können wie die Zeitschritte diskret sein. In der Regel ist die Anzahl der möglichen Zustände klein: Nur wenige Zustandswerte reichen zur Simulation selbst hochkomplexer Systeme aus. Bei zweidimensionalen zellulären Automaten unterscheidet man zwei verschiedene Nachbarschaften: Ähnlich wie bei Monte-Carlo-Simulationen spielen Randbedingungen wie z. B. periodische Randbedingungen eine wichtige Rolle für die Bestimmung der Nachbarn und die Eigenschaften des Modells. Der einfachste zelluläre Automat ist eindimensional, mit Zellen auf einer geraden Linie, wobei jede Zelle nur zwei mögliche Zustände haben kann, z. B. schwarz und weiß. In einem zweidimensionalen Raum sind Quadrate, Sechsecke und Würfel übliche Zellformen. Theoretisch kann ein zellulärer Automat beliebig viele Dimensionen haben und jede Zelle kann beliebig viele mögliche Zustände haben. Der Zustand jeder Zelle ändert sich in diskreten Schritten und in regelmäßigen Zeitintervallen. Dieser Zustand hängt zu jedem Zeitpunkt ab von
Wenn eine grafische Darstellung eines solchen Automaten betrachtet wird, sieht er wie ein gerastertes animiertes Objekt aus.[2] Für einen eindimensionalen zellulären Automat sind 28 = 256 verschiedene Regeln (Überführungsfunktionen) möglich, denn für jeden der 23 = 8 Zustände einer Zelle und ihrer zwei Nachbarzellen (3 benachbarte Zellen) sind unabhängig voneinander 2 neue Zustände möglich.[3][4] GeschichteZellularautomaten wurden um 1940 von Stanislaw Ulam in Los Alamos vorgestellt. John von Neumann, ein damaliger Kollege Ulams, griff die Idee auf und erweiterte sie zu einem universellen Berechnungsmodell. Er stellte einen Zellularautomaten mit 29 Zuständen vor, der ein gegebenes Muster immer wieder selbst reproduzieren kann. Er beschrieb damit als erster einen Zellularautomaten, der berechnungs- und konstruktionsuniversell ist. Er ist nach von Neumann für Probleme biologischer Organisation, Selbstreproduktion und der Evolution von Komplexität geeignet. Damit ist der Zellularautomat auch eine wichtige Grundlage für künstliches Leben. Bis zu den 1960er Jahren waren die Analogrechner den Digitalrechnern bei einigen Fragestellungen überlegen. Ein analoger Zellulärer Automat zur Simulation von Grundwasserströmungen wird im Artikel Analogrechner, Abschnitt „Beispiel: Zellulärer Automat“ genauer beschrieben. In den 1970er Jahren erlangte John Horton Conways Game of Life Berühmtheit. 1969 veröffentlichte Konrad Zuse sein Buch „Rechnender Raum“, worin er annimmt, dass die Naturgesetze diskreten Regeln folgen und das gesamte Geschehen im Universum das Ergebnis der Arbeit eines gigantischen Zellularautomaten sei. 1983 veröffentlichte Stephen Wolfram eine Reihe von grundlegenden Arbeiten zu Zellularautomaten und 2002 das Buch A New Kind of Science. KlassifikationStephen Wolfram definiert in A New Kind of Science und in etlichen Arbeiten aus der Mitte der 1980er Jahre vier Klassen, in die man die zellulären Automaten und ihre Überführungsfunktionen je nach ihrem Verhalten unterteilen kann. Frühere Autoren versuchten lediglich, die Art der Muster für bestimmte Vorschriften zu ermitteln. Dem Aufwand nach geordnet waren dies die Klassen:
Stephen Wolfram vermutete, dass nicht alle zellulären Automaten der Klasse 4 dazu imstande seien, universelle Berechnungen auszuführen. Die Universalität hat sich vor allem für die Regel 110 und Conways Spiel des Lebens bestätigt. Zelluläre Automaten der Klasse 4 haben besondere Eigenschaften. Aus Regel 110 entstehen regelmäßige Muster, die aber nicht so regelmäßig sind wie in Regel 108, sowie ein chaotisches Verhalten, das aber nicht so chaotisch ist wie in Regel 90. Wenn die Zustände der Zellen als boolesche Werte dargestellt werden, kann man die Regeln für eindimensionale zelluläre Automaten in einfacher Form darstellen. Ist der Zustand der Zelle mit dem Index zum Zeitpunkt , dann lässt sich der Zustand auf einfache Weise als dreiwertige boolesche Funktion darstellen. Die Parameter sind die Zustände der Zelle und der zwei Nachbarzellen im vorherigen Schritt:
Für Regel 30, Regel 90 und Regel 110 zum Beispiel erhält man folgende konkrete Überführungsfunktionen:[3] Eine grundlegende Eigenschaft, die ein zellulärer Automaten der Klasse 4 haben muss, ist, dass die Überführungsfunktion lokale, stabile und nichtperiodische Konfigurationen von Zellen hervorbringt, die ihre Form erhalten können. Diese Konfigurationen können als Codierungspakete mit Informationen angesehen werden, die über die Zeit erhalten bleiben und sich von einem Ort zum anderen bewegen. Diese Informationen können sich zeitlich und räumlich ausbreiten, ohne zu zerfallen. Es ist es ein wichtiges Merkmal der universellen Berechnung, ob ein bestimmter Algorithmus bei einer bestimmten Eingabe anhält oder nicht. Die Unentscheidbarkeit des Halteproblems bedeutet, dass man dies im Allgemeinen nicht vorhersagen kann. Aufgrund dieser Erkenntnisse vermutete Stephen Wolfram, dass die zellulären Automaten der Klasse 4 die einzigen seien, die zur universellen Berechnung in der Lage sind. Wenn man die anfängliche Konfiguration eines solchen Automaten als Eingabedaten interpretiert, kann dieser Automat jede berechenbare Funktion bewerten und eine universelle Turingmaschine emulieren.[5] MusterZelluläre Automaten erzeugen Muster, die klassifiziert werden können. Im zweidimensionalen Fall sind das zum Beispiel
Wolframs eindimensionales Universum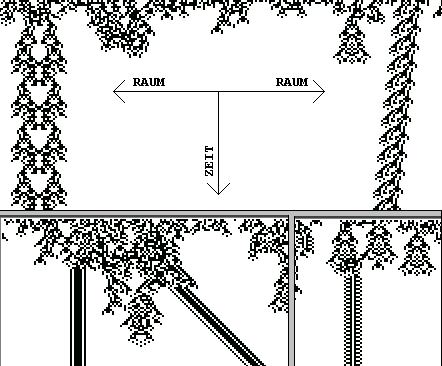 Stephen Wolframs zellulärer Automat ist ein besonders einfaches Modell-Universum. Es besteht aus nur einer Raum- und einer Zeitdimension. Im Bild ist die Raumdimension waagerecht eingezeichnet und die Zeitdimension verläuft senkrecht nach unten. (Das Bild enthält drei verschiedene Bildausschnitte.) Die Raumdimension ist endlich, aber unbegrenzt, denn ihr rechtes und linkes Ende sind topologisch miteinander verbunden (periodische Randbedingungen). Die Raum-Zeit-Elemente dieses Universums können nur leer oder voll sein. Beim „Urknall“ (in den obersten Bildzeilen) werden diese Raum-Zeit-Elemente mit 50-prozentiger Wahrscheinlichkeit gefüllt. Es gibt nur ein Naturgesetz, das eine Nahwirkung darstellt. Der Nahbereich umfasst die linken zwei Nachbarn eines Raum-Zeit-Elements, das Raum-Zeit-Element selbst, und die rechten zwei Nachbarn des Raum-Zeit-Elements. Wenn zwei oder vier Raum-Zeit-Elemente im Nahbereich voll sind, dann ist im nächsten Zeitintervall dieses Raum-Zeit-Element auch voll, ansonsten ist es im nächsten Zeitintervall leer. Es existieren keine weiteren Regeln.
Obwohl es im Gegensatz zu Computer-Spielen keine Fernwirkung und keinerlei Kontrollinstanz gibt, entwickelt sich dieses Modelluniversum zu verblüffender Komplexität. Nach dem „Urknall“ findet eine Eliminationsphase statt, ähnlich wie im echten Universum. Danach entstehen kurzlebige, aber geordnete Strukturen, die irgendwann erlöschen. Einige der geordneten Strukturen sind aber langzeitstabil, manche davon oszillieren, andere davon sind in der Zeit formstabil. Sowohl von den oszillierenden als auch von den formstabilen Strukturen existieren sowohl ortsfeste als auch bewegliche Arten. Die maximale Austauschgeschwindigkeit dieses Universums kann nur zwei Raumeinheiten je Zeiteinheit betragen. Wenn zwischen den stabilen bewegten Objekten Kollisionen stattfinden, dann setzt wieder Chaos ein, und eine weitere Eliminationsphase findet statt. Vereinfacht man noch weiter und berücksichtigt neben dem Zustand des Elementes selbst nur jeweils das rechte und das linke Nachbarelement, gibt es genau 8 Regelelemente. Ein Beispiel dazu steht weiter unten. Insgesamt gibt es 256 solcher Regeln. Selbst unter diesen noch einfacheren Regeln zeigen einige eine erstaunliche Komplexität. Eine der interessantesten ist die „Regel 110“: Regel 110
Siehe auch: Regel 30 Beispiele für zelluläre Automaten
Garten Eden und ZwillingeDer Garten Eden ist eine Konfiguration (Muster) des zellulären Automaten, die keine Vorläufer hat. Sie enthält mindestens eine endliche Konfiguration, die ebenfalls keine Vorläufer hat, einen Waisen (englisch orphan). Ein Zwilling einer endlichen Konfiguration ist eine andere endliche Konfiguration, die die gleichen zukünftigen Muster hat. Ein zellulärer Automat ist injektiv, falls unterschiedliche Teile des Musters auch in Zukunft unterschiedlich bleiben, lokal injektiv, falls keine Zwillinge vorhanden sind, und surjektiv, wenn jede Konfiguration einen Vorläufer hat. Edward F. Moore (1962[7]) und John Myhill (1963[8]) bewiesen den Garten-Eden-Satz in der Theorie zellulärer Automaten: Ein zellulärer Automat im euklidischen Raum ist lokal injektiv genau dann, wenn er surjektiv ist. Das lässt sich auch so ausdrücken, dass zelluläre Automaten genau dann einen Garten Eden haben, wenn sie keine Zwillinge haben. Dabei bewies Moore einen Teil der Äquivalenz (Automaten mit Zwillingen haben Waisen), Myhill die Umkehrung (ein Automat mit Waisen hat auch Zwillinge). AnwendungenBildverarbeitungBildverarbeitung muss in der Lage sein, die Komponenten des Bildes unabhängig von ihrer Position und Drehung zu erkennen, und es sollte auch gegenüber kleinen Unterschieden tolerant sein. Sie sollte ähnliche Strukturen erkennen und ein quantitatives Ergebnis dafür zurückgeben.[9] Viele Bildverarbeitungsprogramme werden mit zellulären Automaten realisiert. Es gibt viele Systeme, die ein sogenanntes Attraktor-Verhalten haben. Als Veranschaulichung kann man Berge verwenden. Ein Tropfen Regen kann überall in den Bergen fallen, aber – in einem idealisierten Modell – fließt es zu einer begrenzten Anzahl von niedrigsten Punkten. Nahe beieinander liegende Tropfen fließen tendenziell zum gleichen niedrigsten Punkt. Tropfen auf der anderen Seite einer Wasserscheide fließen zu anderen niedrigsten Punkten. Bilder bestehen jedoch aus digitalen Pixeln. Anstatt eine physische Bewegung zu betrachten, muss man digitale Werte betrachten, die von Computerprogrammen verarbeitet werden. Ein ähnliches Attraktor-Verhalten kann dort auftreten. Zum Beispiel gibt es viele zelluläre Automaten, bei denen man die Farben einiger Zellen in ihren Anfangszuständen ändern kann, aber immer noch in demselben festen Endzustand endet.[10] Die integrierte Bildverarbeitung von Stephen Wolfram in Mathematica ist ein leistungsstarkes und präzises Instrument zur Erkennung und quantitativen Beschreibung morphologischer Komponenten. Wolfram Research bietet integrierte Unterstützung sowohl für die automatisierte als auch für die interaktive Bildverarbeitung, die vollständig in die leistungsstarken mathematischen und algorithmischen Funktionen der Wolfram-Sprache integriert ist. Sie können Bilder erstellen und importieren, sie mit eingebauten Funktionen manipulieren, lineare und nichtlineare Filter anwenden und auf verschiedene Weise visualisieren.[11] KryptografieEinige kryptographische Verfahren basieren auf zellulären Automaten. Zelluläre Automaten wurden von Guan und Kari für asymmetrische Kryptosysteme vorgeschlagen. Für solche Systeme sind zwei Schlüssel erforderlich: ein öffentlicher Schlüssel für die Verschlüsselung, und ein geheimer privater Schlüssel für die Entschlüsselung. Auch symmetrische Kryptosysteme können mit zellulären Automaten realisiert werden. Der Verschlüsselungsprozess basiert dort auf der Generierung pseudozufälliger Bitfolgen.[12] Künstliches LebenIm Bereich des künstlichen Lebens wird versucht, lebensechte Computermodelle zu schaffen, die Ideen aus dem biologischen Leben übernehmen, beispielsweise dezentrale und lokale Steuerung. Die bei der künstlichen Entwicklung angewandten Techniken basieren häufig auf der indirekten Kodierung von Entwicklungsregeln analog zum Genom eines biologischen Organismus. Diese Art der Kodierung erleichtert die Skalierung eines Organismus, da die Informationen im Genom viel kleiner sind als im resultierenden Phänotyp. Eines der einfachsten Computermodelle für künstliches Leben ist ein zellulärer Automat. Im Jahr 2002 wurde eine zellulärer Automat mit Regeln beschrieben, die durch ein künstliches neuronales Netzwerk definiert werden. Heutzutage wird diese Art von Ansatz als neuronaler zellulärer Automat (NCA) bezeichnet. Im Jahr 2017 haben Forscher einen NCA präsentiert, der Eigenschaften hat, die durch Neuroevolution mit sogenanntem Compositional Pattern-Producing Network erlernt wurden. Im Jahr 2020 haben Forscher einen differenzierbaren NCA entwickelt, der Wachstumseigenschaften und Regenerationseigenschaften besitzt. Bei ihrer Arbeit wird ein NCA mit einem Gradientenverfahren darauf trainiert, aus einer aktiven Zelle ein farbiges Bild zu erzeugen.[13] RobotikFormationen oder Schwärme von Robotern, die bei Rettungsaktionen, bei der Landschaftsvermessung oder im Krieg eingesetzt werden, können mithilfe von zellulären Automaten gesteuert werden. Dabei werden Roboter als Zellen in einem zellularen Automaten modelliert. Das Verhalten jedes einzelnen Roboters ist reaktiv gegenüber seinen Nachbarn und sorgt so für Ordnung in der gesamten Gruppe. Jeder Roboter muss lediglich seine relative Position und Ausrichtung zu jedem Roboter in seiner Nachbarschaft kennen, um einen Bewegungspfad zu berechnen und seine gewünschte Position zu erreichen. Somit wird eine Formation mithilfe einer verteilten Steuerungsarchitektur aufgebaut und aufrechterhalten, die kein globales Informationssystem und keinen zentralen Anführer erfordert.[14] Das Schwarmverhalten von Menschen wird aufgrund ihrer breiten Anwendbarkeit untersucht. Die Analyse eines Schwarms unter unsicheren Bedingungen ist relevant, weil Fußgänger bei Fluchtversuchen manchmal schlimme Fehler machen. Bei solchen Untersuchungen werden Simulationen anhand von Umgebungsabstraktionen strukturiert und die Ergebnisse helfen dabei, Sicherheitsstandards für Gebäude zu bestimmen. Ein weiteres Forschungsgebiet, das mit diesem Ziel in Einklang steht, ist die Untersuchung von mobilen Schwärmen von Robotern. Beispiele für ein solches natürliches kollektives Verhalten sind die Pheromon-Interaktion, die von Ameisenvölkern eingesetzt wird, und der Schwänzeltanz der Bienen. Mehrere von der Biologie inspirierte Algorithmen der Schwarmintelligenz wurden im Kontext der kollektiven Robotik untersucht. Aus der Analyse früherer Studien zur Evakuierung von Menschenmengen konnte eine Parallele zwischen der Dynamik von Fußgängern in Umgebungen mit begrenzter Leistung und dem Verhalten eines Roboterteams bei der Durchführung von Nahrungssuche-Aufgaben gezogen werden. Darüber hinaus sollten Konflikte zwischen dem Roboter und der Umgebung kontrolliert werden, eine ähnliche Situation wie Konflikte zwischen Menschen und Hindernissen, die ihre ursprüngliche Route ändern können. Bei der Simulation von Fußgängern besteht das Ziel darin, Modelle zu finden, die das natürliche Verhalten der Menschenmenge während eines Evakuierungsszenarios nachbilden. Andererseits können in der Robotik ähnliche Modelle zur Steuerung des Roboterverhaltens verwendet werden, was zu einer effizienten Ausführung der Aufgabe führt.[15] PhysikMan kann das Universum als eine riesige numerische Berechnung betrachten, die auf einer Art zellulärem Automaten läuft. Ein Großteil der Schwierigkeiten beim Verständnis von Raum und Zeit in der modernen Physik beruht auf der Annahme, dass Raum und Zeit tatsächlich grundlegende Einheiten in unserem Universum sind. In der Theorie der zellulären Automaten ist dies definitiv nicht der Fall. Raum und Zeit sind das Ergebnis komplexer Wechselwirkungen von Teilchen. Um Materie zu erforschen, muss man Teilchen nutzen, um Teilchen zu untersuchen. Zelluläre Automaten können verwendet werden, um Wechselwirkungen von Teilchen zu simulieren. Es gibt spezielle Computer mit einer Architektur für zelluläre Automaten, die für physikalische Modellierungen und Simulationen eingesetzt werden. Im Gegensatz zu gewöhnlichen Computern aktualisieren solche Computer alle ihre Speicherplätze in einem einzigen Taktzyklus, wodurch sie wesentlich schneller und leistungsfähiger sind. Es ist wichtig zu beachten, dass der Taktzyklus Ereignisse im Zusammenhang mit dem zellulären Automaten markiert und keine Ereignisse in unserem Zeitmaß.[16] Probabilistische Zelluläre AutomatenBei probabilistischen zellulären Automaten sind die Regeln mit denen Übergänge erfolgen nicht deterministisch, sondern zufällig. In diesem Aspekt ähneln probabilistische zelluläre Automaten den Monte-Carlo-Simulationen. Probabilistische zelluläre Automaten stehen im Gegensatz zu deterministischen zellulären Automaten. Ein Beispiel für einen deterministischen Zellulären Automaten ist der Q2R Automat, der das Ising-Modell der theoretischen Physik beschreibt. Der Q2R Automat ist deterministisch, reversibel und sehr schnell. Es wurde allerdings gezeigt, dass der Metropolis-Algorithmus, der auf Zufallsvariablen und Zufallszahlen basiert, geeigneter ist, das Ising-Modell zu beschreiben.[17] Siehe auch
Literatur
WeblinksCommons: Cellular automata – Sammlung von Bildern, Videos und Audiodateien
Sekundärliteratur
Visualisierungen und Implementierungen
Einzelnachweise
|
|||||||||||||||||||||||||||||||||||||||