|
Borda count
The Borda method or order of merit is a positional voting rule that gives each candidate a number of points equal to the number of candidates ranked below them: the lowest-ranked candidate gets 0 points, the second-lowest gets 1 point, and so on. The candidate with the most points wins. The Borda count has been independently reinvented several times, with the first recorded proposal in 1435 being by Nicholas of Cusa (see History below),[1][2] but is named after the 18th-century French mathematician and naval engineer Jean-Charles de Borda, who devised the system in 1770.[3] The Borda count is well-known in social choice theory both for its pleasant theoretical properties and its ease of manipulation. In the absence of strategic voting and strategic nomination, the Borda count tends to elect broadly-acceptable options or candidates (rather than consistently following the preferences of a majority);[4] when both voting and nomination patterns are completely random, the Borda count generally has an exceptionally high social utility efficiency.[5] However, the method is highly vulnerable to spoiler effects when there are clusters of similar candidates; because the effects of more candidates on the election are unbounded, it is possible for any political party to win an election by running enough clones.[5][6] Common implementations of equal-rank or truncated ballots can also incentivize extreme burial when voters are strategic, which allows deeply unpopular dark horse candidates to win by avoiding any attention.[7][8][9] The traditional Borda method is currently used to elect two ethnic minority members of the National Assembly of Slovenia,[10] in modified forms to determine which candidates are elected to the party list seats in Icelandic parliamentary elections,[citation needed] and for selecting presidential election candidates in Kiribati.[11] A variant known as the Dowdall system is used to elect members of the Parliament of Nauru.[12] Until the early 1970s, another variant was used in Finland to select individual candidates within party lists.[citation needed] It is also widely used throughout the world by various private organizations and competitions. The Quota Borda system is a proportional multiwinner variant. Voting and countingBallot The Borda count is a ranked voting system: the voter ranks the list of candidates in order of preference. So, for example, the voter gives a 1 to their most preferred candidate, a 2 to their second most preferred, and so on. In this respect, it is similar to other ranked voting systems such as instant-runoff voting, the single transferable vote or Condorcet methods. The integer-valued ranks for evaluating the candidates were justified by Laplace, who used a probabilistic model based on the law of large numbers. The Borda count is classified as a positional voting system, that is, all preferences are counted but at different values. The other commonly-used positional system is plurality voting, which only assigns one point to the top candidate. Each candidate is assigned a number of points from each ballot equal to the number of candidates to whom he or she is preferred, so that with n candidates, each one receives n – 1 points for a first preference, n – 2 for a second, and so on.[13] The winner is the candidate with the largest total number of points. For example, in a four-candidate election, the number of points assigned for the preferences expressed by a voter on a single ballot paper might be:
Suppose that there are 3 voters, U, V and W, of whom U and V rank the candidates in the order A-B-C-D while W ranks them B-C-D-A.
Thus Brian is elected. A longer example, based on a fictitious election for Tennessee state capital, is shown below. PropertiesElections as estimation proceduresCondorcet looked at an election as an attempt to combine estimators. Suppose that each candidate has a figure of merit and that each voter has a noisy estimate of the value of each candidate. The ballot paper allows the voter to rank the candidates in order of estimated merit. The aim of the election is to produce a combined estimate of the best candidate. Such an estimator can be more reliable than any of its individual components.[14] Peyton Young showed that the Borda count gives an approximately maximum likelihood estimator of the best candidate.[5] His theorem assumes that errors are independent, in other words, that if a voter rates a particular candidate highly, then there is no reason to expect her to rate "similar" candidates highly. If this property is absent – if the voter gives correlated rankings to candidates with shared attributes – then the maximum likelihood property is lost, and the Borda count is highly subject to nomination effects: a candidate is more likely to be elected if there are similar candidates on the ballot. Effect of irrelevant candidates The Borda count is particularly susceptible to distortion through the presence of candidates who do not themselves come into consideration, even when the voters lie along a spectrum. Voting systems which satisfy the Condorcet criterion are protected against this weakness since they automatically also satisfy the median voter theorem, which says that the winner of an election will be the candidate preferred by the median voter regardless of which other candidates stand. Suppose that there are 11 voters whose positions along the spectrum can be written 0, 1, ..., 10, and suppose that there are 2 candidates, Andrew and Brian, whose positions are as shown:
The median voter Marlene is at position 5, and both candidates are to her right, so we would expect A to be elected. We can verify this for the Borda system by constructing a table to illustrate the count. The main part of the table shows the voters who prefer the first to the second candidate, as given by the row and column headings, while the additional column to the right gives the scores for the first candidate.
A is indeed elected. But now suppose that two additional candidates, further to the right, enter the election.
The counting table expands as follows:
The entry of two dummy candidates allows B to win the election. Similar examples led the Marquis de Condorcet to argue that the Borda count is "bound to lead to error" because it "relies on irrelevant factors to form its judgments".[12] Other propertiesThere are a number of formalised voting system criteria whose results are summarised in the following table.
Simulations show that Borda has a high probability of choosing the Condorcet winner when one exists, in the absence of strategic voting and with ballots ranking all candidates.[1][12] Equal ranksSeveral different methods of handling tied ranks have been suggested. They can be illustrated using the 4-candidate election discussed previously.
Effects on strategyThe modified Borda and tournament Borda methods, as well as methods of Borda that do not allow for equal rankings, are well-known for behaving disastrously in response to tactical voting, a reaction called a turkey election.[7] The French Academy of Sciences (of which Borda was a member) experimented with Borda's system but abandoned it, in part because "the voters found how to manipulate the Borda rule".[16] In response to the issue of strategic manipulation in the Borda count, M. de Borda said:[17][16][18]
Despite its abandonment, the rounded-down Borda rule has a substantially less severe reaction to tactical voting than the traditional or tournament variants. Tactical voting consists of the relatively mild bullet voting, which only causes the race to behave like a cross between a plurality vote and an honest Borda count, rather than producing a potential turkey-election. In Slovenia, which uses this form of the rule, roughly 42% of voters rank a second preference.[19] Forced truncationSome implementations of Borda voting require voters to truncate their ballots to a certain length:
Multiple winnersThe system invented by Borda was intended for use in elections with a single winner, but it is also possible to conduct a Borda count with more than one winner, by recognizing the desired number of candidates with the most points as the winners. In other words, if there are two seats to be filled, then the two candidates with most points win; in a three-seat election, the three candidates with most points, and so on. In Nauru, which uses the multi-seat variant of the Borda count, parliamentary constituencies of two and four seats are used. The quota Borda system is a system of proportional representation in multi-seat constituencies that uses the Borda count. Chris Geller's STV-B uses vote count quotas to elect, but eliminates the candidate with the lowest Borda score; Geller-STV does not recalculate Borda scores after partial vote transfers, meaning partial-transfer of votes affects voting power for election but not for elimination.[citation needed] Related systemsNanson's and Baldwin's methods are Condorcet-consistent voting methods based on the Borda score. Both are run as series of elimination rounds analogous to instant-runoff voting. In the first case, in each round every candidate with less than the average Borda score is eliminated; in the second, the candidate with lowest score is eliminated. Unlike the Borda count, Nanson and Baldwin are majoritarian and Condorcet methods because they use the fact that a Condorcet winner always has a higher-than-average Borda score relative to other candidates, and the Condorcet loser a lower than average Borda score.[22] However they are not monotonic. Potential for tactical manipulationBorda counts are vulnerable to manipulation by both tactical voting and strategic nomination. The Dowdall system may be more resistant, based on observations in Kiribati using the modified Borda count versus Nauru using the Dowdall system,[11] but little research has been done thus far on the Nauru system. Tactical votingBorda counts are unusually vulnerable to tactical voting, even compared to most other voting systems.[23] Voters who vote tactically, rather than via their true preference, will be more influential; more alarmingly, if everyone starts voting tactically, the result tends to approach a large tie that will be decided semi-randomly. When a voter utilizes compromising, they insincerely raise the position of a second or third choice candidate over their first choice candidate, in order to help the second choice candidate to beat a candidate they like even less. When a voter utilizes burying, voters can help a more-preferred candidate by insincerely lowering the position of a less-preferred candidate on their ballot. Combining both these strategies can be powerful, especially as the number of candidates in an election increases. For example, if there are two candidates whom a voter considers to be the most likely to win, the voter can maximise his impact on the contest between these front runners by ranking the candidate whom he likes more in first place, and ranking the candidate whom he likes less in last place. If neither front runner is his sincere first or last choice, the voter is employing both the compromising and burying tactics at once; if enough voters employ such strategies, then the result will no longer reflect the sincere preferences of the electorate. For an example of how potent tactical voting can be, suppose a trip is being planned by a group of 100 people on the East Coast of North America. They decide to use Borda count to vote on which city they will visit. The three candidates are New York City, Orlando, and Iqaluit. 48 people prefer Orlando / New York / Iqaluit; 44 people prefer New York / Orlando / Iqaluit; 4 people prefer Iqaluit / New York / Orlando; and 4 people prefer Iqaluit / Orlando / New York. If everyone votes their true preference, the result is:
If the New York voters realize that they are likely to lose and all agree to tactically change their stated preference to New York / Iqaluit / Orlando, burying Orlando, then this is enough to change the result in their favor:
In this example, only a few of the New York voters needed to change their preference to tip this result because it was so close – just five voters would have been sufficient had everyone else still voted their true preferences. However, if Orlando voters realize that the New York voters are planning on tactically voting, they too can tactically vote for Orlando / Iqaluit / New York. When all of the New York and all of the Orlando voters do this, however, there is a surprising new result:
The tactical voting has overcorrected, and now the clear last place option is a threat to win, with all three options extremely close. Tactical voting has entirely obscured the true preferences of the group into a large near-tie. Strategic nominationThe Borda count is highly vulnerable to a form of strategic nomination called teaming or cloning. This means that when more candidates run with similar ideologies, the probability of one of those candidates winning increases. This is illustrated by the example 'Effect of irrelevant alternatives' above. Therefore, under the Borda count, it is to a faction's advantage to run as many candidates as it can. For example, even in a single-seat election, it would be to the advantage of a political party to stand as many candidates as possible in an election. In this respect, the Borda count differs from many other single-winner systems, such as the 'first past the post' plurality system, in which a political faction is disadvantaged by running too many candidates. Under systems such as plurality, 'splitting' a party's vote in this way can lead to the spoiler effect, which harms the chances of any of a faction's candidates being elected. Strategic nomination is used in Nauru, according to MP Roland Kun, with factions running multiple "buffer candidates" who are not expected to win, to lower the tallies of their main competitors.[12] However, the effect of this strategic nomination is greatly reduced by the use of a harmonic progression rather than a simple arithmetic progression. Because the harmonic series is unbounded, it is theoretically possible to elect any candidate (no matter how unpopular) by nominating enough clones. In practice, the number of clones required to do so would likely exceed the total population of Nauru. Example
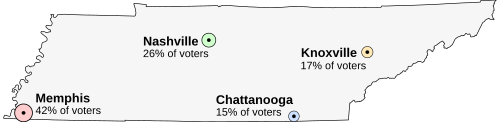
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
The preferences of each region's voters are:
Accordingly Nashville is elected. DowdallUnder Dowdall rules the table would be as follows
Just like normal Borda rules, Nashville would win. Current usesPolitical usesThe Borda count is used for certain political elections in Slovenia and the Micronesian nation of Kiribati. A similar rule is used in Nauru. In Slovenia, the Borda count is used to elect two of the ninety members of the National Assembly: one member represents a constituency of ethnic Italians, the other a constituency of the Hungarian minority. Members of the Parliament of Nauru are elected based on a variant of the Borda count that involves two departures from the normal practice:
In Kiribati, the president (or Beretitenti) is elected by the plurality system, but a variant of the Borda count is used to select either three or four candidates to stand in the election. The constituency consists of members of the legislature (Maneaba). Voters in the legislature rank only four candidates, with all other candidates receiving zero points. Since at least 1991, tactical voting has been an important feature of the nominating process. The Republic of Nauru became independent from Australia in 1968. Before independence, and for three years afterwards, Nauru used instant-runoff voting, importing the system from Australia, but since 1971, a variant of the Borda count has been used. The modified Borda count has been used by the Green Party of Ireland to elect its chairperson.[24][25] The Borda count has been used for non-governmental purposes at certain peace conferences in Northern Ireland, where it has been used to help achieve consensus between participants including members of Sinn Féin, the Ulster Unionists, and the political wing of the UDA.[citation needed] Other usesThe Borda count is used in elections by some educational institutions in the United States:
The Borda count is used in elections by some professional and technical societies:
The OpenGL Architecture Review Board uses the Borda count as one of the feature-selection methods. The Borda count is used to determine winners for the World Champion of Public Speaking contest organized by Toastmasters International. Judges offer a ranking of their top three speakers, awarding them three points, two points, and one point, respectively. All unranked candidates receive zero points. The modified Borda count is used to elect the President for the United States member committee of AIESEC. The Eurovision Song Contest uses a heavily modified form of the Borda count, with a different distribution of points: only the top ten entries are considered in each ballot, the favorite entry receiving 12 points, the second-placed entry receiving 10 points, and the other eight entries getting points from 8 to 1. Although designed to favor a clear winner, it has produced very close races and even a tie. The Borda count is used for wine trophy judging by the Australian Society of Viticulture and Oenology, and by the RoboCup autonomous robot soccer competition at the Center for Computing Technologies, in the University of Bremen in Germany. The Finnish Associations Act lists three different modifications of the Borda count for holding a proportional election. All the modifications use fractions, as in Nauru. A Finnish association may choose to use other methods of election, as well.[27] Sports awardsThe Borda count is a popular method for granting sports awards. American uses include:
In information retrievalThe Borda count has been proposed as a rank aggregation method in information retrieval, in which documents are ranked according to multiple criteria and the resulting rankings are then combined into a composite ranking. In this method, the ranking criteria are treated as voters, and the aggregate ranking is the result of applying the Borda count to their "ballots".[29] Analogy with sporting tournamentsSporting tournaments frequently seek to produce a ranking of competitors from pairwise matches, in each of which a single point is awarded for a win, half a point for a draw, and no points for a loss. (Sometimes the scores are doubled as 2/1/0.) This is analogous to a Borda count in which each preference expressed by a single voter between two candidates is equivalent to a sporting fixture; it is also analogous to Copeland's method supposing that the electorate's overall preference between two candidates takes the place of a sporting fixture. This scoring system was adopted for international chess around the middle of the nineteenth century and by the English Football League in 1888–1889. HistoryThe Borda count is thought to have been developed independently at least four times:
See also
Notes
References
Works cited
Further reading
External links
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||