Cauchy's integral theorem
|

Samsung Galaxy S20 Fan EditionMerekSamsung GalaxyPembuatSamsung ElectronicsSeriGalaxy SJaringan2G, 3G, 4G, 4G LTE, 5GRilis pertama2 Oktober 2020; 3 tahun lalu (2020-10-02)PendahuluSamsung Galaxy S10 LiteTerkaitSamsung Galaxy S20Samsung Galaxy Note 20TipeSmartphoneFaktor bentukSlateDimensi1.598 mm × 745 mm × 84 mm (62,9 in × 29,3 in × 3,3 in)Berat190 g (6,7 oz)Sistem OperasiOriginal: Android 10 with One UI 2.5 Current: Android 1…

Within the Indo-Greek Kingdom there were over 30 kings, often in competition on different territories. Many of them are only known through their coins. Many of the dates, territories, and relationships between Indo-Greek kings are tentative and essentially based on numismatic analysis (find places, overstrikes, monograms, metallurgy, styles), a few Classical writings, and Indian writings and epigraphic evidence. The following list of kings, dates and territories after the reign of Demetrius is d…
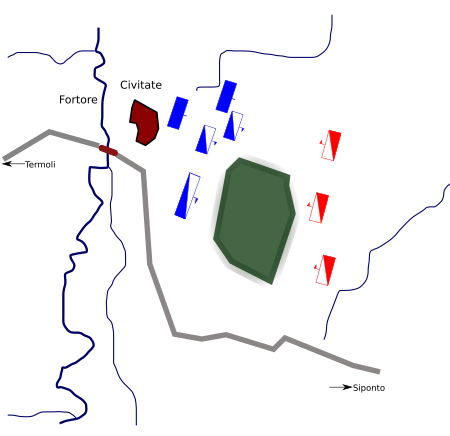
Pertempuran CivitatePeta Pertempuran Civitate.Merah: Norman. Biru: koalisi Paus.Tanggal18 Juni 1053LokasiCivitella del Fortore (dekat Foggia), ItaliaHasil Kemenangan NormanPihak terlibat Norman Koalisi PausOrang Schwaben, Italia, LangobardiTokoh dan pemimpin Humphrey dari HautevilleRobert GuiscardRichard Drengot Rudolf dari BeneventoGerard, Adipati LorraineKekuatan 3.000 pasukan berkudaSekitar 500 infantri Sekitar 6.000 infantri dan pasukan berkuda Pertempuran Civitate (juga dikenal dengan nama …

2016 filmNanna Ninna Prema KatheDirected byShivu JamkhandiWritten byShivu JamkhandiProduced byAnand S NamagoudaStarringVijay Raghavendra Nidhi Subbaiah Thilak ShekarCinematographyMohammad HaseebEdited byDamador KanasooruMusic byShivu JamkhandiProductioncompanyAB Cinema CreationsRelease date 15 July 2016 (2016-07-15) LanguageKannada Nanna Ninna Prema Kathe is a 2016 Indian Kannada romantic drama film directed by Shivu Jamkhandi and produced by actor Anand S. Namagouda. The film sta…

Serangan Dorylus Afrika Nama semut tentara (atau semut legiun atau marabunta [1] ) diterapkan pada lebih dari 200 spesies semut dalam garis keturunan berbeda. Karena kelompok predatornya yang agresif mencari makan, yang dikenal sebagai serangan, sejumlah besar semut mencari makan secara bersamaan di wilayah terbatas. Ciri umum lainnya adalah, tidak seperti kebanyakan spesies semut, semut tentara tidak membangun sarang permanen; sebuah koloni semut tentara bergerak hampir tanpa henti sepa…

Mariana dari AustriaLukisan karya VelázquezPermaisuri SpanyolPeriode7 Oktober 1649 – 17 September 1665Informasi pribadiKelahiran(1634-12-24)24 Desember 1634Wiener Neustadt, Kadipaten Utama Austria, Kekaisaran Romawi SuciKematian16 Mei 1696(1696-05-16) (umur 61)Istana Uceda, Madrid, SpanyolPemakamanEl EscorialWangsaHabsburgNama lengkapMaria AnnaAyahFerdinand III, Kaisar Romawi SuciIbuMaria Anna dari SpanyolPasanganFelipe IV dari SpanyolAnakMargarita Teresa, Maharani Romawi SuciInfanta Mar…

The Montenegrin Footballer of the Year is an annual award chosen by the team captains and the coaches of the Prva crnogorska fudbalska liga — 1. CFL to determine the best player in Montenegro. It is published by the Football Association of Montenegro. The most successful player is Mirko Vučinić, who has won the award seven times, as well as being the inaugural winner. Stevan Jovetić is the youngest player to receive this honour so far; he was 20 years old when he won the award. The most rec…

Untuk orang lain dengan nama yang sama, lihat John Reed (disambiguasi). John ReedReed pada sekitar tahun 1915LahirJohn Silas Reed(1887-10-22)22 Oktober 1887Portland, Oregon, Amerika SerikatMeninggal17 Oktober 1920(1920-10-17) (umur 32)Moskwa, Republik Soviet RusiaSebab meninggalScrub typhusMakamKremlin Wall NecropolisKebangsaanAmerikaPendidikanHarvard UniversityPekerjaanJurnalisPartai politikPartai Buruh Komunis AmerikaSuami/istriLouise Bryant (m. 1916;&…

Municipality in Catalonia, SpainLa Vansa i FórnolsMunicipalityFórnols Coat of armsLa Vansa i FórnolsLocation in CataloniaCoordinates: 42°14′7″N 1°29′0″E / 42.23528°N 1.48333°E / 42.23528; 1.48333Country SpainCommunity CataloniaProvince LleidaComarcaAlt UrgellGovernment • MayorJosep Xavier Camps Torrens (2015)[1]Area[2] • Total106.1 km2 (41.0 sq mi)Population (2018)[3] �…

Untuk kegunaan lain, lihat Barcelona (disambiguasi). BarcelonaSearah jarum jam dari atas: Kaki langit Barcelona, La Barceloneta, Camp Nou, Diagonal Mar, Sagrada Familia, dan Castell dels tres Dragons BenderaLambang kebesaranJulukan: Ciutat Comtal (Kota Bangsawan), Barna, BCNNegaraSpanyolKomunitas OtonomCataloniaProvinsiBarcelonaComarcaBarcelonèsDistrikCiutat Vella, Eixample, Gràcia, Horta-Guinardó, Les Corts, Nou Barris, Sant Andreu, Sants–Montjuïc, Sarrià-Sant Gervasi, Sant MartíPe…

Ini adalah nama Melayu; nama Marlias merupakan patronimik, bukan nama keluarga, dan tokoh ini dipanggil menggunakan nama depannya, Farizal. Mohd Farizal Informasi pribadiNama lengkap Mohd Farizal MarliasTanggal lahir 29 Juni 1986 (umur 37)Tempat lahir Makassar, IndonesiaTinggi 1,78 m (5 ft 10 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini Johor Darul Takzim FCNomor 21Karier senior*Tahun Tim Tampil (Gol)2006-2008 Shahzan Muda 37 (0)2009-2010 Perlis 32 (0)2011-2012…
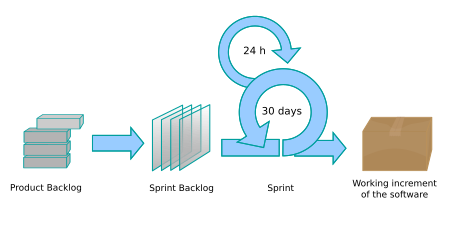
Proses Scrum Scrum adalah metode pengembangan perangkat lunak agile yang dikembangkan oleh Jeff Sutherland dan tim pengembangannya di awal 1990-an. Selanjutnya, pengembangan lebih lanjut tentang metode Scrum telah dilakukan oleh Schwaber dan Beedle.[1] Prinsip scrum konsisten dengan manifesto agile dan digunakan untuk memandu kegiatan pengembangan dalam suatu proses yang menggabungkan kegiatan kerangka kerja (framework activity) berikut: kebutuhan (requirements), analisis (analysis), des…

Mount MycaleΜυκάληSamsun DağiBagian samping Mykale di belakang PrieneTitik tertinggiKetinggian1.237 m (4.058 ft)di Dilek Tepesi, the high point; 600 meter (1.969 ft) averagePenamaanNama terjemahanGunung Samson (bahasa Turki)GeografiMount MycaleProvinsi Aydin, TurkiPegununganAydin Mountain Range in the Menderes MassifGeologiJenis gunungRidge, 200 kilometer (124 mi) longPendakianRute termudahHike Mykale atau Mycali (bahasa Yunani Kuno: Μυκάλη), disetbu Sams…

BongaCamsTangkapan layar Jenis situsSitus web dewasaBahasaMulti-bahasa (34)Wilayah operasiSeluruh dunia, kecuali negara-negara yang memblokirnyaSektorInternetSitus webbongacams.com Peringkat Alexa 35 (June 2020[update])[1]IklanYaDaftar akunOpsionalDiluncurkan25 Januari 2012; 12 tahun lalu (2012-01-25)[2]StatusAktif Portal InternetSunting kotak info • L • BBantuan penggunaan templat ini BongaCams adalah sebuah situs web dewasa yang berbasis di …

Questa voce o sezione sull'argomento editoria non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce è parte della serieGiornalismo Notiziabilità Notizia Regola delle 5 W Verifica dei fatti Rassegna stampa Linea editoriale Stile giornalistico Storia del giornalismo Articoli Titolo Articolo Articolo di …

Questa voce o sezione sull'argomento citologia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Gli organelli di una cellula vegetale Gli organelli di una cellula animale Gli organuli[1] o organelli[2] sono strutture provviste di membrana presenti all'interno della cellula eucariota che svolgon…

Kapal selam kelas Taigei JS Taigei di Pelabuhan Kobe, 9 Maret 2022 Tentang kelas Nama:Kelas TaigeiPembangun:Mitsubishi Heavy IndustriesKawasaki Heavy IndustriesOperator: Angkatan Laut Bela Diri JepangDidahului oleh:Kelas SōryūBiaya:¥69,7 miliar (sekitar $ 635 juta)Dibangun:2018–sekarangBertugas:2022–sekarangRencana:7Aktif:1 Ciri-ciri umum Jenis Kapal selam serbuBerat benaman 3.000 ton (mengapung)Panjang 84 m (276 ft)Lebar 9,1 m (30 ft)Daya muat 10,4 m (34 ft)…

2007 single by Five Finger Death PunchThe BleedingSingle by Five Finger Death Punchfrom the album The Way of the Fist ReleasedJuly 10, 2007GenreAlternative metalLength4:28LabelFirmSongwriter(s) Ivan Moody Zoltan Bathory Producer(s) Zoltan Bathory Jeremy Spencer Five Finger Death Punch singles chronology The Bleeding (2007) Never Enough (2008) Alternative coverUK 7-inch vinyl cover Music videoThe Bleeding on YouTube The Bleeding is a song by American heavy metal band Five Finger Death Punch. It i…

Le Curé de Tours Image from Le Curé de ToursAuthorHonoré de BalzacIllustratorPierre VidalCountryFranceLanguageFrenchSeriesLa Comédie humainePublisherMame-DelaunayPublication date1832Preceded byPierrette Followed byLa Rabouilleuse Le Curé de Tours is a long short story (or, more properly, a novella) by Honoré de Balzac, written in 1832. Originally entitled Les Célibataires (The Celibates), it was published in that year in volume III of the 2nd edition of Scènes de la …

OlševaOlševaHighest pointElevation1,929 m (6,329 ft)Prominence590 m (1,940 ft)[1]Coordinates46°26′59.280″N 14°41′22.920″E / 46.44980000°N 14.68970000°E / 46.44980000; 14.68970000GeographyOlševaLocation in the AlpsShow map of AlpsOlševaOlševa (Slovenia)Show map of Slovenia LocationSloveniaParent rangeKarawanks Mount Olševa (pronounced [ˈoːu̯ʃɛʋa]; German Olschewa) is a ridge mountain in the eastern part of th…










![{\displaystyle \gamma :[a,b]\to U}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d032547cae79cddd62ad7e267d9073b29a5a89d0)


![{\displaystyle \gamma (t)=e^{it}\quad t\in \left[0,2\pi \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8c31ef138b7b9684d8d3572b4c0a8bedfeb5dff)







![{\displaystyle \gamma (t)=e^{it}\quad t\in \left[0,2\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2153454b7e40508bc85b3ff455a8c7a63375fab8)




















