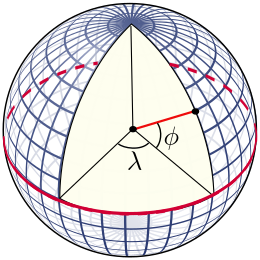
Geographic coordinate system
|
Read other articles:

Seorang penambang batu bara menyelesaikan tinjauan penyaringan untuk paru-paru hitam. Dalam kedokteran, penapisan atau penyaringan (Inggris: screeningcode: en is deprecated ) adalah cara yang digunakan untuk mencari keadaan atau penanda risiko yang belum diketahui.[1][2][3] Pengujian ini dapat diterapkan kepada individu atau seluruh populasi. Orang yang diuji mungkin tidak menunjukkan tanda atau gejala penyakit apa pun atau menunjukkan satu atau dua gejala yang dengan sen…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. GorgaMunisipalitasCarrer Major Lambang kebesaranGorgaLokasi di Provinsi AlicanteTampilkan peta Province of AlicanteGorgaGorga (Spanyol)Tampilkan peta SpanyolKoordinat: 38°43′05″N 0°21′26″W / 38.71806°N 0.35722°W / 38.7180…

Erica acuta Klasifikasi ilmiah Kerajaan: Plantae Divisi: Tracheophyta Kelas: Magnoliopsida Ordo: Ericales Famili: Ericaceae Genus: Erica Spesies: Erica acuta Nama binomial Erica acutaAndrews Erica acuta adalah spesies tumbuhan yang tergolong ke dalam famili Ericaceae. Spesies ini juga merupakan bagian dari ordo Ericales. Spesies Erica acuta sendiri merupakan bagian dari genus Erica.[1] Nama ilmiah dari spesies ini pertama kali diterbitkan oleh Andrews. Referensi ^ Erica Tourn. ex L. Plan…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Kunizo Mori (1890-1949) adalah seorang perwira Angkatan Laut Kekaisaran Jepang atau Kaigun yang bertugas di Makassar, Sulawesi Selatan saat Kekaisaran Jepang menduduki Hindia Belanda (sekarang Indonesia) selama Perang Dunia II.[1] Karier Kunizo M…

Voce principale: Unione Sportiva Sassuolo Calcio. US Sassuolo CalcioStagione 2013-2014Sport calcio Squadra Sassuolo Allenatore Eusebio Di Francesco (1ª-21ª) (27ª-38ª) Alberto Malesani (22ª-26ª) All. in seconda Ezio Sella Presidente Carlo Rossi Serie A17º Coppa ItaliaQuarto turno Maggiori presenzeCampionato: Pegolo, Zaza (33)[1]Totale: Zaza (35) Miglior marcatoreCampionato: Berardi (16)[1]Totale: Berardi (16) StadioStadio Alberto Braglia Abbonati7 795[2] M…

Halaman ini berisi artikel tentang the film. Untuk the original novel by Lois Duncan, lihat I Know What You Did Last Summer. I Know What You Did Last SummerSutradaraJim GillespieProduserWilliam S. BeasleyNeal H. MortizStokely ChaffinDitulis olehKevin WilliamsonPemeranJennifer Love HewittSarah Michelle GellarRyan PhillippeFreddie Prinze, Jr.Penata musikJohn DebneyDistributorColumbia PicturesMandalay PicturesTanggal rilis17 Oktober 1997Durasi100 menitNegara Amerika SerikatBahasaBahasa I…

У этого термина существуют и другие значения, см. Юань. Символы или знаки юаня — традиционные иероглифы (圓, 元) их упрощённые версии (圆, 円), слоги (원) и основанные на латинице графемы (¥, ₩, $), используемые для краткого обозначения юаня и других денежных единиц региона, чьи наз…

SMA Negeri 27 BandungInformasiDidirikan2006JenisSekolah NegeriKepala SekolahHadili M.PdJurusan atau peminatanIPA dan IPSRentang kelasX, XI,XII MIPA, , X, XI,XII IPSKurikulum2013StatusNegeriAlamatLokasiJalan Utsman Bin Affan No. 1 Kel. Rancanumpang Kec. Gedebage, Bandung, Jawa Barat, IndonesiaTel./Faks.(022) 7838362Moto SMA Negeri 27 Bandung, merupakan salah satu Sekolah Menengah Atas Negeri yang ada di Bandung. SMA Negeri 27 Bandung beralamat di Jalan Utsman Bin Affan No. 1 Kel. Ranca…

Jermanofobia beralih ke halaman ini, yang bukan mengenai Jermofobia. Hancurkan monster gila ini—Propaganda Amerika Serikat (Harry R. Hopps; 1917). Poster ini dirilis tahun 1917 oleh Harry Ryle Hopps, menggambarkan Jerman sebagai gorila yang menyerang Amerika Serikat setelah menaklukkan Eropa.[1] Kartun anti-Jerman dari Australia, Norman Lindsay, antara tahun 1914 dan 1918 Poster anti-Jerman dari Britania, sekitar tahun 1919, menyerukan boikot terhadap barang-barang Jerman dan menggamba…

American punk rock band For other uses, see Husker Du (disambiguation). Hüsker DüHüsker Dü in 1986 Left to right: Greg Norton, Grant Hart, and Bob MouldBackground informationOriginSaint Paul, Minnesota, United StatesGenres Hardcore punk post-hardcore punk rock alternative rock Years active1979–1988Labels Reflex Records Alternative Tentacles New Alliance SST Warner Bros. Past members Grant Hart Bob Mould Greg Norton Hüsker Dü (/ˈhʊskər ˈduː/) was an American punk rock band formed in …

City in Ucayali, Peru This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) You can help expand this article with text translated from the corresponding article in Spanish. (August 2010) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations,…

Сирийский бурый медведь Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКлас�…

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Птиц�…

Resolusi 1570Dewan Keamanan PBBSahara BaratTanggal28 Oktober 2004Sidang no.5.068KodeS/RES/1570 (Dokumen)TopikSituasi seputar Sahara BaratRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Aljazair Angola Benin Brasil Chili Spanyol Jerman Pakistan Filipina Rumania Resolusi 1570 De…

Niels VandeputteInformationsNaissance 19 septembre 2000 (23 ans)WestmalleNationalité belgeÉquipe actuelle Alpecin-Deceuninck Development TeamÉquipe non-UCI 2016-2018IKO Enertherm-BKCPÉquipes UCI 2019-7.2020Iko-Crelan8.2020-2020Alpecin-Fenix (stagiaire)2021-6.2022Alpecin-Fenix Development7.2022-Alpecin-Deceuninck Development Teammodifier - modifier le code - modifier Wikidata Niels Vandeputte, né le 19 septembre 2000 à Malle, est un coureur cycliste belge. Spécialiste du cyclo-cross, …

The 2nd Dragoons or 2nd Dragoon Regiment may refer to: 2nd Dragoons, a British regiment usually known as the Royal Scots Greys 2nd Dragoons (Canada), a Canadian regiment that amalgamated into the 2nd/10th Dragoons 2nd Dragoon Regiment (Denmark) 2nd Dragoon Regiment (France) 2nd Cavalry Regiment (United States), also known as the 2nd Dragoons See also 2nd Dragoon Guards (Queen's Bays) 2nd Regiment (disambiguation) Topics referred to by the same termThis disambiguation page lists articles about mi…

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Lepat – berita · surat kabar · buku · cendekiawan · JSTOR Lepat adalah makanan khas Indonesia, yang banyak dijumpai pada masyarakat Sumatra, seperti Minangkabau, Aceh, dan Melayu. Lepat terbuat dari tepung …

Hawker HectorHawker Hector.DescrizioneTipoCooperazione. Equipaggio2 Costruttore Hawker Aircraft Data primo volo14 febbraio 1936 Utilizzatore principale RAF Esemplari179 Sviluppato dalHawker Hart Dimensioni e pesiLunghezza9,09 m (29 ft 9¾ in) Apertura alare11,26 m (36 ft 11½ in) Altezza3,18 m (10 ft 5 in) Superficie alare33,1 m²[1] (346 ft²) Carico alare67,3 kg/m² (14,2 lb/ft²) Peso a vuoto1 537 kg (3 389 lb) Peso carico2 227 kg (4 910 lb) PropulsioneMotore1 Napi…

Historic church in Manhattan, New York United States historic placeFirst Church of Christ, ScientistU.S. Historic districtContributing propertyNew York City Landmark No. LP-0833 Former building of the First Church of Christ, Scientist in Manhattan, New York CityShow map of New York CityShow map of New YorkShow map of the United StatesLocation1 West 96th Street, Manhattan, New York City, New York, United StatesCoordinates40°47′31.2″N 73°57′53.64″W / 40.792000°…

American businessman and inventor (1955–2011) For other uses, see Steve Jobs (disambiguation). Steve JobsJobs introduces the iPhone 4 in 2010.BornSteven Paul Jobs[1](1955-02-24)February 24, 1955San Francisco, California, USDiedOctober 5, 2011(2011-10-05) (aged 56)Palo Alto, California, USResting placeAlta Mesa Memorial ParkEducationReed College (attended)Years active1971–2011Known for Pioneer of the personal computer revolution with Steve Wozniak Co-creator of the Appl…