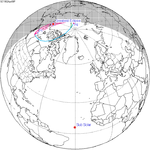
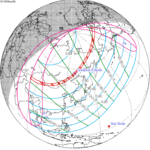
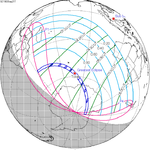
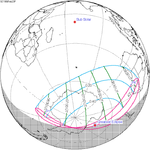
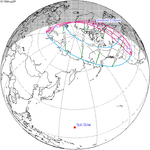
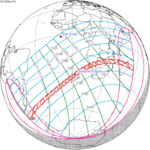
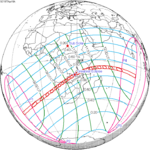
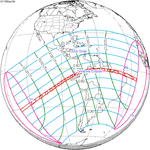
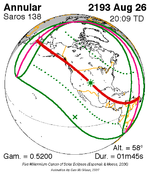
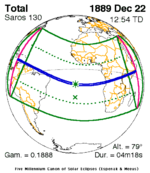
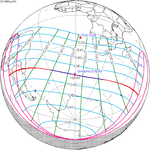
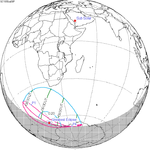
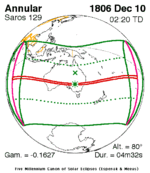
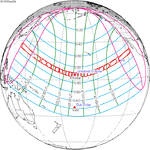
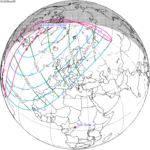
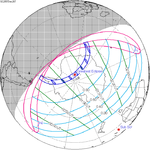
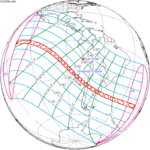
Solar eclipse of March 6, 1905
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Boubacar KeitaInformasi pribadiNama lengkap Boubacar KeitaTanggal lahir 20 Mei 1984 (umur 39)Tempat lahir Conakry, GuineaTinggi 1,86 m (6 ft 1 in)Posisi bermain Bek, gelandangInformasi klubKlub saat ini Kenkre FCNomor 6Karier senior*T…

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен · …

Mira LesmanaMira Lesmana saat wawancara dengan Narasi, September 2020LahirMira Lesmanawati8 Agustus 1964 (umur 59)Jakarta, IndonesiaAlmamaterInstitut Kesenian JakartaPekerjaanProduserpenulis laguTahun aktif1980 - sekarangSuami/istriMathias Muchus (m. 1990)Anak2Orang tuaJack Lesmana (ayah) Nien Lesmana (ibu)KeluargaIndra Lesmana (adik) Eva Celia (keponakan) Lauren Marie-Elizabeth Antariksa (keponakan) Mira Lesmanawati (lahir 8 Agustus 1964) adalah seorang …

Capital and largest city of Transnistria Not to be confused with Terespol. You can help expand this article with text translated from the corresponding article in Russian. (February 2017) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into t…

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of things named after Alexander Hamilton – news · newspapers · books · scholar · JSTOR (December 2022) (Learn how and when to remove this template message) Portrait by John Trumbull, c. 1792 Since the death of Alexander Hamilton on July 12, 1804,[1] n…
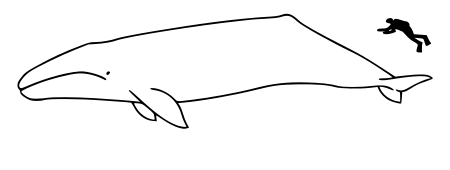
Paus kelabuRentang fosil: Akhir pleistosen–sekarang[1] PreЄ Є O S D C P T J K Pg N Perbandingan ukuran dengan rata-rata ukuran manusia Status konservasi Risiko Rendah (IUCN 3.1)[2] CITES Apendiks I (CITES)[3] Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Artiodactyla Infraordo: Cetacea Parvordo: Mysticeti Famili: Eschrichtiidae Genus: Eschrichtius Spesies: Eschrichtius robustusLilljeborg, 1861 Peta persebaran …

Lazzaretto di FiladelfiaFacciata del lazzaretto nel 2009LocalizzazioneStato Stati Uniti LocalitàFiladelfia Coordinate39°51′38″N 75°18′02″W / 39.860556°N 75.300556°W39.860556; -75.300556Coordinate: 39°51′38″N 75°18′02″W / 39.860556°N 75.300556°W39.860556; -75.300556 Informazioni generaliCondizioniIn uso Costruzionefine XVIII secolo StileStile Federale Usoisolamento pazienti contagiosi Modifica dati su Wikidata · Manuale Il Lazzar…
Pedro Cea Informasi pribadiNama lengkap José Pedro CeaTanggal lahir (1900-09-01)1 September 1900Tempat lahir Redondela, GaliciaTanggal meninggal 18 September 1970(1970-09-18) (umur 70)Tempat meninggal Montevideo, UruguayKarier senior*Tahun Tim Tampil (Gol) Nacional Tim nasional1923-1932 Uruguay 27 (13)Kepelatihan1941-1942 Uruguay Prestasi Mewakili Uruguay Sepak bola Pria 1924 Paris Kompetisi Tim 1928 Amsterdam Kompetisi Tim * Penampilan dan gol di klub senior hanya dihitung dari liga…

Members of the New South Wales Legislative Council who served in the 50th Parliament were affected by the 1991 referendum which reduced the number of members and reduced their term from three terms of the Legislative Assembly to two terms, meaning the maximum term was eight years. The Council consisted of 42 members, 12 elected in 1984, 15 elected in 1988 and 15 elected in 1991. Half of the council would face re-election in 1995 and half did not face re-election until 1999.[1][2]…

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �…

Chambérycomune Chambéry – VedutaPanorama della città LocalizzazioneStato Francia RegioneAlvernia-Rodano-Alpi Dipartimento Savoia ArrondissementChambéry CantoneChambéry-1Chambéry-2Chambéry-3 AmministrazioneSindacoThierry Repentin (PS) dal 4-7-2020 TerritorioCoordinate45°33′59″N 5°55′15″E / 45.566389°N 5.920833°E45.566389; 5.920833 (Chambéry)Coordinate: 45°33′59″N 5°55′15″E / 45.566389°N 5.920833°E45.566389; …

Thai dessert Sarim, served with ice on top Sarim (Thai: ซ่าหริ่ม, pronounced [sâːrìm]; or ซาหริ่ม, pronounced [sāːrìm]) is a Thai dessert. It consists of colourful (usually pink and green) thin noodles made from mung bean flour in coconut milk and syrup, served cold with crushed ice.[1] The dish is mentioned in the Kap He Chom Khrueang Khao Wan poem of King Rama II (r. 1809 – 1824), though back then it was seasoned with patchouli rath…
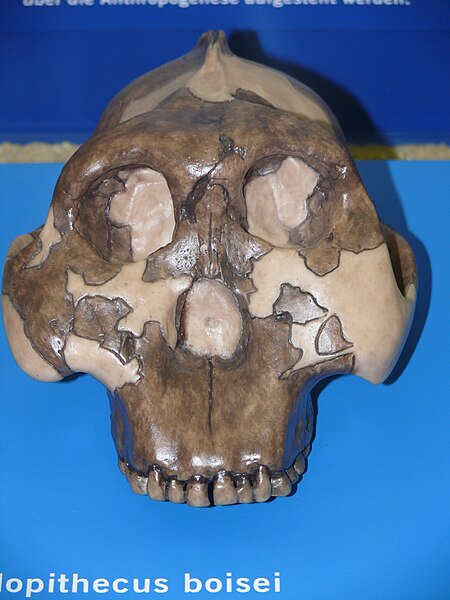
Paranthropus boiseiRentang fosil: Pliosen-Pleistosen Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Primates Famili: Hominidae Genus: Paranthropus Spesies: P. boisei Nama binomial Paranthropus boisei(Mary Leakey, 1959) Paranthropus boisei (awalnya disebut Zinjanthropus boisei dan lalu Australopithecus boisei) adalah hominin awal dan dideskripsikan sebagai spesies Paranthropus terbesar. Spesies ini hidup sekitar 2.6 hingga 1.2 juta tahun yang lalu selama Pliosen …

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1] �…

Chief Wilson of the Pittsburgh Pirates set the all-time record for triples in a season with 36 in 1912. In baseball, a triple is recorded when the ball is hit so that the batter is able to advance all the way to third base, scoring any runners who were already on base, with no errors by the defensive team on the play. In Major League Baseball (MLB), a player in each league [L] is recognized for leading the league in triples.[1] Only triples hit in a particular league count toward that le…

Saudi Arabian novelist (born 1979) Mohammed Hasan AlwanBorn(1979-08-27)27 August 1979Riyadh, Saudi ArabiaNationalitySaudi ArabianGenreNovels, short stories Mohammed Hasan Alwan (born 27 August 1979) is a Saudi Arabian novelist.[1] He was born in Riyadh and studied Computer Information Systems at King Saud University, obtaining a bachelor's degree in 2002. He also obtained an MBA from the University of Portland, Oregon in 2008 and Ph.D from Carleton University, Ottawa in 2016.[2] …

1940 film by Frank Lloyd The Howards of VirginiaNewspaper advertisementDirected byFrank LloydScreenplay bySidney BuchmanBased onThe Tree of Liberty 1939 novelby Elizabeth PageProduced byFrank LloydJack H. Skirball (associate producer)StarringCary GrantMartha ScottCedric HardwickeCinematographyBert GlennonEdited byPaul WeatherwaxMusic byRichard HagemanDistributed byColumbia PicturesRelease date September 19, 1940 (1940-09-19) Running time122 minutesCountryUnited StatesLanguageEngli…

此條目翻譯品質不佳。翻譯者可能不熟悉中文或原文語言,也可能使用了機器翻譯。請協助翻譯本條目或重新編寫,并注意避免翻译腔的问题。明顯拙劣的翻譯請改掛{{d|G13}}提交刪除。 「希拉克」重定向至此。關於法国洛泽尔省的同名市镇,請見「希拉克 (洛泽尔省)」。 雅克·勒内·希拉克Jacques René Chirac 第22任法國總統安道爾大公任期1995年5月17日—2007年5月16日总…

No debe confundirse con el Consejo Europeo, distinto y que reúne a los jefes de Estado y/o de gobierno de los 27 Estados de la Unión; o el Consejo de Europa, organización internacional (independiente y ajena a la UE) de cooperación de todos los países europeos. Consejo de la Unión EuropeaConsejo Edificio Europa, Bruselas (Bélgica)Información generalÁmbito Unión EuropeaTipo Cámara Alta(bicameral)LiderazgoPresidencia de turno (duración de 6 meses) Bélgica Bélgica1º semestre de …

Måneskin Måneskin en 2018. De gauche à droite : Ethan Torchio, Victoria De Angelis, Damiano David et Thomas RaggiInformations générales Pays d'origine Italie Genre musical Rock AlternatifGlam RockPop RockFunk Rock Années actives Depuis 2016 Labels RCASonyEpic Site officiel www.maneskin.it Composition du groupe Membres Damiano DavidVictoria De Angelis Thomas RaggiEthan Torchio Logo de Måneskin.modifier Måneskin (« Clair de Lune » en danois) est un groupe de rock italien, …