Weil group
|
Read other articles:

L'Assomption merupakan sebuah pinggiran kota lepas pulau Montreal, di baratlaut Quebec, Kanada, di Sungai L'Assomption. Merupakan kedudukan dari Kotamadya Kabupaten Regional L'Assomption. Terletak di luar wilayah urban Montreal. Sebagian ekonominya bergantung pada industri pertanian di daratan sekitarnya. Juga merupakan pusat budaya di daerah itu. Kota ini dikenal sebagai rumah bagi band metal Reanimator, dapat terdengar teriakan Merci L'Assomption! (yang berarti Terima kasih L'Assomption) di ak…

You can help expand this article with text translated from the corresponding article in Spanish. (May 2021) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this template: there are alread…

Bubuk kakao Padatan kakao adalah campuran dari berbagai senyawa setelah mentega kakao diekstraksi dari biji kakao. Umumnya dijual dalam bentuk bubuk kakao. Perbandingan antara padatan kakao dengan mentega kakao dalam biji kakao kurang lebih 50:50.[1] Dalam pembuatan coklat, padatan kakao dibutuhkan untuk menambah massa dan umumnya digunakan pada coklat berkualitas rendah. Sedangkah coklat kualitas tinggi menggunakan lebih banyak mentega kakao dibandingkan padatan kakao. Sifat fisik Padat…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari List of accolades received by Thani Oruvan di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai ba…
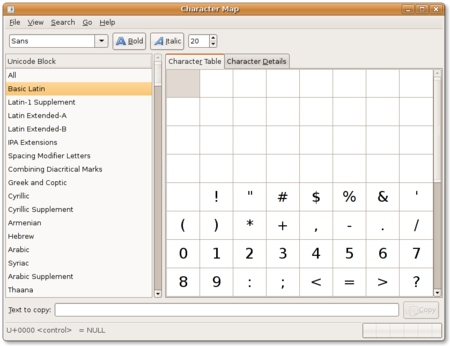
Representation of phonetic symbols in the Unicode Standard This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Phonetic symbols in Unicode – news · newspapers · books · scholar · JSTOR (January 2016) (Learn how and when to remove this template message) This article contains phonetic symbols. Without proper renderin…

Layar pada Pekan Olahraga Nasional 2021LokasiPantai Hamadi TNI AL, JayapuraTanggal3–12 Oktober 2021← 20162024 → Medali Perolehan medali * Tuan rumah penyelenggara (Papua)PeringkatProvinsiEmasPerakPerungguTotal1 Kalimantan Timur52292 Banten30253 Daerah Khusus Ibukota Jakarta25074 Kepulauan Riau23055 Jawa Timur21476 Papua*20247 Bali10018 Jawa Barat03479 Kalimantan Utara0101 Lampung0101 Papua…

مطار عثماني الدولي إياتا: ZYL – ايكاو: VGSY موجز يخدم سلهت البلد بنغلاديش الموقع إقليم سلهت الارتفاع 50 قدم إحداثيات 24°57′48″N 91°52′01″E / 24.963333333333°N 91.866944444444°E / 24.963333333333; 91.866944444444 الخريطة تعديل مصدري - تعديل مطار عثماني الدولي (بالبنغالية: ওসমা�…

Deputy Chief Ministers of BangsamoroIncumbentAli Solaiman (Deputy for the Mainland)Albakil Jikiri (Deputy for the Islands)NominatorChief MinisterAppointerBangsamoro ParliamentConstituting instrumentBangsamoro Organic LawInaugural holderAli Solaiman(Deputy for the Mainland)Abdul Sahrin(Deputy for the Islands)Formation2019; 5 years ago (2019)SuccessionFirst, the Deputy Chief Minister senior in age becomes acting Chief Minister in an event of a vacancy The deputy chief ministers o…

Sports radio station in San Diego KWFNSan Diego, CaliforniaUnited StatesBroadcast areaGreater San DiegoFrequency97.3 MHz (HD Radio)Branding97.3 The FanProgrammingLanguage(s)EnglishFormatSports radioSubchannelsHD2: The Angry Playlist (active rock)HD3: The Bet (sports gambling)Affiliations CBS Sports Radio Navy Midshipmen San Diego Padres Sports USA Radio Network Westwood One Sports OwnershipOwnerAudacy, Inc.(Audacy License, LLC, as Debtor-in-Possession)Sister stationsKBZTKSONKXSNKYXYHistoryFirst …

This is a list of astronauts, who are in a restricted sense, Asians. If Asian is restricted to refer to people from the continent of Asia, exclusive of Asian Russia and Turkey, who are not of predominantly European, African, or American ancestry, then the list is as follows: The first country listed is that of citizenship; the second, if any, is that of the Asian country of birth and/or ancestry, where different. Those of Asian ancestry but were born outside Asia are excluded. The table lists as…

Radio station in North Charleston, South CarolinaWXLYNorth Charleston, South CarolinaBroadcast areaCharleston metropolitan area, South Carolina LowcountryFrequency102.5 MHz (HD Radio)BrandingY102.5ProgrammingFormatAdult contemporarySubchannelsHD2: Radio by Grace (Christian radio)OwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsWEZL, WRFQ, WSCC-FMHistoryFirst air dateApril 1958 (66 years ago) (1958-04) as WCSC-FMFormer call signsWCSC-FM (1958-?)WKTM (?–1984)Te…

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Maribyrnong College – news · newspapers · books · scholar · JSTOR (June 2020) (Learn how and when to remove this message) Public sports high school in Maribyrnong, Melbourne, Victoria, AustraliaMaribyrnong CollegeMaribyrnong College entrance and elevated classroom…

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: WBDG – news · newspapers · books · scholar · JSTOR (March 2010) (Learn how and when to remove this message) Radio station in Indianapolis, IndianaWBDGIndianapolis, IndianaBroadcast areaIndianapolis areaFrequency90.9 MHz (HD Radio)BrandingGiant 90.9 FMProgrammingFo…

لمعانٍ أخرى، طالع جدة (توضيح). جدة مدينة جدة جدةشعار أمانة جدة اللقب عروس البحر الأحمر[1] تقسيم إداري البلد السعودية[2][3] عاصمة لـ محافظة جدة المنطقة منطقة مكة المكرمة المحافظة محافظة جدة المسؤولون أمير المنطقة خالد الفيصل بن عبد العزيز آل سعود نائب أمير …

Tour de Drenthe féminin 2011 GénéralitésCourse5e Tour de Drenthe fémininCompétitionCoupe du monde féminine de cyclisme sur route 2011 CDMDate16 avril 2011Distance132,8 kmPays Pays-BasLieu de départHoogeveenLieu d'arrivéeHoogeveenÉquipes26Partantes156Arrivantes123Vitesse moyenne39,202 km/hRésultatsVainqueur Marianne Vos (Nederland Bloeit)Deuxième Kirsten Wild (AA Drink-Leontien.nl)Troisième Giorgia Bronzini (Colavita Forno d'Asolo) ◀20102012▶Documentation La 5e éd…

His Excellency赫瓦贾·纳齐姆丁爵士খাজা নাজিমুদ্দীন خواجہ ناظِمُ الدّینCIE, KCIE摄于1948年第2任巴基斯坦總理任期1951年10月17日—1953年4月17日君主佐治六世伊莉沙白二世总督古拉姆·穆罕默德前任利雅卡特·阿里·汗继任Mohammad Ali Bogra(英语:Mohammad Ali Bogra)第2任巴基斯坦總督(英语:Governor-General of Pakistan)任期1948年9月14日—1951年10月17日君主�…

Exchange of mass, energy, and momentum between observed and studied systems For the textbook, see Transport Phenomena (book). Part of a series onChemical engineering Outline History Index Fundamentals Industry Engineer Process Unit operations Kinetics Transport phenomena Unit processes Chemical plant Chemical reactor Separation processes Aspects Heat transfer Mass transfer Fluid dynamics Process design Process control Chemical thermodynamics Reaction engineering Glossaries Glossary of chemistry …

LafuenteUbicaciónCoordenadas 34°37′18″S 58°22′01″O / -34.62166667, -58.36694444Dirección Avenida General Francisco Fernández de la Cruz y LafuenteSector Villa SoldatiComuna 8Localidad Buenos AiresDatos de la estaciónInauguración 14 de agosto de 2013 (10 años)Plataformas 2, (Separadas)Propietario Gobierno de la Ciudad de Buenos AiresOperador 23 76 101 143 150Líneas Varela ← → Mariano Acosta [movilidad.buenosaires.gob.ar/metrobus/ Sitio oficial][edita…

It has been suggested that 2024 Iran–Pakistan border skirmishes be merged into this article. (Discuss) Proposed since January 2024. Insurgency in Pakistan and Iran Insurgency in BalochistanPhysical map of Balochistan, Pakistan (detailed map of Pakistan conflicts)DateJuly 1948 – present[11] (75 years and 10 months) Main Phases: 1948-50 1958–60 1963–69 1973–77 2003–present LocationBalochistan, Iran–Pakistan border: Balochistan, Pakistan Sistan and Baluchestan, IranS…

Nama ini menggunakan cara penamaan Portugis. Nama keluarga pertama atau maternalnya adalah Regufe dan nama keluarga kedua atau paternalnya adalah Alves. Bruno Alves Alves bersama Portugal pada 2018Informasi pribadiNama lengkap Bruno Eduardo Regufe AlvesTanggal lahir 27 November 1981 (umur 42)Tempat lahir Póvoa de Varzim, PortugalTinggi 1,87 m (6 ft 1+1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini AEK Athens (Direktur Olahraga)Karier junior1992–1998 Varzim19…
