Diseño de Filtros de Respuesta Finita al Impulso
Este aviso fue puesto el 18 de mayo de 2010.
Diseño de filtros de Respuesta Finita al Impulso (del inglés : FIR
s muestras N+1 en la duración.
El filtro FIR básico se caracteriza por Ec. 1
y
(
n
)
=
∑
k
=
0
N
−
1
h
(
k
)
x
(
n
−
k
)
{\displaystyle \scriptstyle y(n)=\sum _{k=0}^{N-1}h(k)x(n-k)}
Ec. 2
H
(
z
)
=
∑
k
=
0
N
−
1
h
(
k
)
z
−
k
{\displaystyle \scriptstyle \mathrm {H} (z)=\sum _{k=0}^{N-1}h(k)z^{-k}}
h
(
k
)
{\displaystyle h(k)}
k
=
0
,
1
,
.
.
.
,
N
−
2
,
N
−
1
{\displaystyle \scriptstyle k={0,\ 1,\ ...,\ N-2,\ N-1}}
H
(
z
)
{\displaystyle \mathrm {H} (z)}
N
{\displaystyle N}
Ec. 1 es la ecuación en diferencias para filtros FIR. Es una ecuación en el dominio del tiempo y describe al filtro FIR en la forma no recursiva, la muestra de salida actual,
y
(
n
)
{\displaystyle y(n)}
x
(
n
)
{\displaystyle x(n)}
Ec. 1 son siempre estables. Ec. 2 es la función de transferencia del filtro. Provee un medio para analizar el filtro, por ejemplo evaluar la respuesta en frecuencia.
Los filtros FIR pueden tener una respuesta exactamente de fase lineal.
Los filtros FIR son muy fáciles de implementar, Todos los Procesadores DSP disponibles tienen arquitecturas que son apropiados para el filtrado FIR. Los filtros FIR no recursivos sufren menos los efectos de longitud de palabra que los filtros IIR. Los filtros FIR recursivos también existen y pueden ofrecer ventajas informáticas significativas.
Considérese:
x
(
n
)
=
{
4.5
,
5.4
,
6.3
,
7.2
,
8.1
,
9.0
}
{\displaystyle \scriptstyle x(n)=\lbrace 4.5,\ 5.4,\ 6.3,\ 7.2,\ 8.1,\ 9.0\rbrace }
M
{\displaystyle M}
x
(
n
)
{\displaystyle x(n)}
→
M
=
6
{\displaystyle \scriptstyle \rightarrow \ M=6}
h
(
n
)
=
{
0.9
,
1.8
,
2.7
,
3.6
}
{\displaystyle \scriptstyle h(n)=\lbrace 0.9,\ 1.8,\ 2.7,\ 3.6\rbrace }
N
{\displaystyle N}
h
(
n
)
{\displaystyle h(n)}
→
N
=
4
{\displaystyle \scriptstyle \rightarrow \ N=4}
y
(
n
)
{\displaystyle y(n)}
y
(
n
)
=
∑
k
=
0
N
−
1
h
(
k
)
x
(
n
−
k
)
{\displaystyle \scriptstyle y(n)=\sum _{k=0}^{N-1}h(k)x(n-k)}
y
(
n
)
=
∑
k
=
0
M
−
1
x
(
k
)
h
(
n
−
k
)
{\displaystyle \scriptstyle y(n)=\sum _{k=0}^{M-1}x(k)h(n-k)}
y
(
n
)
=
∑
k
=
0
3
h
(
k
)
x
(
n
−
k
)
{\displaystyle \scriptstyle y(n)=\sum _{k=0}^{3}h(k)x(n-k)}
y
(
0
)
=
x
(
0
)
∗
h
(
0
)
=
h
(
0
)
x
(
0
)
+
h
(
1
)
x
(
−
1
)
+
h
(
2
)
x
(
−
2
)
+
h
(
3
)
x
(
−
3
)
{\displaystyle \scriptstyle y(0)=x(0)*h(0)=h(0)x(0)+h(1)x(-1)+h(2)x(-2)+h(3)x(-3)}
y
(
0
)
=
0.9
×
4.5
+
1.8
×
0
+
2.7
×
0
+
3.6
×
0
=
4.05
{\displaystyle \scriptstyle y(0)=0.9\times 4.5+1.8\times 0+2.7\times 0+3.6\times 0=4.05}
y
(
1
)
=
x
(
1
)
∗
h
(
1
)
=
h
(
0
)
x
(
1
)
+
h
(
1
)
x
(
0
)
+
h
(
2
)
x
(
−
1
)
+
h
(
3
)
x
(
−
2
)
{\displaystyle \scriptstyle y(1)=x(1)*h(1)=h(0)x(1)+h(1)x(0)+h(2)x(-1)+h(3)x(-2)}
y
(
1
)
=
0.9
×
5.4
+
1.8
×
4.5
+
2.7
×
0
+
3.6
×
0
=
12.96
{\displaystyle \scriptstyle y(1)=0.9\times 5.4+1.8\times 4.5+2.7\times 0+3.6\times 0=12.96}
y
(
2
)
=
x
(
2
)
∗
h
(
2
)
=
h
(
0
)
x
(
2
)
+
h
(
1
)
x
(
1
)
+
h
(
2
)
x
(
0
)
+
h
(
3
)
x
(
−
1
)
{\displaystyle \scriptstyle y(2)=x(2)*h(2)=h(0)x(2)+h(1)x(1)+h(2)x(0)+h(3)x(-1)}
y
(
2
)
=
0.9
×
6.3
+
1.8
×
5.4
+
2.7
×
4.5
+
3.6
×
0
=
27.54
{\displaystyle \scriptstyle y(2)=0.9\times 6.3+1.8\times 5.4+2.7\times 4.5+3.6\times 0=27.54}
y
(
3
)
=
x
(
3
)
∗
h
(
3
)
=
h
(
0
)
x
(
3
)
+
h
(
1
)
x
(
2
)
+
h
(
2
)
x
(
1
)
+
h
(
3
)
x
(
0
)
{\displaystyle \scriptstyle y(3)=x(3)*h(3)=h(0)x(3)+h(1)x(2)+h(2)x(1)+h(3)x(0)}
y
(
3
)
=
0.9
×
7.2
+
1.8
×
6.3
+
2.7
×
5.4
+
3.6
×
4.5
=
48.6
{\displaystyle \scriptstyle y(3)=0.9\times 7.2+1.8\times 6.3+2.7\times 5.4+3.6\times 4.5=48.6}
y
(
4
)
=
x
(
4
)
∗
h
(
4
)
=
h
(
0
)
x
(
4
)
+
h
(
1
)
x
(
3
)
+
h
(
2
)
x
(
2
)
+
h
(
3
)
x
(
1
)
{\displaystyle \scriptstyle y(4)=x(4)*h(4)=h(0)x(4)+h(1)x(3)+h(2)x(2)+h(3)x(1)}
y
(
2
)
=
0.9
×
8.1
+
1.8
×
7.2
+
2.7
×
6.3
+
3.6
×
5.4
=
56
,
7
{\displaystyle \scriptstyle y(2)=0.9\times 8.1+1.8\times 7.2+2.7\times 6.3+3.6\times 5.4=56,7}
y
(
5
)
=
x
(
5
)
∗
h
(
5
)
=
h
(
0
)
x
(
5
)
+
h
(
1
)
x
(
4
)
+
h
(
2
)
x
(
3
)
+
h
(
3
)
x
(
2
)
{\displaystyle \scriptstyle y(5)=x(5)*h(5)=h(0)x(5)+h(1)x(4)+h(2)x(3)+h(3)x(2)}
y
(
5
)
=
0.9
×
9.0
+
1.8
×
8.1
+
2.7
×
7.2
+
3.6
×
6.3
=
64.8
{\displaystyle \scriptstyle y(5)=0.9\times 9.0+1.8\times 8.1+2.7\times 7.2+3.6\times 6.3=64.8}
y
(
n
)
=
{
4.05
,
12.96
,
27.54
,
48.6
,
56.7
,
64.8
}
{\displaystyle \scriptstyle y(n)=\lbrace 4.05,\ 12.96,\ 27.54,\ 48.6,\ 56.7,\ 64.8\rbrace }
calculando en la otra forma:
y
(
n
)
=
∑
k
=
0
5
x
(
k
)
h
(
n
−
k
)
{\displaystyle \scriptstyle y(n)=\sum _{k=0}^{5}x(k)h(n-k)}
y
(
0
)
=
x
(
0
)
∗
h
(
0
)
=
x
(
0
)
h
(
0
)
+
x
(
1
)
h
(
−
1
)
+
x
(
2
)
h
(
−
2
)
+
x
(
3
)
h
(
−
3
)
+
x
(
4
)
h
(
−
4
)
+
x
(
5
)
h
(
−
5
)
{\displaystyle \scriptstyle y(0)=x(0)*h(0)=x(0)h(0)+x(1)h(-1)+x(2)h(-2)+x(3)h(-3)+x(4)h(-4)+x(5)h(-5)}
y
(
0
)
=
4.5
×
0.9
+
5.4
×
0
+
6.3
×
0
+
7.2
×
0
+
8.1
×
0
+
9.0
×
0
=
4.05
{\displaystyle \scriptstyle y(0)=4.5\times 0.9+5.4\times 0+6.3\times 0+7.2\times 0+8.1\times 0+9.0\times 0=4.05}
y
(
1
)
=
x
(
1
)
∗
h
(
1
)
=
x
(
0
)
h
(
1
)
+
x
(
1
)
h
(
0
)
+
x
(
2
)
h
(
−
1
)
+
x
(
3
)
h
(
−
2
)
+
x
(
4
)
h
(
−
3
)
+
x
(
5
)
h
(
−
4
)
{\displaystyle \scriptstyle y(1)=x(1)*h(1)=x(0)h(1)+x(1)h(0)+x(2)h(-1)+x(3)h(-2)+x(4)h(-3)+x(5)h(-4)}
y
(
1
)
=
4.5
×
1.8
+
5.4
×
0.9
+
6.3
×
0
+
7.2
×
0
+
8.1
×
0
+
9.0
×
0
=
12.96
{\displaystyle \scriptstyle y(1)=4.5\times 1.8+5.4\times 0.9+6.3\times 0+7.2\times 0+8.1\times 0+9.0\times 0=12.96}
y
(
2
)
=
x
(
2
)
∗
h
(
2
)
=
x
(
0
)
h
(
2
)
+
x
(
1
)
h
(
1
)
+
x
(
2
)
h
(
0
)
+
x
(
3
)
h
(
−
1
)
+
x
(
4
)
h
(
−
2
)
+
x
(
5
)
h
(
−
3
)
{\displaystyle \scriptstyle y(2)=x(2)*h(2)=x(0)h(2)+x(1)h(1)+x(2)h(0)+x(3)h(-1)+x(4)h(-2)+x(5)h(-3)}
y
(
2
)
=
4.5
×
2.7
+
5.4
×
1.8
+
6.3
×
0.9
+
7.2
×
0
+
8.1
×
0
+
9.0
×
0
=
27.54
{\displaystyle \scriptstyle y(2)=4.5\times 2.7+5.4\times 1.8+6.3\times 0.9+7.2\times 0+8.1\times 0+9.0\times 0=27.54}
y
(
3
)
=
x
(
3
)
∗
h
(
3
)
=
x
[
0
]
h
(
3
)
+
x
(
1
)
h
(
2
)
+
x
(
2
)
h
(
1
)
+
x
(
3
)
h
(
0
)
+
x
(
4
)
h
(
−
1
)
+
x
(
5
)
h
(
−
2
)
{\displaystyle \scriptstyle y(3)=x(3)*h(3)=x[0]h(3)+x(1)h(2)+x(2)h(1)+x(3)h(0)+x(4)h(-1)+x(5)h(-2)}
y
(
3
)
=
4.5
×
3.6
+
5.4
×
2.7
+
6.3
×
1.8
+
7.2
×
0.9
+
8.1
×
0
+
9.0
×
0
=
48.6
{\displaystyle \scriptstyle y(3)=4.5\times 3.6+5.4\times 2.7+6.3\times 1.8+7.2\times 0.9+8.1\times 0+9.0\times 0=48.6}
y
(
4
)
=
x
(
4
)
∗
h
(
4
)
=
x
(
0
)
h
(
4
)
+
x
(
1
)
h
(
3
)
+
x
(
2
)
h
(
2
)
+
x
(
3
)
h
(
1
)
+
x
(
4
)
h
(
0
)
+
x
(
5
)
h
(
−
1
)
{\displaystyle \scriptstyle y(4)=x(4)*h(4)=x(0)h(4)+x(1)h(3)+x(2)h(2)+x(3)h(1)+x(4)h(0)+x(5)h(-1)}
y
(
4
)
=
4.5
×
0
+
5.4
×
3.6
+
6.3
×
2.7
+
7.2
×
1.8
+
8.1
×
0.9
+
9.0
×
0
=
56.7
{\displaystyle \scriptstyle y(4)=4.5\times 0+5.4\times 3.6+6.3\times 2.7+7.2\times 1.8+8.1\times 0.9+9.0\times 0=56.7}
y
(
5
)
=
x
(
5
)
∗
h
(
5
)
=
x
(
0
)
h
(
5
)
+
x
(
1
)
h
(
4
)
+
x
(
2
)
h
(
3
)
+
x
(
3
)
h
(
2
)
+
x
(
4
)
h
(
1
)
+
x
(
5
)
h
(
0
)
{\displaystyle \scriptstyle y(5)=x(5)*h(5)=x(0)h(5)+x(1)h(4)+x(2)h(3)+x(3)h(2)+x(4)h(1)+x(5)h(0)}
y
(
5
)
=
4.5
×
0
+
5.4
×
0
+
6.3
×
3.6
+
7.2
×
2.7
+
8.1
×
1.8
+
9.0
×
0.9
=
64.8
{\displaystyle \scriptstyle y(5)=4.5\times 0+5.4\times 0+6.3\times 3.6+7.2\times 2.7+8.1\times 1.8+9.0\times 0.9=64.8}
y
(
n
)
=
{
4.05
,
12.96
,
27.54
,
48.6
,
56.7
,
64.8
}
{\displaystyle \scriptstyle y(n)=\lbrace 4.05,\ 12.96,\ 27.54,\ 48.6,\ 56.7,\ 64.8\rbrace }
Hay exactamente cuatro tipos de filtros FIR de fase lineal, dependiendo de si
N
{\displaystyle N}
h
(
n
)
{\displaystyle h(n)}
Resumen de los puntos claves de los cuatro tipos de filtros FIR de fase lineal
ω
=
2
π
f
{\displaystyle \omega =2\pi f}
a
(
0
)
=
h
[
(
N
−
1
)
/
2
]
{\displaystyle a(0)=h[(N-1)/2]}
a
(
n
)
=
2
h
[
(
N
−
1
)
/
2
−
n
]
{\displaystyle a(n)=2h[(N-1)/2-n]}
b
(
n
)
=
2
h
[
N
/
2
−
n
]
{\displaystyle b(n)=2h[N/2-n]}
La respuesta en frecuencia de un filtro tipo 2 (simetría positiva y tamaño par) es siempre cero en
f
=
0.5
{\displaystyle f=0.5}
90
∘
{\displaystyle \scriptstyle 90^{\circ }}
f
=
0
{\displaystyle f=0}
f
=
0.5
{\displaystyle f=0.5}
90
∘
{\displaystyle \scriptstyle 90^{\circ }}
Se usa el hecho de que la respuesta en frecuencia de un filtro
H
D
(
ω
)
{\displaystyle H_{D}(\omega )}
h
D
(
n
)
{\displaystyle h_{D}(n)}
h
D
(
n
)
=
(
1
/
2
π
)
∫
−
π
π
H
D
(
ω
)
e
j
ω
n
d
ω
{\displaystyle h_{D}(n)=(1/2\pi )\int _{-\pi }^{\pi }H_{D}(\omega )e^{j\omega n}\,d\omega }
El subíndice
D
{\displaystyle _{D}}
Diferentes respuestas al impulso ideales
h
D
(
n
)
{\displaystyle h_{D}(n)}
Tipo de filtro
h
D
(
n
)
{\displaystyle h_{D}(n)}
n
≠
0
{\displaystyle n\neq 0}
h
D
(
0
)
{\displaystyle h_{D}(0)}
Pasa bajo
2
f
c
sin
(
n
ω
c
)
n
ω
c
{\displaystyle \scriptstyle 2f_{c}\textstyle {\frac {\sin(n\omega _{c})}{n\omega _{c}}}}
2
f
c
{\displaystyle 2f_{c}}
Pasa alto
−
2
f
c
sin
(
n
ω
c
)
n
ω
c
{\displaystyle \scriptstyle -2f_{c}\textstyle {\frac {\sin(n\omega _{c})}{n\omega _{c}}}}
1
−
2
f
c
{\displaystyle 1-2f_{c}}
Pasa banda
2
f
a
sin
(
n
ω
a
)
n
ω
a
−
2
f
b
sin
(
n
ω
b
)
n
ω
b
{\displaystyle \scriptstyle 2f_{a}\textstyle {\frac {\sin(n\omega _{a})}{n\omega _{a}}}\scriptstyle -2f_{b}\textstyle {\frac {\sin(n\omega _{b})}{n\omega _{b}}}}
2
(
f
a
−
f
b
)
{\displaystyle 2(f_{a}-f_{b})}
Para banda
2
f
b
sin
(
n
ω
b
)
n
ω
b
−
2
f
a
sin
(
n
ω
a
)
n
ω
a
{\displaystyle \scriptstyle 2f_{b}{\frac {\sin(n\omega _{b})}{n\omega _{b}}}\scriptstyle -2f_{a}\textstyle {\frac {\sin(n\omega _{a})}{n\omega _{a}}}}
1
−
2
(
f
a
−
f
b
)
{\displaystyle 1-2(f_{a}-f_{b})}
N
{\displaystyle N}
f
c
{\displaystyle f_{c}}
f
b
{\displaystyle f_{b}}
f
a
{\displaystyle f_{a}}
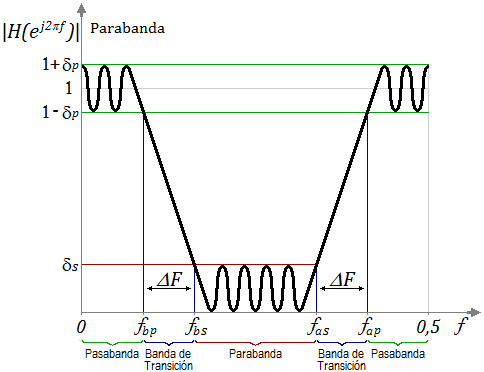
Especificaciones de filtros FIR
Especificación de respuesta Magnitud Frecuencia para diferentes tipos de filtro.
h
(
n
)
{\displaystyle h(n)}
h
d
(
n
)
{\displaystyle h_{d}(n)}
ventana
w
(
n
)
{\displaystyle w(n)}
h
(
n
)
=
h
d
(
n
)
w
(
n
)
{\displaystyle h(n)=h_{d}(n)w(n)}
Kaiser
Nombre
Ancho de Transición
Rizo (dB)
Relación (dB)
Atenuación (dB)
función ventana
w
(
n
)
{\displaystyle w(n)}
|
n
|
≤
(
N
−
1
)
/
2
{\displaystyle \textstyle |n|\scriptstyle \leq \left(N-1\right)/2}
Rectangular
0.9
/
N
{\displaystyle 0.9/N}
0.7416
13
21
1
Hanning
3.1
/
N
{\displaystyle 3.1/N}
0.0546
31
44
0.5
+
0.5
c
o
s
(
2
π
n
N
)
{\displaystyle \scriptstyle 0.5+0.5\textstyle cos\scriptstyle \left({\frac {2\textstyle \pi n}{N}}\right)}
Hamming
3.3
/
N
{\displaystyle 3.3/N}
0.0194
41
53
0.54
−
0.46
c
o
s
(
2
π
n
N
)
{\displaystyle \scriptstyle 0.54-0.46\textstyle cos\scriptstyle \left({\frac {2\textstyle \pi n}{N}}\right)}
Blackman
5.5
/
N
{\displaystyle 5.5/N}
0.0017
57
75
0.42
−
0.50
c
o
s
(
2
π
n
N
−
1
)
+
0.08
c
o
s
(
4
π
n
N
−
1
)
{\displaystyle \scriptstyle 0.42-0.50\textstyle cos\scriptstyle \left({\frac {2\textstyle \pi n}{N\scriptstyle -1}}\right)+0.08\textstyle cos\scriptstyle \left({\frac {4\textstyle \pi n}{N\scriptstyle -1}}\right)}
Kaiser
5.71
/
N
(
β
=
8.96
)
{\displaystyle 5.71/N(\beta =8.96)}
0.000275
90
I
o
[
β
(
1
−
(
2
n
(
N
−
1
)
)
2
)
]
I
o
(
β
)
{\displaystyle \scriptstyle {\frac {I_{o}\left[\beta {\sqrt {\left(1-\left({\frac {2n}{\left(N-1\right)}}\right)^{2}\right)}}\right]}{I_{o}\left(\beta \right)}}}
De las funciones ventanas dispuestas en la tabla, se puede notar que:
La ventana de Blackman tiene una fuerte atenuación en parabanda, pero para alcanzarla necesita una banda de transición mayor.
La ventana de Hanning presenta una banda de transición menor, pero de igual forma su atenuación en la parabanda es menor.
La ventana de Hamming es la más usada porque se puede obtener una atenuación considerable con una banda de transición estrecha.
A manera de ejemplo se calcularán los coeficientes para los cuatro filtros con los siguientes parámetros:PasaBajo con Frecuencia de Corte 4000HzPasaAlto con Frecuencia de Corte 20000HzPasaBanda con Frecuencia Baja = 10000Hz, Frecuencia Alta = 14000HzParaBanda con Frecuencia Baja = 2000Hz, Frecuencia Alta = 22000HzN = 9Hamming
Δ
F
=
3
,
3
/
N
=
3
,
3
/
9
=
0
,
3667
{\displaystyle \Delta F=3,3/N=3,3/9=0,3667}
Así la Banda de Transición en Hz será:
B
a
n
d
a
T
r
a
n
s
i
c
i
o
n
=
Δ
F
×
F
r
e
c
u
e
n
c
i
a
M
u
e
s
t
r
e
o
=
0
,
3667
×
48000
H
z
=
17600
H
z
{\displaystyle \scriptstyle BandaTransicion=\Delta F\times FrecuenciaMuestreo=0,3667\times 48000Hz=17600Hz}
Para diferenciar la respuesta al impulso
h
(
n
)
{\displaystyle h(n)}
h
(
n
)
L
P
{\displaystyle h(n)_{LP}}
h
(
n
)
H
P
{\displaystyle h(n)_{HP}}
h
(
n
)
P
B
{\displaystyle h(n)_{PB}}
h
(
n
)
S
B
{\displaystyle h(n)_{SB}}
Los coeficientes para la ventana de Hamming serán:
n
{\displaystyle n}
w
(
n
)
=
0.54
+
0.46
×
c
o
s
(
2
π
n
N
)
{\displaystyle \scriptstyle w(n)=0.54+0.46\times \textstyle cos\scriptstyle \left({\frac {2\textstyle \pi n}{N}}\right)}
-4
w
(
−
4
)
=
0.54
+
0.46
×
c
o
s
(
2
×
π
×
−
4
9
)
=
0
,
9723
{\displaystyle \scriptstyle w(-4)=0.54+0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times -4}{9}}\textstyle \right)=0,9723}
-3
w
(
−
3
)
=
0.54
+
0.46
×
c
o
s
(
2
×
π
×
−
3
9
)
=
0
,
7700
{\displaystyle \scriptstyle w(-3)=0.54+0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times -3}{9}}\textstyle \right)=0,7700}
-2
w
(
−
2
)
=
0.54
−
0.46
×
c
o
s
(
2
×
π
×
−
2
9
)
=
0
,
4601
{\displaystyle \scriptstyle w(-2)=0.54-0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times -2}{9}}\textstyle \right)=0,4601}
-1
w
(
−
1
)
=
0.54
−
0.46
×
c
o
s
(
2
×
π
×
−
1
9
)
=
0
,
1876
{\displaystyle \scriptstyle w(-1)=0.54-0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times -1}{9}}\textstyle \right)=0,1876}
0
w
(
0
)
=
0.54
+
0.46
×
c
o
s
(
2
×
π
×
0
9
)
=
1
{\displaystyle \scriptstyle w(0)=0.54+0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times 0}{9}}\textstyle \right)=1}
1
w
(
1
)
=
0.54
−
0.46
×
c
o
s
(
2
×
π
×
1
9
)
=
0
,
1876
{\displaystyle \scriptstyle w(1)=0.54-0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times 1}{9}}\textstyle \right)=0,1876}
2
w
(
2
)
=
0.54
−
0.46
×
c
o
s
(
2
×
π
×
2
9
)
=
0
,
4601
{\displaystyle \scriptstyle w(2)=0.54-0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times 2}{9}}\textstyle \right)=0,4601}
3
w
(
3
)
=
0.54
−
0.46
×
c
o
s
(
2
×
π
×
3
9
)
=
0
,
7700
{\displaystyle \scriptstyle w(3)=0.54-0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times 3}{9}}\textstyle \right)=0,7700}
4
w
(
4
)
=
0.54
−
0.46
×
c
o
s
(
2
×
π
×
4
9
)
=
0
,
9723
{\displaystyle \scriptstyle w(4)=0.54-0.46\times \textstyle cos\scriptstyle \left({\frac {2\times \textstyle \pi \scriptstyle \times 4}{9}}\textstyle \right)=0,9723}
Filtro PasaBajo
f
c
=
f
p
+
Δ
F
/
2
=
4000
H
z
/
48000
H
z
+
0
,
3667
/
2
=
0
,
2667
{\displaystyle f_{c}=f_{p}+\Delta F/2=4000Hz/48000Hz+0,3667/2=0,2667}
ω
c
=
2
π
f
c
=
1
,
6755
{\displaystyle \omega _{c}=2\pi f_{c}=1,6755}
Recuerdese que para efectos de identificación:
h
(
n
)
→
h
(
n
)
L
P
{\displaystyle \scriptstyle h(n)\;\rightarrow \;h(n)_{LP}}
h
d
(
n
)
→
h
d
(
n
)
L
P
{\displaystyle \scriptstyle h_{d}(n)\;\rightarrow \;h_{d}(n)_{LP}}
n
{\displaystyle n}
h
d
(
n
)
L
P
=
2
f
c
sin
(
n
×
ω
c
)
n
ω
c
=
sin
(
n
×
ω
c
)
n
π
{\displaystyle \scriptstyle h_{d}(n)_{LP}=2\textstyle f_{c}{\frac {\sin \scriptstyle \left(n\times \omega _{c}\right)}{n\omega _{c}}}=\textstyle {\frac {\sin \left(n\times \omega _{c}\right)}{n\pi }}}
h
(
n
)
L
P
=
w
(
n
)
×
h
d
(
n
)
L
P
{\displaystyle \scriptstyle h(n)_{LP}=w(n)\times h_{d}(n)_{LP}}
-4
h
d
(
−
4
)
L
P
=
sin
(
−
4
×
1
,
6755
)
−
4
π
=
0
,
0324
{\displaystyle \scriptstyle h_{d}(-4)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle -4\times 1,6755\right)}{\scriptstyle -4\textstyle \pi }}\scriptstyle =0,0324}
h
(
−
4
)
L
P
=
w
(
−
4
)
×
h
d
(
−
4
)
L
P
=
0
,
1077
×
0
,
0324
=
0
,
0035
{\displaystyle \scriptstyle h(-4)_{LP}=w(-4)\times h_{d}(-4)_{LP}=0,1077\times 0,0324=0,0035}
-3
h
d
(
−
3
)
L
P
=
sin
(
−
3
×
1
,
6755
)
−
3
π
=
−
0
,
1009
{\displaystyle \scriptstyle h_{d}(-3)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle -3\times 1,6755\right)}{\scriptstyle -3\textstyle \pi }}\scriptstyle =-0,1009}
h
(
−
3
)
L
P
=
w
(
−
3
)
×
h
d
(
−
3
)
L
P
=
0
,
3100
×
−
0
,
1009
=
−
0
,
0313
{\displaystyle \scriptstyle h(-3)_{LP}=w(-3)\times h_{d}(-3)_{LP}=0,3100\times -0,1009=-0,0313}
-2
h
d
(
−
2
)
L
P
=
sin
(
−
2
×
1
,
6755
)
−
2
π
=
−
0
,
0331
{\displaystyle \scriptstyle h_{d}(-2)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle -2\times 1,6755\right)}{\scriptstyle -2\textstyle \pi }}\scriptstyle =-0,0331}
h
(
−
2
)
L
P
=
w
(
−
2
)
×
h
d
(
−
2
)
L
P
=
0
,
6199
×
−
0
,
0331
=
−
0
,
0205
{\displaystyle \scriptstyle h(-2)_{LP}=w(-2)\times h_{d}(-2)_{LP}=0,6199\times -0,0331=-0,0205}
-1
h
d
(
−
1
)
L
P
=
sin
(
−
1
×
1
,
6755
)
−
1
π
=
0
,
3166
{\displaystyle \scriptstyle h_{d}(-1)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle -1\times 1,6755\right)}{\scriptstyle -1\textstyle \pi }}\scriptstyle =0,3166}
h
(
−
1
)
L
P
=
w
(
−
2
)
×
h
d
(
−
1
)
L
P
=
0
,
8924
×
0
,
3166
=
0
,
2825
{\displaystyle \scriptstyle h(-1)_{LP}=w(-2)\times h_{d}(-1)_{LP}=0,8924\times 0,3166=0,2825}
0
h
d
(
0
)
L
P
=
2
×
f
c
=
2
×
0
,
2667
=
0
,
5334
{\displaystyle \scriptstyle h_{d}(0)_{LP}=2\times f_{c}=2\times 0,2667=0,5334}
h
(
0
)
L
P
=
w
(
0
)
×
h
d
(
0
)
L
P
=
1
,
0000
×
0
,
5334
=
0
,
5334
{\displaystyle \scriptstyle h(0)_{LP}=w(0)\times h_{d}(0)_{LP}=1,0000\times 0,5334=0,5334}
1
h
d
(
1
)
L
P
=
sin
(
1
×
1
,
6755
)
1
π
=
0
,
3166
{\displaystyle \scriptstyle h_{d}(1)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle 1\times 1,6755\right)}{\scriptstyle 1\textstyle \pi }}\scriptstyle =0,3166}
h
(
1
)
L
P
=
w
(
1
)
×
h
d
(
1
)
L
P
=
0
,
8924
×
0
,
3166
=
0
,
2825
{\displaystyle \scriptstyle h(1)_{LP}=w(1)\times h_{d}(1)_{LP}=0,8924\times 0,3166=0,2825}
2
h
d
(
2
)
L
P
=
sin
(
2
×
1
,
6755
)
2
π
=
−
0
,
0331
{\displaystyle \scriptstyle h_{d}(2)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle 2\times 1,6755\right)}{\scriptstyle 2\textstyle \pi }}\scriptstyle =-0,0331}
h
(
2
)
L
P
=
w
(
2
)
×
h
d
(
2
)
L
P
=
0
,
6199
×
−
0
,
0331
=
−
0
,
0205
{\displaystyle \scriptstyle h(2)_{LP}=w(2)\times h_{d}(2)_{LP}=0,6199\times -0,0331=-0,0205}
3
h
d
(
3
)
L
P
=
sin
(
3
×
1
,
6755
)
3
π
=
−
0
,
1009
{\displaystyle \scriptstyle h_{d}(3)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle 3\times 1,6755\right)}{\scriptstyle 3\textstyle \pi }}\scriptstyle =-0,1009}
h
(
3
)
L
P
=
w
(
3
)
×
h
d
(
3
)
L
P
=
0
,
3100
×
−
0
,
1009
=
−
0
,
0313
{\displaystyle \scriptstyle h(3)_{LP}=w(3)\times h_{d}(3)_{LP}=0,3100\times -0,1009=-0,0313}
4
h
d
(
4
)
L
P
=
sin
(
4
×
1
,
6755
)
4
π
=
0
,
0324
{\displaystyle \scriptstyle h_{d}(4)_{LP}=\textstyle {\frac {\sin \left(\scriptstyle 4\times 1,6755\right)}{\scriptstyle 4\textstyle \pi }}\scriptstyle =0,0324}
h
(
4
)
L
P
=
w
(
4
)
×
h
d
(
4
)
L
P
=
0
,
1077
×
0
,
0324
=
0
,
0035
{\displaystyle \scriptstyle h(4)_{LP}=w(4)\times h_{d}(4)_{LP}=0,1077\times 0,0324=0,0035}
Filtro PasaAlto
f
c
=
f
p
−
Δ
F
/
2
=
20000
H
z
/
48000
H
z
−
0
,
3667
/
2
=
0
,
2333
{\displaystyle f_{c}=f_{p}-\Delta F/2=20000Hz/48000Hz-0,3667/2=0,2333}
ω
c
=
2
π
f
c
=
1
,
4661
{\displaystyle \omega _{c}=2\pi f_{c}=1,4661}
Recuerdese que para efectos de identificación:
h
(
n
)
→
h
(
n
)
H
P
{\displaystyle \scriptstyle h(n)\;\rightarrow \;h(n)_{HP}}
h
d
(
n
)
→
h
d
(
n
)
H
P
{\displaystyle \scriptstyle h_{d}(n)\;\rightarrow \;h_{d}(n)_{HP}}
n
{\displaystyle n}
h
d
(
n
)
H
P
=
−
2
f
c
sin
(
n
×
ω
c
)
n
ω
c
=
−
sin
(
n
×
ω
c
)
n
π
{\displaystyle \scriptstyle h_{d}(n)_{HP}=-2\textstyle f_{c}{\frac {\sin \scriptstyle \left(n\times \omega _{c}\right)}{n\omega _{c}}}=\scriptstyle -\textstyle {\frac {\sin \left(n\times \omega _{c}\right)}{n\pi }}}
h
(
n
)
H
P
=
w
(
n
)
×
h
d
(
n
)
H
P
{\displaystyle \scriptstyle h(n)_{HP}=w(n)\times h_{d}(n)_{HP}}
-4
h
d
(
−
4
)
H
P
=
−
sin
(
−
4
×
1
,
4661
)
−
4
π
=
0
,
0324
{\displaystyle \scriptstyle h_{d}(-4)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle -4\times 1,4661\right)}{\scriptstyle -4\textstyle \pi }}\scriptstyle =0,0324}
h
(
−
4
)
H
P
=
w
(
−
4
)
×
h
d
(
−
4
)
H
P
=
0
,
1077
×
0
,
0324
=
0
,
0035
{\displaystyle \scriptstyle h(-4)_{HP}=w(-4)\times h_{d}(-4)_{HP}=0,1077\times 0,0324=0,0035}
-3
h
d
(
−
3
)
H
P
=
−
sin
(
−
3
×
1
,
4661
)
−
3
π
=
0
,
1009
{\displaystyle \scriptstyle h_{d}(-3)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle -3\times 1,4661\right)}{\scriptstyle -3\textstyle \pi }}\scriptstyle =0,1009}
h
(
−
3
)
H
P
=
w
(
−
3
)
×
h
d
(
−
3
)
H
P
=
0
,
3100
×
0
,
1009
=
0
,
0313
{\displaystyle \scriptstyle h(-3)_{HP}=w(-3)\times h_{d}(-3)_{HP}=0,3100\times 0,1009=0,0313}
-2
h
d
(
−
2
)
H
P
=
−
sin
(
−
2
×
1
,
4661
)
−
2
π
=
−
0
,
0331
{\displaystyle \scriptstyle h_{d}(-2)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle -2\times 1,4661\right)}{\scriptstyle -2\textstyle \pi }}\scriptstyle =-0,0331}
h
(
−
2
)
H
P
=
w
(
−
2
)
×
h
d
(
−
2
)
H
P
=
0
,
6199
×
−
0
,
0331
=
−
0
,
0205
{\displaystyle \scriptstyle h(-2)_{HP}=w(-2)\times h_{d}(-2)_{HP}=0,6199\times -0,0331=-0,0205}
-1
h
d
(
−
1
)
H
P
=
−
sin
(
−
1
×
1
,
4661
)
−
1
π
=
−
0
,
3166
{\displaystyle \scriptstyle h_{d}(-1)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle -1\times 1,4661\right)}{\scriptstyle -1\textstyle \pi }}\scriptstyle =-0,3166}
h
(
−
1
)
H
P
=
w
(
−
2
)
×
h
d
(
−
1
)
H
P
=
0
,
8924
×
−
0
,
3166
=
−
0
,
2825
{\displaystyle \scriptstyle h(-1)_{HP}=w(-2)\times h_{d}(-1)_{HP}=0,8924\times -0,3166=-0,2825}
0
h
d
(
0
)
H
P
=
1
−
2
×
f
c
=
1
−
2
×
0
,
2333
=
0
,
5334
{\displaystyle \scriptstyle h_{d}(0)_{HP}=1-2\times f_{c}=1-2\times 0,2333=0,5334}
h
(
0
)
H
P
=
w
(
0
)
×
h
d
(
0
)
H
P
=
1
,
0000
×
0
,
5334
=
0
,
5334
{\displaystyle \scriptstyle h(0)_{HP}=w(0)\times h_{d}(0)_{HP}=1,0000\times 0,5334=0,5334}
1
h
d
(
1
)
H
P
=
−
sin
(
1
×
1
,
4661
)
1
π
=
−
0
,
3166
{\displaystyle \scriptstyle h_{d}(1)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle 1\times 1,4661\right)}{\scriptstyle 1\textstyle \pi }}\scriptstyle =-0,3166}
h
(
1
)
H
P
=
w
(
1
)
×
h
d
(
1
)
H
P
=
0
,
8924
×
−
0
,
3166
=
−
0
,
2825
{\displaystyle \scriptstyle h(1)_{HP}=w(1)\times h_{d}(1)_{HP}=0,8924\times -0,3166=-0,2825}
2
h
d
(
2
)
H
P
=
−
sin
(
2
×
1
,
4661
)
2
π
=
−
0
,
0331
{\displaystyle \scriptstyle h_{d}(2)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle 2\times 1,4661\right)}{\scriptstyle 2\textstyle \pi }}\scriptstyle =-0,0331}
h
(
2
)
H
P
=
w
(
2
)
×
h
d
(
2
)
H
P
=
0
,
6199
×
−
0
,
0331
=
−
0
,
0205
{\displaystyle \scriptstyle h(2)_{HP}=w(2)\times h_{d}(2)_{HP}=0,6199\times -0,0331=-0,0205}
3
h
d
(
3
)
H
P
=
−
sin
(
3
×
1
,
4661
)
3
π
=
0
,
1009
{\displaystyle \scriptstyle h_{d}(3)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle 3\times 1,4661\right)}{\scriptstyle 3\textstyle \pi }}\scriptstyle =0,1009}
h
(
3
)
H
P
=
w
(
3
)
×
h
d
(
3
)
H
P
=
0
,
3100
×
0
,
1009
=
0
,
0313
{\displaystyle \scriptstyle h(3)_{HP}=w(3)\times h_{d}(3)_{HP}=0,3100\times 0,1009=0,0313}
4
h
d
(
4
)
H
P
=
−
sin
(
4
×
1
,
4661
)
4
π
=
0
,
0324
{\displaystyle \scriptstyle h_{d}(4)_{HP}=-\textstyle {\frac {\sin \left(\scriptstyle 4\times 1,4661\right)}{\scriptstyle 4\textstyle \pi }}\scriptstyle =0,0324}
h
(
4
)
H
P
=
w
(
4
)
×
h
d
(
4
)
H
P
=
0
,
1077
×
0
,
0324
=
0
,
0035
{\displaystyle \scriptstyle h(4)_{HP}=w(4)\times h_{d}(4)_{HP}=0,1077\times 0,0324=0,0035}
Filtro PasaBanda
f
b
=
f
b
p
−
Δ
F
/
2
=
10000
H
z
/
48000
H
z
−
0
,
3667
/
2
=
0
,
0250
{\displaystyle f_{b}=f_{bp}-\Delta F/2=10000Hz/48000Hz-0,3667/2=0,0250}
ω
b
=
2
π
f
b
=
0
,
1571
{\displaystyle \omega _{b}=2\pi f_{b}=0,1571}
f
a
=
f
a
p
+
Δ
F
/
2
=
14000
H
z
/
48000
H
z
+
0
,
367
/
2
=
0
,
4750
{\displaystyle f_{a}=f_{ap}+\Delta F/2=14000Hz/48000Hz+0,367/2=0,4750}
ω
a
=
2
π
f
a
=
2
,
9845
{\displaystyle \omega _{a}=2\pi f_{a}=2,9845}
Recuerdese que para efectos de identificación:
h
(
n
)
→
h
(
n
)
B
P
{\displaystyle \scriptstyle h(n)\;\rightarrow \;h(n)_{BP}}
h
d
(
n
)
→
h
d
(
n
)
B
P
{\displaystyle \scriptstyle h_{d}(n)\;\rightarrow \;h_{d}(n)_{BP}}
n
{\displaystyle n}
h
d
(
n
)
B
P
=
2
f
a
sin
(
n
×
ω
a
)
n
ω
a
−
2
f
b
sin
(
n
×
ω
b
)
n
ω
b
=
sin
(
n
×
ω
a
)
−
sin
(
n
×
ω
b
)
n
π
{\displaystyle \scriptstyle h_{d}(n)_{BP}=2\textstyle f_{a}{\frac {\sin \scriptstyle \left(n\times \omega _{a}\right)}{n\omega _{a}}}\scriptstyle -2\textstyle f_{b}{\frac {\sin \scriptstyle \left(n\times \omega _{b}\right)}{n\omega _{b}}}\scriptstyle =\textstyle {\frac {\sin \left(n\times \omega _{a}\right)-\sin \left(n\times \omega _{b}\right)}{n\pi }}}
h
(
n
)
B
P
=
w
(
n
)
×
h
d
(
n
)
B
P
{\displaystyle \scriptstyle h(n)_{BP}=w(n)\times h_{d}(n)_{BP}}
-4
h
d
(
−
4
)
B
P
=
sin
(
−
4
×
2
,
9845
)
−
sin
(
−
4
×
0
,
1571
)
−
4
π
=
−
0
,
0935
{\displaystyle \scriptstyle h_{d}(-4)_{BP}=\textstyle {\frac {\sin \left(-4\times 2,9845\right)-\sin \left(-4\times 0,1571\right)}{-4\pi }}\scriptstyle =-0,0935}
h
(
−
4
)
B
P
=
w
(
−
4
)
×
h
d
(
−
4
)
B
P
=
0
,
1077
×
−
0
,
0935
=
−
0
,
0101
{\displaystyle \scriptstyle h(-4)_{BP}=w(-4)\times h_{d}(-4)_{BP}=0,1077\times -0,0935=-0,0101}
-3
h
d
(
−
3
)
B
P
=
sin
(
−
3
×
2
,
9845
)
−
sin
(
−
3
×
0
,
1571
)
−
3
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(-3)_{BP}=\textstyle {\frac {\sin \left(-3\times 2,9845\right)-\sin \left(-3\times 0,1571\right)}{-3\pi }}\scriptstyle =0,0000}
h
(
−
3
)
B
P
=
w
(
−
3
)
×
h
d
(
−
3
)
B
P
=
0
,
3100
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(-3)_{BP}=w(-3)\times h_{d}(-3)_{BP}=0,3100\times 0,0000=0,0000}
-2
h
d
(
−
2
)
B
P
=
sin
(
−
2
×
2
,
9845
)
−
sin
(
−
2
×
0
,
1571
)
−
2
π
=
−
0
,
0984
{\displaystyle \scriptstyle h_{d}(-2)_{BP}=\textstyle {\frac {\sin \left(-2\times 2,9845\right)-\sin \left(-2\times 0,1571\right)}{-2\pi }}\scriptstyle =-0,0984}
h
(
−
2
)
B
P
=
w
(
−
2
)
×
h
d
(
−
2
)
B
P
=
0
,
6199
×
−
0
,
0984
=
−
0
,
0601
{\displaystyle \scriptstyle h(-2)_{BP}=w(-2)\times h_{d}(-2)_{BP}=0,6199\times -0,0984=-0,0601}
-1
h
d
(
−
1
)
B
P
=
sin
(
−
1
×
2
,
9845
)
−
sin
(
−
1
×
0
,
1571
)
−
1
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(-1)_{BP}=\textstyle {\frac {\sin \left(-1\times 2,9845\right)-\sin \left(-1\times 0,1571\right)}{-1\pi }}\scriptstyle =0,0000}
h
(
−
1
)
B
P
=
w
(
−
2
)
×
h
d
(
−
1
)
B
P
=
0
,
8924
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(-1)_{BP}=w(-2)\times h_{d}(-1)_{BP}=0,8924\times 0,0000=0,0000}
0
h
d
(
0
)
B
P
=
2
×
(
f
a
−
f
b
)
=
2
×
(
0
,
4750
−
0
,
0250
)
=
0
,
9000
{\displaystyle \scriptstyle h_{d}(0)_{BP}=2\times (f_{a}-f_{b})=2\times (0,4750-0,0250)=0,9000}
h
(
0
)
B
P
=
w
(
0
)
×
h
d
(
0
)
B
P
=
1
,
0000
×
0
,
9000
=
0
,
9000
{\displaystyle \scriptstyle h(0)_{BP}=w(0)\times h_{d}(0)_{BP}=1,0000\times 0,9000=0,9000}
1
h
d
(
1
)
B
P
=
sin
(
1
×
2
,
9845
)
−
sin
(
1
×
0
,
1571
)
1
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(1)_{BP}=\textstyle {\frac {\sin \left(1\times 2,9845\right)-\sin \left(1\times 0,1571\right)}{1\pi }}\scriptstyle =0,0000}
h
(
1
)
B
P
=
w
(
1
)
×
h
d
(
1
)
B
P
=
0
,
8924
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(1)_{BP}=w(1)\times h_{d}(1)_{BP}=0,8924\times 0,0000=0,0000}
2
h
d
(
2
)
B
P
=
sin
(
2
×
2
,
9845
)
−
sin
(
2
×
0
,
1571
)
2
π
=
−
0
,
0984
{\displaystyle \scriptstyle h_{d}(2)_{BP}=\textstyle {\frac {\sin \left(2\times 2,9845\right)-\sin \left(2\times 0,1571\right)}{2\pi }}\scriptstyle =-0,0984}
h
(
2
)
B
P
=
w
(
2
)
×
h
d
(
2
)
B
P
=
0
,
6199
×
−
0
,
0984
=
−
0
,
0601
{\displaystyle \scriptstyle h(2)_{BP}=w(2)\times h_{d}(2)_{BP}=0,6199\times -0,0984=-0,0601}
3
h
d
(
3
)
B
P
=
sin
(
3
×
2
,
9845
)
−
sin
(
3
×
0
,
1571
)
3
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(3)_{BP}=\textstyle {\frac {\sin \left(3\times 2,9845\right)-\sin \left(3\times 0,1571\right)}{3\pi }}\scriptstyle =0,0000}
h
(
3
)
B
P
=
w
(
3
)
×
h
d
(
3
)
B
P
=
0
,
3100
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(3)_{BP}=w(3)\times h_{d}(3)_{BP}=0,3100\times 0,0000=0,0000}
4
h
d
(
4
)
B
P
=
sin
(
4
×
2
,
9845
)
−
sin
(
4
×
0
,
1571
)
4
π
=
−
0
,
0935
{\displaystyle \scriptstyle h_{d}(4)_{BP}=\textstyle {\frac {\sin \left(4\times 2,9845\right)-\sin \left(4\times 0,1571\right)}{4\pi }}\scriptstyle =-0,0935}
h
(
4
)
B
P
=
w
(
4
)
×
h
d
(
4
)
B
P
=
0
,
1077
×
−
0
,
0935
=
−
0
,
0101
{\displaystyle \scriptstyle h(4)_{BP}=w(4)\times h_{d}(4)_{BP}=0,1077\times -0,0935=-0,0101}
Filtro ParaBanda
f
b
=
f
b
p
+
Δ
F
/
2
=
2000
H
z
/
48000
H
z
+
0
,
3667
/
2
=
0
,
2250
{\displaystyle f_{b}=f_{bp}+\Delta F/2=2000Hz/48000Hz+0,3667/2=0,2250}
ω
b
=
2
π
f
b
=
1
,
4137
{\displaystyle \omega _{b}=2\pi f_{b}=1,4137}
f
a
=
f
a
p
−
Δ
F
/
2
=
22000
H
z
/
48000
H
z
−
0
,
3667
/
2
=
0
,
2750
{\displaystyle f_{a}=f_{ap}-\Delta F/2=22000Hz/48000Hz-0,3667/2=0,2750}
ω
a
=
2
π
f
a
=
1
,
7279
{\displaystyle \omega _{a}=2\pi f_{a}=1,7279}
Recuerdese que para efectos de identificación:
h
(
n
)
→
h
(
n
)
B
S
{\displaystyle \scriptstyle h(n)\;\rightarrow \;h(n)_{BS}}
h
d
(
n
)
→
h
d
(
n
)
B
S
{\displaystyle \scriptstyle h_{d}(n)\;\rightarrow \;h_{d}(n)_{BS}}
n
{\displaystyle n}
h
d
(
n
)
B
S
=
2
f
b
sin
(
n
×
ω
b
)
n
ω
b
−
2
f
a
sin
(
n
×
ω
a
)
n
ω
a
=
sin
(
n
×
ω
b
)
−
sin
(
n
×
ω
a
)
n
π
{\displaystyle \scriptstyle h_{d}(n)_{BS}=2\textstyle f_{b}{\frac {\sin \scriptstyle \left(n\times \omega _{b}\right)}{n\omega _{b}}}\scriptstyle -2\textstyle f_{a}{\frac {\sin \scriptstyle \left(n\times \omega _{a}\right)}{n\omega _{a}}}\scriptstyle =\textstyle {\frac {\sin \left(n\times \omega _{b}\right)-\sin \left(n\times \omega _{a}\right)}{n\pi }}}
h
(
n
)
B
S
=
w
(
n
)
×
h
d
(
n
)
B
S
{\displaystyle \scriptstyle h(n)_{BS}=w(n)\times h_{d}(n)_{BS}}
-4
h
d
(
−
4
)
B
S
=
sin
(
−
4
×
1
,
4137
)
−
sin
(
−
4
×
1
,
7279
)
−
4
π
=
−
0
,
0935
{\displaystyle \scriptstyle h_{d}(-4)_{BS}=\textstyle {\frac {\sin \left(-4\times 1,4137\right)-\sin \left(-4\times 1,7279\right)}{-4\pi }}\scriptstyle =-0,0935}
h
(
−
4
)
B
S
=
w
(
−
4
)
×
h
d
(
−
4
)
B
S
=
0
,
1077
×
−
0
,
0935
=
−
0
,
0101
{\displaystyle \scriptstyle h(-4)_{BS}=w(-4)\times h_{d}(-4)_{BS}=0,1077\times -0,0935=-0,0101}
-3
h
d
(
−
3
)
B
S
=
sin
(
−
3
×
1
,
4137
)
−
sin
(
−
3
×
1
,
7279
)
−
3
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(-3)_{BS}=\textstyle {\frac {\sin \left(-3\times 1,4137\right)-\sin \left(-3\times 1,7279\right)}{-3\pi }}\scriptstyle =0,0000}
h
(
−
3
)
B
S
=
w
(
−
3
)
×
h
d
(
−
3
)
B
S
=
0
,
3100
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(-3)_{BS}=w(-3)\times h_{d}(-3)_{BS}=0,3100\times 0,0000=0,0000}
-2
h
d
(
−
2
)
B
S
=
sin
(
−
2
×
1
,
4137
)
−
sin
(
−
2
×
1
,
7279
)
−
2
π
=
0
,
0984
{\displaystyle \scriptstyle h_{d}(-2)_{BS}=\textstyle {\frac {\sin \left(-2\times 1,4137\right)-\sin \left(-2\times 1,7279\right)}{-2\pi }}\scriptstyle =0,0984}
h
(
−
2
)
B
S
=
w
(
−
2
)
×
h
d
(
−
2
)
B
S
=
0
,
6199
×
0
,
0984
=
0
,
0601
{\displaystyle \scriptstyle h(-2)_{BS}=w(-2)\times h_{d}(-2)_{BS}=0,6199\times 0,0984=0,0601}
-1
h
d
(
−
1
)
B
S
=
sin
(
−
1
×
1
,
4137
)
−
sin
(
−
1
×
1
,
7279
)
−
1
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(-1)_{BS}=\textstyle {\frac {\sin \left(-1\times 1,4137\right)-\sin \left(-1\times 1,7279\right)}{-1\pi }}\scriptstyle =0,0000}
h
(
−
1
)
B
S
=
w
(
−
2
)
×
h
d
(
−
1
)
B
S
=
0
,
8924
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(-1)_{BS}=w(-2)\times h_{d}(-1)_{BS}=0,8924\times 0,0000=0,0000}
0
h
d
(
0
)
B
S
=
1
−
2
×
(
f
a
−
f
b
)
=
1
−
2
×
(
1
,
7279
−
1
,
4137
)
=
0
,
9000
{\displaystyle \scriptstyle h_{d}(0)_{BS}=1-2\times (f_{a}-f_{b})=1-2\times (1,7279-1,4137)=0,9000}
h
(
0
)
B
S
=
w
(
0
)
×
h
d
(
0
)
B
S
=
1
,
0000
×
0
,
9000
=
0
,
9000
{\displaystyle \scriptstyle h(0)_{BS}=w(0)\times h_{d}(0)_{BS}=1,0000\times 0,9000=0,9000}
1
h
d
(
1
)
B
S
=
sin
(
1
×
1
,
4137
)
−
sin
(
1
×
1
,
7279
)
1
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(1)_{BS}=\textstyle {\frac {\sin \left(1\times 1,4137\right)-\sin \left(1\times 1,7279\right)}{1\pi }}\scriptstyle =0,0000}
h
(
1
)
B
S
=
w
(
1
)
×
h
d
(
1
)
B
S
=
0
,
8924
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(1)_{BS}=w(1)\times h_{d}(1)_{BS}=0,8924\times 0,0000=0,0000}
2
h
d
(
2
)
B
S
=
sin
(
2
×
1
,
4137
)
−
sin
(
2
×
1
,
7279
)
2
π
=
0
,
0984
{\displaystyle \scriptstyle h_{d}(2)_{BS}=\textstyle {\frac {\sin \left(2\times 1,4137\right)-\sin \left(2\times 1,7279\right)}{2\pi }}\scriptstyle =0,0984}
h
(
2
)
B
S
=
w
(
2
)
×
h
d
(
2
)
B
S
=
0
,
6199
×
0
,
0984
=
0
,
0601
{\displaystyle \scriptstyle h(2)_{BS}=w(2)\times h_{d}(2)_{BS}=0,6199\times 0,0984=0,0601}
3
h
d
(
3
)
B
S
=
sin
(
3
×
1
,
4137
)
−
sin
(
3
×
1
,
7279
)
3
π
=
0
,
0000
{\displaystyle \scriptstyle h_{d}(3)_{BS}=\textstyle {\frac {\sin \left(3\times 1,4137\right)-\sin \left(3\times 1,7279\right)}{3\pi }}\scriptstyle =0,0000}
h
(
3
)
B
S
=
w
(
3
)
×
h
d
(
3
)
B
S
=
0
,
3100
×
0
,
0000
=
0
,
0000
{\displaystyle \scriptstyle h(3)_{BS}=w(3)\times h_{d}(3)_{BS}=0,3100\times 0,0000=0,0000}
4
h
d
(
4
)
B
S
=
sin
(
4
×
1
,
4137
)
−
sin
(
4
×
1
,
7279
)
4
π
=
−
0
,
0935
{\displaystyle \scriptstyle h_{d}(4)_{BS}=\textstyle {\frac {\sin \left(4\times 1,4137\right)-\sin \left(4\times 1,7279\right)}{4\pi }}\scriptstyle =-0,0935}
h
(
4
)
B
S
=
w
(
4
)
×
h
d
(
4
)
B
S
=
0
,
1077
×
−
0
,
0935
=
−
0
,
0101
{\displaystyle \scriptstyle h(4)_{BS}=w(4)\times h_{d}(4)_{BS}=0,1077\times -0,0935=-0,0101}
Comentarios finales
En todo los procedimientos el valor de
n
{\displaystyle n}
−
(
N
−
1
)
/
2
{\displaystyle -(N-1)/2}
(
N
−
1
)
/
2
{\displaystyle (N-1)/2}
y
(
n
)
{\displaystyle y(n)}
n
{\displaystyle n}
h
(
n
)
{\displaystyle h(n)}
0
≤
n
≤
(
N
−
1
)
{\displaystyle \scriptstyle 0\leq n\leq (N-1)}
(
N
−
1
)
/
2
{\displaystyle (N-1)/2}
n
{\displaystyle n}
N
=
9
→
(
N
−
1
)
/
2
=
4
{\displaystyle \scriptstyle N=9\rightarrow (N-1)/2=4}
h
(
n
)
=
h
(
n
+
(
N
−
1
)
/
2
)
L
P
=
h
(
n
+
4
)
L
P
{\displaystyle \scriptstyle h(n)=h(n+(N-1)/2)_{LP}=h(n+4)_{LP}}
h
(
n
)
=
h
(
n
+
(
N
−
1
)
/
2
)
H
P
=
h
(
n
+
4
)
H
P
{\displaystyle \scriptstyle h(n)=h(n+(N-1)/2)_{HP}=h(n+4)_{HP}}
h
(
n
)
=
h
(
n
+
(
N
−
1
)
/
2
)
B
P
=
h
(
n
+
4
)
B
P
{\displaystyle \scriptstyle h(n)=h(n+(N-1)/2)_{BP}=h(n+4)_{BP}}
h
(
n
)
=
h
(
n
+
(
N
−
1
)
/
2
)
S
B
=
h
(
n
+
4
)
S
B
{\displaystyle \scriptstyle h(n)=h(n+(N-1)/2)_{SB}=h(n+4)_{SB}}





































![{\displaystyle \scriptstyle y(3)=x(3)*h(3)=x[0]h(3)+x(1)h(2)+x(2)h(1)+x(3)h(0)+x(4)h(-1)+x(5)h(-2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f2147f59cf62d5eea7e55b9de45c4c93fc21e78)













![{\displaystyle a(0)=h[(N-1)/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ec7ac97511a0dfd1413ed9a3ea38d37cfbde605)
![{\displaystyle a(n)=2h[(N-1)/2-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a80172ea9e70a86e4e0ae32340e4cea91e5e9c23)
![{\displaystyle b(n)=2h[N/2-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d24fff5ebd782f41ac09e19a8a037447c7847ff)



















































![{\displaystyle \scriptstyle {\frac {I_{o}\left[\beta {\sqrt {\left(1-\left({\frac {2n}{\left(N-1\right)}}\right)^{2}\right)}}\right]}{I_{o}\left(\beta \right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/887cd7d7d881e95339630039e6ae584bc20aa9fd)