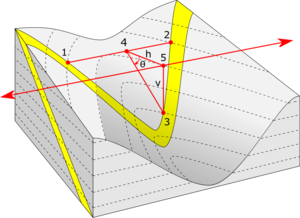
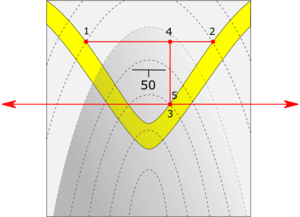
Problema de los tres puntos

El problema de los tres puntos o método de los tres puntos, es una técnica geométrica y trigonométrica que se usa para calcular el rumbo y buzamiento de estructuras geológicas homoclinales a partir de la ubicación y elevación de tres puntos sobre el afloramiento en un mapa topográfico.^[1]​^[2]​ Al aplicar este método, se asume que el buzamiento y el rumbo se mantienen relativamente constantes a lo largo de toda la estructura.

Se puede calcular el rumbo y buzamiento de estructuras geológicas como por ejemplos: estratos, capas, fracturas, contactos, diques, fallas, etc. Necesariamente se requiere de los tres puntos para determinar la orientación de un plano.^[1]​ Este método se puede usar de dos manera:^[1]​

1. Con dos puntos de igual elevación y uno diferente.

2. Con tres puntos de diferente elevación.

1. Dos puntos de igual elevación y uno diferente: este es el caso más sencillo, el cual consiste en ubicar dos puntos que tengan la misma altitud o cota contenida en el mismo contacto de afloramiento, de esta manera se dibuja una línea recta que pase por los dos puntos y se determina la dirección del rumbo del plano midiendo el ángulo que forma esta horizontal con el norte; una segunda línea de rumbo se traza paralela a la primera con el tercer punto localizado a una altitud diferente, esto ayuda para definir el buzamiento del plano, que podrá calcularse formando un ángulo al trazar una línea recta horizontal y perpendicular a las dos líneas de rumbo con una línea de máxima pendiente perpendicular a la primera línea de rumbo hasta el tercer punto.^[1]​^[2]​

• PROBLEMA DE LOS TRES PUNTOS
• 
  Vista Isométrica de un bloque con afloramiento de capa homoclinal río abajo.
• 
  Vista Superior del bloque con afloramiento de capa homoclinal río abajo.
• 
  Triángulo de los tres puntos: Tan θ = v/h

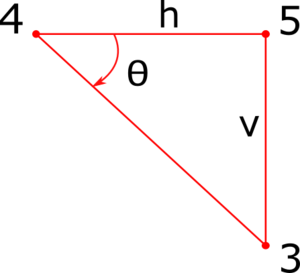
Utilizando la ecuación:

$${\displaystyle \tan \theta =v/h}$$Donde:

θ = ángulo de buzamiento

h = distancia horizontal

v = distancia vertical

2. Tres puntos de diferente elevación: se basa en la premisa geométrica que tres puntos no coliniales definen un plano. En este caso, se tiene un plano definido por tres puntos no coliniales que se hallan en cotas diferentes, una vez conocido estos puntos, se ubica otro punto a la misma cota de uno de los tres, y con estos dos puntos en la misma cota del plano, por definición se halla la línea de rumbo, que es una línea horizontal perteneciente al plano. Conociendo la línea de rumbo, se puede conocer la línea y el ángulo de buzamiento del plano usando el mismo procedimiento como se hace con los dos puntos de igual elevación y uno diferente.^[1]​

• Arellano, Javier., Romero, Rolando., Carreón, Marco., Villareal, Juan., Morales, Wendy., (2002). Ejercicios de Geología Estructural. Universidad Nacional Autónoma de México, Facultad de Ingeniería. p. 166.