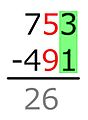
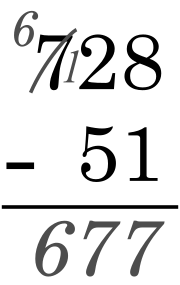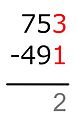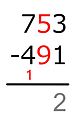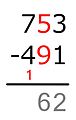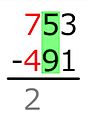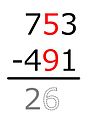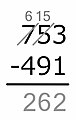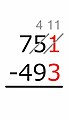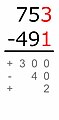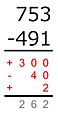Resta
|
Read other articles:

CongerRentang fosil: 55–0 jtyl PreЄ Є O S D C P T J K Pg N Eosen Awal sampai Saat Ini[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Anguilliformes Famili: Congridae Genus: CongerOken, 1817 Spesies Lihat teks. Anago (穴子, atau アナゴcode: ja is deprecated ) adalah kata Jepang untuk sidat air asin, biasanya merujuk kepada ma-anago (Conger myriaster). Ma-anago dipakai untuk hidangan makanan laut di Jepang. Mereka sering kali direbus (sus…

Peta menunjukkan lokasi Urbiztondo Data sensus penduduk di Urbiztondo Tahun Populasi Persentase 199535.746—200040.0892.49%200743.4301.11% Urbiztondo adalah munisipalitas yang terletak di provinsi Pangasinan, Filipina. Pada tahun 2010, munisipalitas ini memiliki populasi sebesar 46.000 jiwa dan 8.425 rumah tangga. Pembagian wilayah Secara administratif Urbiztondo terbagi menjadi 21 barangay, yaitu: Angatel Balangay Batangcaoa Baug Bayaoas Bituag Camambugan Dalangiring Duplac Galarin Gueteb Mala…

Penang Hindu Endowments BoardLembaga Wakaf Hindu Pulau Pinang பினாங்கு இந்து அறநிலைய வாரியம்Pemerintah Negara Bagian Penang[[File:|frameless]]Informasi State governmentDibentuk1 Januari 1906; 118 tahun lalu (1906-01-01)Kantor pusatLevel 30, Menara KOMTAR, 10000 Pulau Pinang.State government eksekutifYB Tuan RSN Rayer, DirekturState government indukPemerintah Negara Bagian PenangSitus webhebpenang.gov.my Dewan Wakaf Hindu Penang (Bahasa T…

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) لمعانٍ أخرى، طالع المثلث الذهبي (توضيح). المثلث الذهبي بمحافظة البحر الأحمر بالصحراء الشرقية المصري…

Sporting event delegationCyprus at the2004 Summer OlympicsIOC codeCYPNOCCyprus Olympic CommitteeWebsitewww.olympic.org.cy (in Greek and English)in AthensCompetitors20 in 7 sportsFlag bearer Georgios Achilleos[1]Medals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)198019841988199219962000200420082012201620202024 Cyprus competed at the 2004 Summer Olympics in Athens, Greece, from 13 to 29 August 2004. Athletics Main article: Athletics at the 2004 Summer O…

For related races, see 1896 United States gubernatorial elections. 1896 Vermont gubernatorial election ← 1894 September 1, 1896 (1896-09-01) 1898 → Nominee Josiah Grout J. Henry Jackson Party Republican Democratic Popular vote 53,426 14,855 Percentage 76.4% 21.2% Governor before election Urban A. Woodbury Republican Elected Governor Josiah Grout Republican Elections in Vermont Federal government Presidential elections 1792 1796 1800 1804 1808 1812…

French jet trainer aircraft CM.170 Magister A Magister of the Belgian Air Force Role Jet trainerType of aircraft National origin France Manufacturer Fouga, merged with Potez, merged with Sud-Aviation, merged with Aérospatiale First flight 23 July 1952 Introduction 1956 Status Retired; continues as civilian-owned warbirds Primary users French Air ForceIsraeli Air Force German Air Force Finnish Air Force Number built 929 total Air Fouga: 576 Heinkel-Messerschmitt: 194IAI: 36 Valmet: 62 Varia…

Set of laws implemented in Nazi Germany Eva Justin of the Racial Hygiene and Demographic Biology Research Unit measuring the skull of a Romani woman Part of a series onNazism Organizations Ahnenerbe Geheime Staatspolizei Deutsches Jungvolk Hitler Youth League of German Girls NSDÄB NSDStB NSRL NSFK NSKK NSF Nationalsozialistische Monatshefte Nazi Party Sturmabteilung (SA) Schutzstaffel (SS) History Early timeline National Socialist Program Hitler's rise to power Machtergreifung German rearmament…
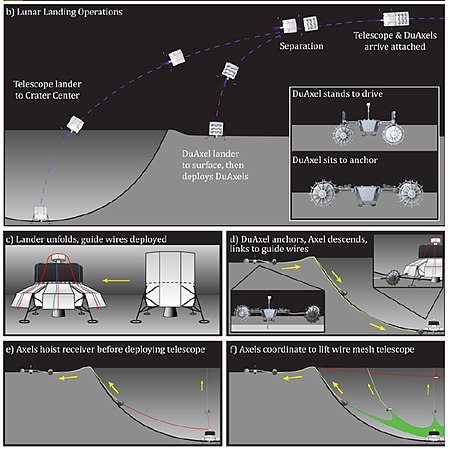
Proposed radio telescope Lunar Crater Radio TelescopeAlternative namesLCRT Location(s)far side of the MoonTelescope styleradio telescope Diameter350 m (1,148 ft 4 in) [edit on Wikidata] Concept of operations for building LCRT The Lunar Crater Radio Telescope (LCRT) is a proposal by the NASA Institute for Advanced Concepts (NIAC) to create an ultra-long-wavelength (that is, wavelengths greater than 10 m, corresponding to frequencies below 30 MHz) radio …
Caterina d'AragonaArtista sconosciuto, Caterina d'Aragona attorno al 1530, seconda metà del XVII secolo, olio su tavola, 55.9 x 44.5 cm, National Portrait Gallery, LondraRegina consorte d'InghilterraStemma In carica11 giugno 1509 –23 maggio 1533 Incoronazione24 giugno 1509 PredecessoreElisabetta di York SuccessoreAnna Bolena Principessa di GallesIn carica14 novembre 1501 –2 aprile 1502 Nome completoCaterina d'Aragona TrattamentoSua Maestà Altri titoliLady d'IrlandaInfanta d…

Chemical compound UlobetasolClinical dataTrade namesUltravateOther names(6S,8S,9S,10S,11S,13S,14S,16S,17R)-17-(2-Chloroacetyl)-6,9-difluoro-11,17-dihydroxy-10,13,16-trimethyl-6,7,8,11,12,14,15,16-octahydrocyclopenta[a]phenanthren-3-one, halobetasol (USAN US)AHFS/Drugs.comProfessional Drug FactsMedlinePlusa601060ATC codeD07AC21 (WHO) D05AX55 (WHO) (combination with tazarotene)Identifiers IUPAC name (6α,11β,16β)-21-Chloro-6,9-difluoro-11,17-dihydroxy-16-methylpregna-1,4-diene-3,2…

Ion Budai-DeleanuBorn(1760-01-06)January 6, 1760CigmăuDiedAugust 24, 1820(1820-08-24) (aged 60)Lemberg, Austrian EmpireOccupationHistorian, poet, scholar, philologistNationalityRomanianEducationUniversity of ViennaGenreEpic poemLiterary movementHumanismParentsSolomon Budai Ion Budai-Deleanu (January 6, 1760 – August 24, 1820)[1] was a Romanian scholar, philologist, historian, poet, and a representative of the Transylvanian School. Book cover of Tsiganiada ou le Campement des Tsig…

Poem by J.R.R Tolkien For the state of roving in search of chivalrous adventure, see knight-errant. Errantry is a three-page poem by J.R.R. Tolkien, first published in The Oxford Magazine in 1933.[T 1] It was included in revised and extended form in Tolkien's 1962 collection of short poems, The Adventures of Tom Bombadil. Donald Swann set the poem to music in his 1967 song cycle, The Road Goes Ever On. The poem has a complex metre, invented by Tolkien. It fits the tune of Gilbert and Sul…

English mathematician and philosopher (1861–1947) Alfred North WhiteheadOM FRS FBAWhitehead c. 1924Born(1861-02-15)15 February 1861Ramsgate, EnglandDied30 December 1947(1947-12-30) (aged 86)Cambridge, Massachusetts, U.S.EducationTrinity College, Cambridge(B.A., 1884)Era20th-century philosophyRegionWestern philosophySchoolAnalytic philosophy (early)Logicism (early)Process philosophyProcess theologyInstitutionsImperial College LondonHarvard UniversityAcademic advisorsEdward Routh …

Italian almond liqueur For other uses, see Amaretto (disambiguation). Not to be confused with amoretto or amaretti di Saronno. Bottles of amaretto liqueur Amaretto (Italian for 'a little bitter') is a sweet Italian liqueur originating from the comune (municipality) of Saronno. Depending on the brand, it may be made from apricot kernels, bitter almonds, peach stones, or almonds, all of which are natural sources of the benzaldehyde that provides the almond-like flavour of the liqueur.[1]&#…

FIFA Arab Cup 2021كأس العرب 2021Kaʾs al-ʿārab 2021Informasi turnamenTuan rumahQatarJadwalpenyelenggaraan30 November – 18 Desember 2021Jumlahtim peserta16 (dari 2 konfederasi)Tempatpenyelenggaraan6 (di 4 kota)← 2012 Piala Arab FIFA 2021 dijadwalkan akan edisi ke-10 dari dunia Arab. Tim nasional sepak bola turnamen ini akan menjadi edisi pertama dengan branding Piala Arab FIFA. Turnamen ini dijadwalkan berlangsung antara 30 November dan 18 Desember di Qatar, sebagai aw…

Upcoming Namma Metro station under Pink Line The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Tannery Road metro station – news · newspapers …

Хип-хоп Направление популярная музыка Истоки фанкдискоэлектронная музыкадабритм-энд-блюзреггидэнсхоллджаз[1]чтение нараспев[англ.]исполнение поэзииустная поэзияозначиваниедюжины[англ.]гриотыскэтразговорный блюз Время и место возникновения Начало 1970-х, Бронкс, Нь�…
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)[2…

P.S.F.K. Černomorec BurgasCalcio Segni distintiviUniformi di gara Casa Trasferta Colori sociali Blu, bianco Dati societariCittàBurgas Nazione Bulgaria ConfederazioneUEFA Federazione BFS Fondazione2005 Scioglimento2019StadioČernomorec(1 037 posti) PalmarèsSi invita a seguire il modello di voce Il Profesionalen Sporten Futbolen Klub Černomorec Burgas (in bulgaro Професионален спортен футболен клуб Черноморец Бургас?, Club sportivo…