|
Les Météores (Descartes)
Les Météores
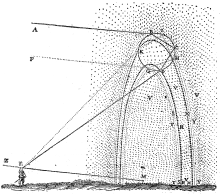 Les Météores sont l'un des trois essais publiés en 1637 par René Descartes conjointement au Discours de la Méthode. Les corpus de La Dioptrique, Les Météores et La Géométrie étaient destinés à montrer les résultats obtenus en suivant les préceptes de raison et de recherche de vérité dans les sciences énoncés dans la première partie de l'ouvrage. OrigineDans l'ensemble du Discours de la Méthode, alors que la préface donnait les indications générales, le traité des Météores était considéré par Descartes comme un sujet de philosophie pure, le traité de la Géométrie étant purement mathématique et la Dioptrique un mélange de philosophie et de mathématique[1]. Conçu entre 1629 et 1636, le traité des Météores comporte environ 80 pages et une cinquantaine d'illustrations dans l'édition de Leyde de 1637[2]. Cet écrit visait au départ à expliquer les parhélies observés à Rome le par son ami Henri Reneri qui lui demandait son avis sur le phénomène[3]. En 1633, la condamnation de Galilée par l'Inquisition porte un coup d'arrêt aux publications scientifiques de Descartes. Pendant l'impression de La Dioptrique, en 1635, Descartes finalise cependant les Météores et décide de l'ajouter au Discours de la Méthode[4]. Dans Les Météores, Descartes démontre qu'on peut traiter des phénomènes météorologiques de manière scientifique par l'observation, l'analyse et les mathématiques, en opposition aux traités de scolastique[5] qui considéraient des phénomènes comme le tonnerre, la grêle, les parhélies, , etc. comme des manifestations magiques. ContenuLes Météores est divisé en dix discours : De la nature des corps terrestres, Des vapeurs et des exhalaisons, Du sel, Des vents, Des nues, De la neige, de la pluie et de la grêle, Des tempêtes, de la foudre et de tous les autres feux qui s’allument en l’air, De l’arc-en-ciel, De la couleur des nues et des cercles ou couronnes qu’on voit quelquefois autour des astres, De l’apparition de plusieurs soleils. C'est dans le huitième discours du traité des Météores sur l'arc-en-ciel que Descartes donne une explication de ce phénomène fondée sur la physique mathématique. S'appuyant sur la loi de la réfraction énoncée dans la Dioptrique, Descartes étudie les rayons qui traversent une goutte d'eau théorique de forme sphérique. Il établit que l'arc-en-ciel principal, dont le rouge est dans la partie supérieure et le bleu dans la partie inférieure, est produit par des rayons réfractés en entrant dans la goutte d'eau puis réfléchis et réfractés à nouveau en quittant la goutte à un angle de 42° avec l'œil de l'observateur. L'arc-en-ciel secondaire, dont l'ordre des couleurs est inversé avec le bleu dans la partie supérieure et le rouge dans la partie inférieure, est produit par une réfraction des rayons à l'entrée de la goutte, une double réflexion à l'intérieur et une réfraction à la sortie. Les rayons forment un angle de 52° avec l'œil de l'observateur[6]. Si Descartes apporte des éléments à la théorie géométrique de l'arc-en-ciel, il peine à préciser la répartition et la largeur des bandes de couleurs de l'arc-en-ciel qui seront expliqués par Isaac Newton[7]. Notes et références
Bibliographie
Articles connexesLiens externes
|