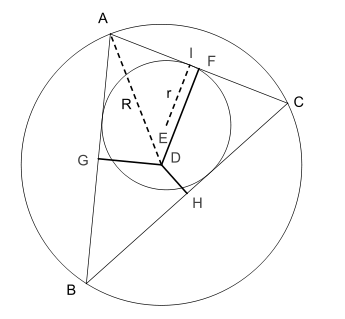
|
Théorème japonais de Carnot Pour les articles homonymes, voir Théorème de Carnot.  Ne doit pas être confondu avec Théorème japonais. Le théorème japonais de Carnot est un théorème de géométrie euclidienne dû à Lazare Nicolas Marguerite Carnot, portant sur une égalité algébrique de distances dans une construction faisant appel au cercle inscrit et au cercle circonscrit à un triangle[1],[2]. HistoireEn 1800, un samouraï anonyme accrochait au mur d'un temple une tablette de bois sur laquelle était gravé un sangaku, problème de géométrie dédié à une divinité (un kami) et proposé à la sagacité des fidèles. En 1803, Carnot publiait sa Géométrie de position. Hasard de l'Histoire, un théorème de cet ouvrage[3] permet de résoudre élégamment le sangaku précité. ÉnoncéThéorème de Carnot[4],[5],[6]. — Soit un triangle ABC et son cercle circonscrit de centre D et de rayon R. La somme des distances « signées » du centre D aux côtés du triangle est donnée par : où r est le rayon du cercle inscrit au triangle et F, G, H les projetés orthogonaux de D respectivement sur les côtés [AC], [AB] et [BC].
Notes et références
|
