Unicursale
|
Read other articles:

A Rose in the WindSingel oleh Anggundari album Snow on the SaharaDirilis1997FormatCD singleDirekam1996GenrePop, etnikDurasi4:27LabelSony MusicPenciptaErick Benzi, Nikki Matheson (Inggris), Anggun (Indonesia)ProduserErick Benzi A Rose in the Wind adalah sebuah lagu oleh penyanyi Indonesia Anggun dari album internasional pertamanya yang bertajuk Snow on the Sahara. Ini merupakan lagu pertama dalam karier Anggun yang direkam dalam tiga bahasa berbeda. Lagu ini aslinya diciptakan oleh Erick Benzi da…

Cara kerja katup jantung. Katup jantung adalah struktur tubuh yang memungkinkan cairan mengalir dalam tubuh, katup ini terdapat pada jantung.[1] Sedangkan menurut kamus kesehatan Katup jantung adalah jaringan khusus yang berada di dalam jantung yang tugasnya mengatur urutan aliran darah dari satu bagian ke bagian lain.[2] Katup ini dapat dibagi menjadi 2 yaitu katup aorta dan katup mitral.[2] Katup aorta ini adalah katup yang memisahkan ruang utama pemompa jantung (ventri…

Ini adalah nama Minahasa, marganya adalah Maramis. A. A. Maramis Menteri Keuangan Indonesia Ke-2Masa jabatan26 September 1945 – 14 November 1945PresidenSoekarno PendahuluSamsi SastrawidagdaPenggantiSoenarjo KolopakingMasa jabatan3 Juli 1947 – 29 Januari 1948PresidenSoekarnoPerdana MenteriAmir Sjarifuddin PendahuluSjafruddin PrawiranegaraPenggantiPetahanaMasa jabatan29 Januari 1948 – 19 Desember 1948PresidenSoekarnoPerdana MenteriMohammad Hatta PenggantiLukman…

Israel's ethnic and religious majority Israeli Jewsיהודים ישראליםTotal populationJewish citizens only:7,208,000 (73.2%)[1] Jews and non-Jewish relatives:7,762,000 (78.9%)Regions with significant populations Israel (incl. occupied territories) 7,181,000[a] United States500,000[6][7][8] Russia100,000 (80,000 in Moscow)[9][10] Canada10,755[11]–30,000[12&#…

Ballot initiative Proposal 3Add Voting Policies to ConstitutionResults Choice Votes % Yes 2,772,301 66.92% No 1,370,662 33.08% Valid votes 4,142,963 100.00% Invalid or blank votes 0 0.00% Total votes 4,142,963 100.00% Yes 80–90% 70–80% 60–70% 50–60% No 50–60% Source: MLive,[1] NYTimes[2] 2018 Michigan Proposal 3 (or just Proposal 3) was a ballot initiative approved by voters in Michigan as part of the 201…

Sayangi AisyahPemeran Wulan Guritno Adjie Pangestu Jessica Anastasya Mieke Wijaya Rima Melati Penggubah lagu temaDwiki DharmawanLagu pembukaSayangi Aku, Aisyah oleh Ita Purnamasari & Dwiki DharmawanLagu penutupSayangi Aku, Aisyah oleh Ita Purnamasari & Dwiki DharmawanPenata musikDwiki DharmawanNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode35ProduksiProduser eksekutifSoebagio SamtaniProduserGope T. SamtaniLokasi produksiJakartaPengaturan kameraMulti-kameraD…

Human social group For other uses, see Tribe (disambiguation). Tribal redirects here. For other uses, see Tribal (disambiguation). Tribals redirects here. For the ancient Thracian tribe, see Triballi. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced mat…
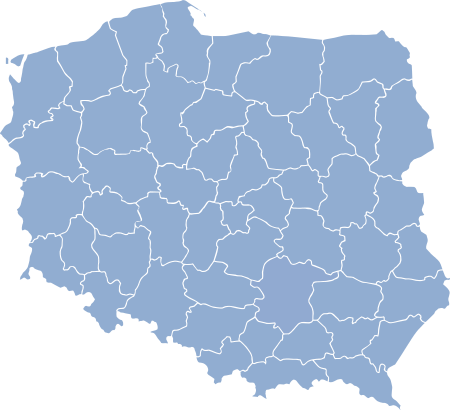
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ciechanów Voivodeship – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Ciechanów Voivodeship Ciechanów Voivodeship (Polish: województwo ciechanowskie) was a unit of administrative division and local government in…

1945 prototype multi-role combat aircraft by Henschel Hs 132 An airbrushed G. Heumann drawing of the P.132 Role Dive bomber and interceptor aircraftType of aircraft Manufacturer Henschel Flugzeugwerke AG Status Never flown Primary user Luftwaffe Produced 1945 Number built 4 prototypes[citation needed] The Henschel Hs 132 was a World War II dive bomber and interceptor aircraft of the German Luftwaffe that never saw service. The unorthodox design featured a top-mounted BMW 003 jet eng…

Pagoda BotataungAgamaAfiliasiTheravadaLokasiLokasiYangonNegaraMyanmarShown within MyanmarKoordinat16°46′06″N 96°10′19″E / 16.768449°N 96.171973°E / 16.768449; 96.171973Koordinat: 16°46′06″N 96°10′19″E / 16.768449°N 96.171973°E / 16.768449; 96.171973 Pagoda Botataung (Burma: ဗိုလ်တထောင်ဘုရားcode: my is deprecated ) adalah sebuah pagoda terkenal yang terletak di pusat kota Yangon, Myanmar, dekat…

Australian politician The HonourableWilliam GibsonMinister for Works and RailwaysIn office10 December 1928 – 22 October 1929Prime MinisterStanley BrucePreceded byWilliam HillSucceeded byJoseph LyonsPostmaster-General of AustraliaIn office5 February 1923 – 22 October 1929Prime MinisterStanley BrucePreceded byAlexander PoyntonSucceeded byJoseph LyonsDeputy Leader of the Country PartyIn office16 January 1923 – 19 November 1929LeaderEarle PagePreceded byWilliam Flemi…

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article's factual accuracy is disputed. Relevant discussion may be found on the talk page. Please help to ensure that disputed statements are reliably sourced. (September 2018) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this article by adding citations to reliab…

Marcus Grönholm Marcus Grönholm nel 2014 Nazionalità Finlandia Automobilismo Specialità Rally Carriera Carriera nel mondiale Rally Esordio Rally di Finlandia 1989 Stagioni 1989 - 2010 Scuderie Lancia, Toyota, SEAT, Mitsubishi, Peugeot, Ford, Subaru Mondiali vinti 2 (2000 e 2002) Rally disputati 153 Rally vinti 30 Podi 61 Punti ottenuti 615 Statistiche aggiornate al Rally di Svezia 2019 Modifica dati su Wikidata · Manuale Marcus Grönholm (Kauniainen, 5 febbraio 1968) è un ex…

Ираклеониты — ученики гностика Ираклеона (II век). Упоминаются как особая секта Епифанием и Августином; при крещении и миропомазании они соблюдали обряд помазания елеем и при этом произносили воззвания на арамейском языке, которые должны были освободить душу от власти �…

Massimo Maccarone Maccarone (a destra) nel 2010 Nazionalità Italia Altezza 180 cm Peso 70 kg Calcio Ruolo Allenatore (ex attaccante) Termine carriera 31 agosto 2020 - giocatore CarrieraGiovanili 1987-1988 Oleggio1988-1993 G.S. Soccer Boys1993-1998 MilanSquadre di club1 1997-1998 Milan0 (0)1998 Modena0 (0)1998-1999 Prato21 (4)[1]1999 Varese3 (0)1999-2000→ Prato28 (20)[2]2000-2002 Empoli68 (26)2002-2003 Middlesbrough57 (15)2004…

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) 土�…

Suburb of Sydney, New South Wales, AustraliaGirraweenSydney, New South WalesGirraween Public SchoolPopulation5,590 (2016 census)[1]Postcode(s)2145Elevation45 m (148 ft)Location30 km (19 mi) west of Sydney CBDLGA(s)Cumberland CouncilRegionWestern SydneyState electorate(s)ProspectFederal division(s)Greenway Suburbs around Girraween: Toongabbie Toongabbie Toongabbie Toongabbie Girraween Pendle Hill Pemulwuy Greystanes Greystanes Girraween is a suburb of Sydney,…

هذه المقالة عن هربرت فريدمان. لمعانٍ أخرى، طالع فريدمان (توضيح). هربرت فريدمان (بالإنجليزية: Herbert Friedman) معلومات شخصية الميلاد 21 يونيو 1916 بروكلين[1][2][3] الوفاة 9 سبتمبر 2000 (84 سنة) [4][5][3] مقاطعة أرلنغتون[6][1] سبب الوفاة سرطان…

جدارية وحدوية في بلفاست تحتفل بالفوز على منتخب إنجلترا لكرة القدم.[1] الرياضة تلعب دورًا هامًا في الهوية الوطنية في أيرلندا الشمالية. تٌعد مسألة اللعب كرة القدم يوم الأحد مسألة مثيرة للجدل في أيرلندا الشمالية. حتى عام 2008، قام الاتحاد الأيرلندي لكرة القدم تحت المادة 27،[2…

习近平 习近平自2012年出任中共中央总书记成为最高领导人期间,因其废除国家主席任期限制、开启总书记第三任期、集权统治、公共政策与理念、知识水平和自述经历等争议,被中国大陸及其他地区的民众以其争议事件、个人特征及姓名谐音创作负面称呼,用以恶搞、讽刺或批评习近平。对习近平的相关负面称呼在互联网上已经形成了一种活跃、独特的辱包亚文化。 权力類 �…


![{\displaystyle \left\{{\begin{array}{l}x=x_{0}+at\\[3pt]y=y_{0}+bt\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b89527d45adad85867cdc9ada6ba92b3966c977)


![{\displaystyle \left\{{\begin{array}{l}x={\dfrac {1-t^{2}}{1+t^{2}}}\\[3pt]y={\dfrac {2t}{1+t^{2}}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a133477b8a5a864b1769fb92134e10b09827813)



![{\displaystyle \left\{{\begin{array}{l}x={\dfrac {1+t^{2}}{1-t^{2}}}\\[3pt]y={\dfrac {2t}{1-t^{2}}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c91e39004297217ab1dcc1dd038de0a2e77de68f)
![{\displaystyle \left\{{\begin{array}{l}x={\dfrac {3t}{1+t^{3}}}\\[3pt]y={\dfrac {3t^{2}}{1+t^{3}}}.\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3e1276a9b2a66a7df5ed7e761d92eb26a732c1)



![{\displaystyle \left\{{\begin{array}{l}x=t^{2}\\[3pt]y=t^{3}.\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b091fc671cac61951e014b463a7f18ed9729c6b8)

![{\displaystyle \left\{{\begin{array}{l}x={\dfrac {2t}{1+t^{4}}}\\[3pt]y={\dfrac {2t^{3}}{1+t^{4}}}.\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ae0465e6970732ca45769a8932f23efa95d57f6)










![{\displaystyle \left\{{\begin{array}{l}x={\dfrac {1-5^{2}}{1+5^{2}}}={\dfrac {1-25}{1+25}}=-{\dfrac {24}{26}}=-{\dfrac {12}{13}}\\[4pt]y={\dfrac {2\times 5}{1+5^{2}}}={\dfrac {10}{1+25}}={\dfrac {5}{13}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e634ccf03621d1423fb198ffdbead2788f550a1)
