Isomorfismo
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Buku ilmu antik adalah karya sejarah asli, misalnya buku atau makalah teknis, tentang sains, matematika, dan kadang-kadang teknik. Buku-buku ini adalah rujukan utama yang penting untuk kajian sejarah sains dan teknologi, yang dapat memberikan wawasan berh…

Bushbuck tanjung Tragelaphus sylvaticus Bushbuck tanjung jantan di KenyaBushbuck tanjung betina di ZimbabweStatus konservasiRisiko rendah TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoArtiodactylaFamiliBovidaeGenusTragelaphusSpesiesTragelaphus sylvaticus Pallas, 1766 lbs Bushbuck tanjung (Tragelaphus sylvaticus) atau bushbuck adalah spesies antelop yang tersebar luas populasinya di Afrika Sub-Sahara. Untuk membedakan hewan ini dari kéwel (Tragelaphus scriptus) yang merupakan kerabat de…

Yang MuliaGiuseppe BetoriKardinal,Uskup Agung FirenzeGerejaGereja Katolik RomaKeuskupan agungFirenzeTakhtaFirenzePenunjukan8 September 2008Awal masa jabatan26 Oktober 2008PendahuluEnnio AntonelliJabatan lainKardinal-Imam San Marcello (2012-)ImamatTahbisan imam26 September 1970oleh Siro SilvestriTahbisan uskup6 Mei 2001oleh Camillo RuiniPelantikan kardinal18 Februari 2012oleh Paus Benediktus XVIPeringkatKardinal-imamInformasi pribadiNama lahirGiuseppe BetoriLahir25 Februari 1947 (umur&#…

Rumah Kelahiran Bung Hatta Istana Basa Paguruyung Pusat Dokumentasi dan Informasi KebudayaanMuseum Adityawarman Berikut ini adalah daftar museum di Sumatera Barat yang diurutkan abjad berdasarkan lokasi di setiap kabupatan/kota di Sumatera Barat. Kementerian Pendidikan dan Kebudayaan Berdasarkan data Kementerian Pendidikan dan Kebudayaan terdapat 12 museum di Sumatera Barat.[1] No Kode Pengelolaan Nama Museum Alamat Kecamatan Kabupaten/Kota 1 MS000118 Istano Basa Pagaruyung Nagari Pagaru…

Yesus, diyakini oleh umat Kristiani Mesias, sedangkan dalam kepercayaan umat Islam Yesus/Isa a.s adalah seorang Nabi dan Al-Masiyah(Mesias). Mesias (Ibrani: מָשִׁיחַ, translit: (māšîaḥ)code: he is deprecated ; Arab: مسيح, translit: (masîḥ)code: ar is deprecated ; Greek: μεσσίαςcode: el is deprecated , (messías)) berarti Yang Diurapi.[1] Sebutan Mesias berakar dari pengertian Yahudi mengenai seorang tokoh pada masa depan yang akan datang sebagai wakil…

Mayor of Los Angeles James R. TobermanPortrait of James Toberman,12th Mayor of Los AngelesIn officeDecember 5, 1872 – December 18, 1874Preceded byCristóbal AguilarSucceeded byPrudent BeaudryIn officeDecember 5, 1878 – December 9, 1882Preceded byBernard CohnSucceeded byCameron E. Thom Personal detailsBorn1836DiedJanuary 26, 1911(1911-01-26) (aged 74–75) James Ralph Toberman (1836 – January 26, 1911) served six one-year terms as Mayor of Los Angeles. He firs…

1938 film by Sidney Lanfield Always GoodbyeTheatrical release posterDirected bySidney LanfieldScreenplay by Kathryn Scola and Edith Skouras Based ona storyby Gilbert Emeryand Douglas DotyProduced byRaymond Griffith(associate producer)Starring Barbara Stanwyck Herbert Marshall Ian Hunter Cesar Romero Lynn Bari Binnie Barnes John Russell CinematographyRobert Planck, a.s.c.Edited byRobert SimpsonMusic byLouis Silvers(musical direction)ProductioncompanyTwentieth Century-Fox Film CorporationDistribut…
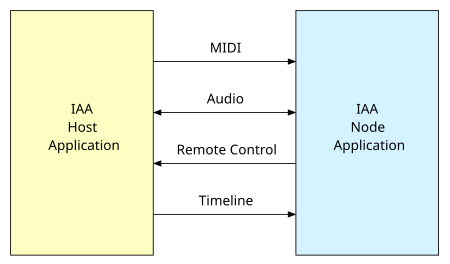
Inter-App Audio (IAA) is a deprecated[1] technology developed by Apple Inc. which routes audio and MIDI signals between applications on the iOS mobile operating system. The technology was first introduced in 2013 in iOS 7 and deprecated in 2019 with the release of iOS 13. Inter-App Audio Block Diagram Scope Inter-App Audio is a host-plugin technology. An IAA host application connects to a node application to send and receive audio, MIDI, timeline information, and other signals. Node appl…

Election 1971 Boston mayoral election ← 1967 November 2, 1971 1975 → Candidate Kevin White Louise Day Hicks Party Nonpartisan Nonpartisan Popular vote 113,137 70,331 Percentage 61.67% 38.33% Results by wardWhite: 50–60% 60–70% 70–80% 80–90% >90%Hicks: 50–60% Mayor before e…

Hironimus Rompas Makagansa Bupati Kepulauan SangiheMasa jabatan1 November 2011 – 28 Oktober 2016PresidenSusilo Bambang YudhoyonoJoko WidodoGubernurS.H. SarundajangOlly DondokambeyWakilJabes GaghanaPendahuluWinsulangi SalindehoPenggantiJabes GaghanaPj. Bupati Bolaang Mongondow UtaraMasa jabatan2007–2008PresidenSusilo Bambang YudhoyonoGubernurS.H. SarundajangPendahulutidak ada, jabatan baruPenggantiHamdan Datunsolang Informasi pribadiLahir5 Juni 1958 (umur 65)Sangihe, Sulawesi Ut…

Pour les articles homonymes, voir Malot. Hector MalotPortrait photographique d’Hector Malot par Nadar vers 1880.BiographieNaissance 20 mai 1830La BouilleDécès 18 juillet 1907 (à 77 ans)Avenue de la Dame-Blanche (Fontenay-sous-Bois)Sépulture Cimetière de Fontenay-sous-BoisNom de naissance Hector-Henri MalotSurnom Malot-la-ProbitéNationalité françaiseFormation Lycée Pierre-Corneille (1842-1847)Lycée Condorcet (1847-1849)Faculté de droit de Paris (1850-1853)Activités Romancier, a…

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、蘭&…

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Le ton de cet article ou de cette section est trop élogieux, voire hagiographique (mars 2022). Modifiez l'article pour adopter un ton neutre ou discutez-en. Ne doit pas être confondu avec Hermann Amandus Schwarz. Pour les articles homonymes, voir Laurent Schwartz et Schwartz. Laurent SchwartzLaurent Schwartz en 1970.FonctionPrésidentComité Maurice-Audin1960-1963Albert ChâteletBiographieNaissance 5 mars 191516e …

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁地�…
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)[2…

City in North Dakota, United StatesLisbon, North DakotaCityRansom County Courthouse in LisbonMotto: A Place to Call Home!Location of Lisbon, North DakotaCoordinates: 46°26′19″N 97°41′03″W / 46.43861°N 97.68417°W / 46.43861; -97.68417CountryUnited StatesStateNorth DakotaCountyRansomFounded1880Government • MayorTim MeyerArea[1] • Total2.29 sq mi (5.94 km2) • Land2.29 sq mi (5.94 km2)&…

Former metallurgical facility in Ukraine Azovstal redirects here. For other uses, see Azovstal (disambiguation). Azovstal Iron and Steel WorksAzovstal steel plant in 2014Native nameMеталургійний Kомбінат АзовстальCompany typePrivate, CombineTraded asPFTS: AZSTIndustrysteel productionFounded2 February 1930 (1930-02-02)Defunct20 May 2022FateDestroyed during the Siege of MariupolHeadquartersMariupol, UkraineKey peopleRinat Akhmetov, Enver Tskitishvili…

La Resurrección de Cristo, de Noël Coypel (1700), usando una representación ascendente de Jesús. La resurrección de Jesús es la creencia religiosa cristiana según la cual, después de haber sido condenado a muerte y ser crucificado,[1] Jesús fue resucitado de entre los muertos, como «primicias de los que durmieron» (1 Corintios 15:3-4),[2] siendo exaltado como Cristo (Mesías) y Señor.[3][4][5] En el Nuevo Testamento, después de que los romanos cruc…
Komando Resor Militer 172/Praja Wira YakthiDibentuk7 November 1976Negara IndonesiaCabangTNI Angkatan DaratTipe unitKorem Tipe APeranSatuan TeritorialBagian dariKodam XVII/CenderawasihMakoremJayapura, PapuaJulukanKorem 172/PWYPelindungTentara Nasional IndonesiaMotoMengobati dan Menyembuhkan Luka, Mengubur Dendam, Memperkuat KohesiBaret H I J A U Ulang tahun7 NovemberTokohKomandanBrigadir Jenderal TNI Dedi HardonoKepala StafKolonel Inf. Bobbie Triyantho, S.I.P. Komando Resor Militer…

معركة حصن بورتوفيق إستسلام القائد الإسرائيلي لنقطة بورتوفيق الحصينة بعد الموقعة 1973 معلومات عامة التاريخ 6 أكتوبر، 1973 الموقع سيناء، مصر النتيجة انتصار مصري وأستيلائها علي النقطة - أستسلام القوة الإسرائيلية المتحاربون مصر إسرائيل القادة صلاح عبد الحليمعلي المزاحي جا�…








