|
Lei de SnellEm ótica, a lei de Snell, ou simplesmente lei de refração, resume-se a uma expressão que dá o desvio angular sofrido por um raio de luz ao passar para um meio com índice de refração diferente do qual ele estava percorrendo. Em outras palavras, descreve a relação entre os ângulos de incidência e refração, quando referindo-se a luz ou outras ondas passando através de uma fronteira (interface) entre dois meios isotrópicos diferentes, tais como água e vidro. A lei de Snell-Descartes refere-se aos cientistas Willebrord Snellius e René Descartes. 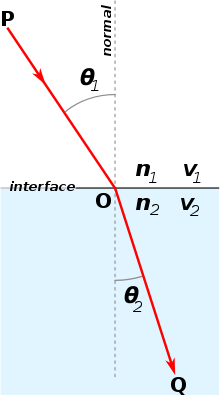 Para um raio de luz monocromática passando de um meio para o outro, é constante o produto do seno do ângulo, formado pelo raio e pela normal, com o índice de refração em que se encontra esse raio. Matematicamente:[1] em que e são os ângulos de incidência e refração, respectivamente, e e os índices de refração dos dois meios. Índice de refraçãoPara determinar o índice de refração () deve-se utilizar a expressão: Na qual:
ExplicaçãoA lei de Snell é usada para determinar a direção dos raios de luz através de meios refrativos com índices de refração distintos. Os índices de refração dos meios, , e assim por diante, são usados para representar o fator pelo qual a velocidade de um raio de luz diminui ao deslocar-se através de um meio refrativo, como vidro ou água, em oposição à sua velocidade no vácuo. Conforme a luz cruza a fronteira entre os meios, dependendo dos índices de refração relativos entre os dois, a luz poderá ser refratada para um ângulo menor ou maior. Esses ângulos são medidos com respeito à linha normal, representada perpendicularmente à fronteira. No caso onde luz desloca-se do ar para a água, a luz seria refratada em direção à linha normal, pois a velocidade da luz diminui na água; já a luz deslocando-se da água para o ar seria refratada na direção oposta á linha normal. A refração entre duas superfícies é denominada reversível pois se todas as condições forem idênticas, os ângulos seriam os mesmos para a luz movendo-se na direção oposta. A Lei de Snell é geralmente verdadeira somente para meios isotrópicos (como o vidro). Em meios anisotrópicos como alguns cristais, a birrefringência pode dividir o raio refratado em dois raios, o ordinário ou raio-o que segue a Lei de Snell, e o outro extraordinário ou raio-e que pode não ser coplanar ao raio incidente. Quando a luz ou outra onda envolvida é monocromática, isto é, frequência única, a Lei de Snell pode também ser expressa em termos de uma razão dos comprimentos de onda do raio em cada meio, λ1 e λ2: Derivações e fórmula A Lei de Snell pode ser derivada pelo princípio de Fermat,[2] que diz que a luz viaja pelo caminho que leva o menor tempo. Ao tomar a derivada do comprimento do caminho óptico, o ponto estacionário é encontrado, dando o caminho tomado pela luz (Embora deva-se ter em mente que o resultado não mostra a luz utilizando o caminho de menor tempo, mas sim o caminho que é estacionário para pequenas variações, de modo que há casos onde a luz na verdade toma o caminho que leva o maior tempo, como em um espelho esférico). Em uma analogia clássica, o meio de menor índice de refração pode ser visto como uma praia, e o de maior índice de refração como o oceano, e o modo mais rápido de um salva-vidas na praia chegar até uma pessoa no oceano é percorrendo o caminho que segue a Lei de Snell. Alternativamente, a Lei de Snell pode ser derivada utilizando a interferência de todos os caminhos possíveis da onda de luz da fonte até o observador—que resultam em interferência destrutiva em todos os pontos exceto no extremo da fase (onde a interferência será construtiva}— os quais tornam-se caminhos. Outra maneira de derivar a Lei de Snell envolve uma aplicação das condições gerais de contorno das equações de Maxwell para radiação eletromagnética. Ainda outra maneira de derivar a Lei de Snell é baseada em considerações de simetria de translação.[3] Por exemplo, uma superfície homogênea perpendicular à direção z não pode mudar o momento transverso. Já que o vetor de propagação é proporcional ao momento do fóton, a direção da propagação transversa deve permanecer a mesma em ambas as regiões. Presumindo sem perda de energia um plano de incidência no plano . Usando a dependência conhecida do número de onda no índice de refração do meio, derivamos a Lei de Snell. Sendo é o número de onda no vácuo. Perceba que nenhuma superfície é realmente homogênea, pelo menos em escala atômica. Ainda assim simetria translacional completa é uma excelente aproximação quando a região é homogênea na escala do comprimento de onda da luz. Forma vetorialDado um vetor de luz normalizado l (apontando da fonte de luz em direção à superfície) e um vetor normalizado do plano normal n, podemos encontrar os raios normalizados refletido e refratado:[4] Nota: deve ser positivo. Caso contrario, use Exemplo: Os cossenos podem ser reutilizados nas equações de Fresnel para encontrar a intensidade dos raios resultantes. A reflexão interna total é indicada por um radicando negativo na equação para . Nesse caso, uma onda evanescente é produzida, a qual decai rapidamente a partir da superfície e adentrando o segundo meio. A conservação de energia é mantida pela circulação da energia através da fronteira, em que a média da transmissão de energia de rede é zero. 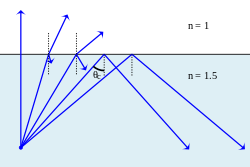 Reflexão interna total e ângulo críticoQuando a luz viaja de um meio com índice de refração maior para um com índice de refração menor, a Lei de Snell parece necessitar em alguns casos (quando o ângulo de incidência é suficientemente grande) que o seno do ângulo de refração seja maior que um. Isso claramente é impossível, e a luz nesses casos é completamente refletida pela fronteira, um fenômeno conhecido como reflexão interna total[5] O maior ângulo de incidência possível que ainda resulta em um raio refratado é chamado de ângulo crítico; nesse caso o raio refratado viaja ao longo da fronteira entre os dois meios. 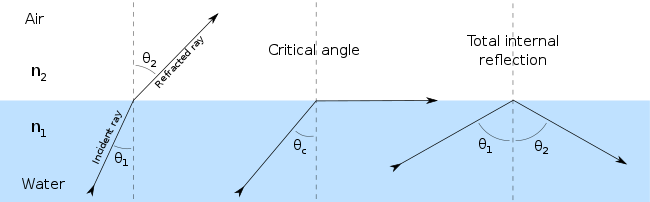 Por exemplo, considere um raio de luz movendo-se da água para o ar com um ângulo de incidência de 50°. Os índices de refração da água e do ar são aproximadamente 1.333 e 1, respectivamente, então a Lei de Snell nos dá a relação. A qual é impossível satisfazer. O ângulo crítico θcrit é o valor de θ1 para o qual θ2 é igual a 90°: DispersãoEm diversos meios propagadores de onda, a velocidade da onda muda conforme a frequência ou o comprimento de onda das ondas; Isso é verdadeiro para a propagação da luz na maioria dos meios transparentes, com exceção do vácuo. Esses meios são chamados de dispersivos. O resultado é que os ângulos determinados pela Lei de Snell também dependem da frequência e do comprimento de onda, de modo que um raio com comprimentos de ondas mistos, como a luz branca, irá se espalhar ou dispersar. Tal dispersão de luz no vidro ou na água oculta a origem dos arco-íris e de outros fenômenos ópticos, nos quais diferentes comprimentos de onda apresentam-se como diferentes cores. Em instrumentos ópticos, a dispersão leva à aberração cromática; um borrado dependente da cor que algumas vezes é efeito do limite de resolução. Isso ocorre especialmente em telescópios de refração, antes da invenção das lentes objetivas acromáticas. Meios condutores, absorvedores ou com perdasEm um meio condutor, a permissividade e o índice de refração são valores complexos. Consequentemente, o ângulo de refração e o vetor de onda também são. Isso implica que, enquanto as superfícies de uma fase real constante são planas cujas normais fazem um ângulo igual ao ângulo de refração com a normal da fronteira, as superfícies de amplitude constante, em contraste, são planos paralelos à própria fronteira. Como esses dois planos geralmente não coincidem, a onda é dita não-homogênea.[6] A onda refratada é exponencialmente atenuada, com expoente proporcional à componente imaginária do índice de refração.[7][8] Ver tambémReferências
|






























