Raiz quadrada de dois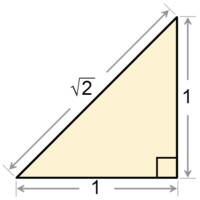

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW  • CAPES  • Google (notícias • livros • acadêmico)). (Junho de 2009)

A raiz quadrada de dois, denotada ${\displaystyle {\sqrt {2}}}$, é o único número real positivo cujo quadrado (ou seja, o resultado de sua multiplicação por si próprio) é dois: ${\displaystyle {\sqrt {2}}\times {\sqrt {2}}=2}$.

A raiz quadrada de dois é um número irracional,^{[1][Nota 1]} ou seja, não é possível encontrar dois números inteiros ${\displaystyle a}$ e ${\displaystyle b}$ tais que ${\displaystyle {\frac {a}{b}}={\sqrt {2}}.}$

Acredita-se que ${\displaystyle {\sqrt {2}}}$ tenha sido o primeiro número irracional reconhecido como tal. Esta importante descoberta é atribuída a Hipaso de Metaponto, da escola de Pitágoras. De acordo com uma lenda, a demonstração teria custado a vida de seu descobridor, uma vez que contrariava as ideias predominantes entre os pitagóricos de que tudo era número (inteiro).^[2]

Um triângulo retângulo cujos catetos medem 1 tem hipotenusa com comprimento ${\displaystyle {\sqrt {2}}}$.

A fração 9970 (≈ 1.4142857) por vezes é usada como uma boa aproximação racional com um denominador razoavelmente pequeno.

A sequência A002193 na Enciclopédia On-Line de Sequências Inteiras consiste nos dígitos da expansão decimal da raiz quadrada de 2, aqui truncada para 65 casas decimais:^[3]

1.41421356237309504880168872420969807856967187537694807317667973799

A raiz quadrada de dois pode ser escrita como:

• ${\displaystyle {\sqrt {2}}}$, lê-se "raiz quadrada de dois" ou "raiz de dois".
• ${\displaystyle 2^{\frac {1}{2}}}$ ou ${\displaystyle 2^{1/2}}$, lê-se "dois elevado a um meio" ou "dois a um meio".

Por ser um número irracional, ${\displaystyle {\sqrt {2}}}$ não pode ser expressa como um número finito de casas decimais, uma aproximação com 65 dígitos decimais é:

1,41421356237309504880168872420969807856967187537694807317667973799... (sequência A002193 na OEIS).

Uma aproximação fracionária para a raiz quadrada de 2 é 10/7 que, ao quadrado, fica 100/49, bem próximo de 2.

Pode-se facilmente construir uma sequência de números racionais se aproximando (convergindo) para ${\displaystyle {\sqrt {2}}}$:

${\displaystyle \left\{{\begin{array}{l}x_{0}=1\\x_{n+1}={\frac {x_{n}}{2}}+{\frac {1}{x_{n}}}\end{array}}\right.}$

Esta recursão produz a sequência:

${\displaystyle 1;~~{\frac {3}{2}};~~{\frac {17}{12}};~~{\frac {577}{408}};~~{\frac {665857}{470832}};~~{\frac {886731088897}{627013566048}}}$

Ou, aproximadamente:

${\displaystyle 1;~~1,5;~~1.416666667;~~1.414215686;~~1.414213562;~~1.414213562}$

Observe que o método estabiliza a nona casa decimal após apenas cinco passos.

O matemático britânico Godfrey Harold Hardy em seu livro Em defesa de um matemático afirma que a demonstração da irracionalidade da raiz quadrada de dois é um dos teoremas de "primeira classe". E que "conserva a beleza e o frescor que tinha ao ser descoberto" há mais de dois mil anos.

A demonstração é simples e recorre ao método da prova por contradição. Ou seja, supomos que exista um número racional igual a raiz de 2, ou seja, que existem números inteiros positivos ${\displaystyle a}$ e ${\displaystyle b}$ tais que:

${\displaystyle {\frac {a}{b}}={\sqrt {2}}}$

ou, equivalentemente:

${\displaystyle \left({\frac {a}{b}}\right)^{2}=2}$

Podemos supor que ${\displaystyle a}$ e ${\displaystyle b}$ não são ambos números pares, pois se fossem, poderíamos simplificar a fração até obter um dos termos da fração ímpar.

Agora, escrevemos:

${\displaystyle \left({\frac {a}{b}}\right)^{2}={\frac {a^{2}}{b^{2}}}=2}$

Então:

${\displaystyle a^{2}=2b^{2}}$

Concluímos então que ${\displaystyle a^{2}}$ deve ser um número par, pois é dobro de ${\displaystyle b^{2}}$. E ${\displaystyle a}$ deve ser par também, pois o quadrado de um número ímpar é ímpar.

Temos então que ${\displaystyle a}$ é um número par e, portanto, é o dobro de algum número inteiro, digamos ${\displaystyle c}$:

${\displaystyle a=2c}$

${\displaystyle (2c)^{2}=2b^{2}}$

${\displaystyle 4c^{2}=2b^{2}}$

${\displaystyle 2c^{2}=b^{2}}$

Pelos motivos alegados anteriormente, ${\displaystyle b}$ deve ser um número par.

Concluímos, finalmente, que se a raiz quadrada de 2 fosse um número racional, então este número seria uma fração que não tem forma irredutível, já que tanto o numerador quanto o denominador da fração são pares. Isto é um absurdo e, portanto, não existe um racional cujo quadrado seja igual a 2, como queríamos demonstrar.

Em 1786, o professor alemão de física Georg Christoph Lichtenberg^[4] descobriu que qualquer folha de papel cuja borda longa seja ${\displaystyle {\sqrt {2}}}$ vezes maior que sua borda curta poderia ser dobrada ao meio e alinhada com seu lado mais curto para produzir uma folha com exatamente as mesmas proporções como o original. Esta proporção de comprimentos do lado mais longo sobre o lado mais curto garante que o corte de uma folha ao meio ao longo de uma linha resulta em folhas menores tendo a mesma proporção (aproximada) da folha original. Quando a Alemanha padronizou os tamanhos de papel no início do século 20, eles usaram a proporção de Lichtenberg para criar a série "A" de tamanhos de papel.^[4] Hoje, a proporção (aproximada) dos tamanhos de papel em ISO 216 (A4, A0, etc.) é 1: ${\displaystyle {\sqrt {2}}}$

Existem algumas propriedades interessantes envolvendo a raiz quadrada de 2 nas ciências físicas:

• A raiz quadrada de dois é a razão de frequência de um intervalo de trítono em uma música de temperamento igual de doze tons.
• A raiz quadrada de dois forma a relação de f-stops em lentes fotográficas, o que, por sua vez, significa que a proporção das áreas entre duas aberturas sucessivas é 2.
• A latitude celestial (declinação) do Sol durante os pontos astronômicos de um quarto de dia cruzado é igual à inclinação do eixo do planeta dividido por ${\displaystyle {\sqrt {2}}}$

Notas e referências

Notas

Referências

• «Cinco milhões de casas decimais da raiz quadrada de 2» (em inglês) 

• Portal da matemática