|
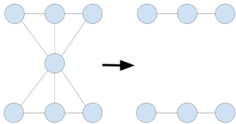
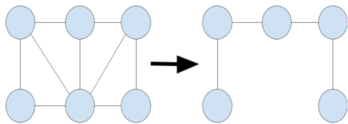
Tolerância a ataquesNo contexto da ciência das redes, a tolerância a ataques está relacionada com a robustez da rede. Isso significa que, na medida em que alguns nós da rede estão sendo removidos, ela consegue manter a sua conectividade e o seu diâmetro entre os nós restantes.[1] Caso a rede analisada seja em forma de estrela, por exemplo, quando ela sofrer algum ataque focado em nós com maior grau, ela pode ser “desconectada” totalmente arrancando somente 1 nó, mostrando que ela foi fragmentada, e que houve uma desconexão geral da rede. Esse exemplo pode ser visto na imagem ao lado. [carece de fontes]  DefiniçãoPara abordar a tolerância a ataques das redes, são estudadas as mudanças no diâmetro ou a conexão da rede, enquanto uma fração (entre 0 e 1) de nós é removida. Isso quer dizer que, quanto maior for o valor de , mais nós serão retirados na rede. Portanto, ao retirar ou danificar um nó, pode acarretar em um aumento da distância entre os nós restantes, pois durante essa ação, são eliminados alguns caminhos que contribuem para a conectividade interna da rede. Além disso, quando alguns nós são removidos da rede, “novos” clusters podem aparecer, pois os nós que ligavam esses clusters a um conjunto maior foram removidos, gerando assim uma fragmentação da rede.[2] Para uma melhor visualização dos dois efeitos, podemos olhar as duas imagens a seguir. A primeira mostra uma rede que se fragmenta quando é retirado o nó principal (nó de maior grau), que faz a ligação entre dois lados da rede. Depois de ser retirado, formam-se dois clusters. Já a outra imagem mostra o aumento do diâmetro da rede com a retirada de um nó. Imagem demonstrando uma rede sendo fragmentada em dois clusters. Imagem mostra uma rede que logo depois de uma retirada de um dos nós, o diâmetro da rede é aumentado. Dois métodos mais comuns para atacar uma rede são:
Tipos de redesComo foi dito na seção anterior, algumas redes se comportam diferente com um certo tipo de ataque. Portanto, a seguir serão mostrados alguns exemplos de redes e suas vulnerabilidades, todos os resultados estão mais detalhados no artigo citado.[2] Modelo livre de escalaNo modelo livre de escala, a rede tem seus graus definidos pela lei da potência, isso significa que, nessa rede, a maioria dos nós tem graus baixos, e a minoria dos nós (hubs) possuem graus altos.[3] Analisando mudança de diâmetroPara analisar o diâmetro foi utilizada uma rede livre de escala com 10000 (dez mil) nós e 20000 (vinte mil) ligações. Foi observado que, após a rede sofrer um ataque aleatório e perder 5% dos nós, o seu diâmetro não foi afetado, pois como a distribuição da lei da potência implica que a maioria dos nós possui apenas alguns links, isso faz com que nós com pequena conectividade sejam selecionados com uma probabilidade muito maior. Contudo, a remoção desses nós 'pequenos' não altera a estrutura do caminho dos nós restantes e, portanto, não tem impacto na topologia geral da rede.[2] Porém, quando a rede sofreu um ataque direcionado a nós com maior grau, a rede foi bastante danificada, pois, depois da retirada de 5% de nós, o diâmetro da rede aumentou tão rapidamente que chegou a ser duplicado. Isso se dá pelo fato da rede possuir poucos nós altamente conectados, cuja remoção altera drasticamente a topologia da rede e diminui a capacidade dos nós restantes de se comunicarem entre si.[2] Analisando desfragmentação da redePara esse teste foi observado o maior cluster de uma rede livre de escala, e quando ela foi atacada aleatoriamente por uma fração de , o tamanho desse cluster diminui lentamente, pois a maioria dos nós possuem poucos links, que, caso retirados, não modificam tanto o tamanho do maior cluster.[2] Entretanto, nos testes em que a rede sofreu um ataque direcionado a nós com maior grau, os nós mais significativos eram os pilares do maior cluster, e quando retirados, fizeram com que a rede fosse fragmentada. Isso mostra que essa rede é mais prejudicada por ataques em nós com maior grau.[2] Limite crítico sob ataqueNessa parte vamos analisar a fração crítica dessa rede. Para isso vamos analisar as duas consequências que acontecem nessa rede durante um ataque[1]:
Portanto, para quantificar esse processo, precisamos calcular analiticamente para uma rede sob ataque. Para fazer isso, contamos com o fato de que a remoção de hubs altera a rede de duas maneiras:
Combinando as duas mudanças acima, podemos observar um ataque com remoção aleatória de nós dessa rede, com e ajustados. Os cálculos prevêem que o limite crítico para ataques em uma rede livre de escala é a solução da equação abaixo: A equação acima mostra uma solução numérica em função do expoente de grau , permitindo-nos tirar várias conclusões a partir da equação encontrada:
Modelo Erdős–RényiEste tipo de rede gerada pode ser considerada como homogênea. Isso significa que, a maioria dos nós possuem aproximadamente o mesmo número de ligações.[4] Analisando mudança de diâmetroPara analisar o diâmetro foi utilizado uma rede homogênea com 10000 (dez mil) nós e 20000 (vinte mil) ligações. Foi observado que, para a rede exponencial, o diâmetro aumenta monotonicamente de acordo com que os nós são retirados (independentemente do tipo de ataque), portanto é cada vez mais difícil para os nós restantes se comunicarem entre si. Isso acontece pois todos os nós têm aproximadamente o mesmo número de links, todos contribuem igualmente para o diâmetro da rede, portanto, a remoção de cada nó causa a mesma quantidade de dano.[2] Analisando desfragmentação da redeComo já foi dito acima, o tipo de ataque não importa para essa rede, pois a maioria dos nós possui o mesmo número de links. Portanto, para analisar este fato, foi calculado o tamanho do maior cluster de uma rede homogênea, e enquanto ela sofria um ataque, foi notado que enquanto alguns nós foram retirados, o tamanho do maior cluster ficava diminuindo, formando clusters isolados, fazendo com que a rede rapidamente seja fragmentada em vários clusters.[2] Limite crítico sob ataqueConsiderando esse tipo de rede, podemos encontrar também o seu limite critico sob ataque . O seu limite critico pode ser encontrado utilizando a fórmula abaixo, considerando que e : Podemos notar através dessa fórmula que, quanto maior for o grau médio dos nós da rede, mais a rede está protegida por danos causados pelos ataques. Paul Baran e a internetEm 1959, Paul Baran, um jovem engenheiro da época, foi designado para desenvolver um sistema de comunicação que pudesse sobreviver a um ataque nuclear soviético. Como um ataque nuclear prejudica todo o equipamento dentro do alcance da detonação, Baran teve que projetar um sistema cujos usuários fora desse alcance não perdessem o contato uns com os outros. Ele descreveu a rede de comunicação de seu tempo como uma estrutura hierárquica de um conjunto de estrelas conectadas na forma de uma estrela maior, oferecendo uma descrição inicial do que chamamos hoje de rede sem escala. Ele concluiu que essa topologia é muito centralizada para ser viável sob ataque. Ele também descartou a topologia centralizada que é obviamente vulnerável, pois a destruição de um único nó central destrói a comunicação entre as estações finais.[1] Baran decidiu que a arquitetura de sobrevivência ideal era uma rede em malha distribuída. Esta rede é suficientemente redundante, de forma que mesmo se algum dos nós falhar, caminhos alternativos podem conectar os nós restantes. As ideias de Baran foram ignoradas pelos militares, então, quando a internet nasceu, uma década depois, ela dependia de protocolos distribuídos que permitiam que cada nó decidisse onde se conectar. Essa filosofia descentralizada pavimentou o caminho para o surgimento de uma internet sem escala, em vez da topologia em malha uniforme imaginada por Baran.[1] Referências
|