För andra betydelser, se Volym (olika betydelser) . Volym är mätetalet för mängden tredimensionell rymd som omges av slutna gränser, till exempel, det utrymme som en substans (fast, flytande, gas eller plasma) eller form upptar eller innehåller.[ 1]
SI-enheten för volym är kubikmeter , m 3 . Liter (l ) kan också härledas: 1 l = 0,001 m 3 .
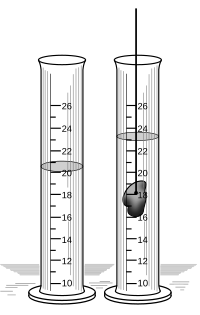
Ett sätt att bestämma volym
Objekt
Volym
Parametrar
Kub
a
3
{\displaystyle a^{3}\;}
a är längden hos kubens sidor
Cylinder
π
r
2
h
{\displaystyle \pi r^{2}h\;}
r är cylinderns radie, h är cylinderns höjd
Prisma
A
⋅
h
{\displaystyle A\cdot h}
A är basens area, h är prismans höjd
Rätblock
b
⋅
d
⋅
h
{\displaystyle b\cdot d\cdot h}
b är bredden, d är djupet och h är rätblockets höjd
Sfär
4
3
π
r
3
{\displaystyle {\frac {4}{3}}\pi r^{3}}
r är sfärens radie
Ellipsoid
4
3
π
a
b
c
{\displaystyle {\frac {4}{3}}\pi a\,b\,c}
a , b och c är ellipsoidradiernas längder
Pyramid
1
3
A
h
{\displaystyle {\frac {1}{3}}Ah}
A är basens area, h är pyramidens höjd
Kon
1
3
π
r
2
h
{\displaystyle {\frac {1}{3}}\pi \,r^{2}h}
r är cirkelbasens radie, h är spetsens avstånd till basen
Tetraeder
2
12
a
3
{\displaystyle {{\sqrt {2}} \over 12}a^{3}\,}
a är kantens längd
Parallellepiped
a
b
c
K
{\displaystyle a\,b\,c{\sqrt {K}}}
K
=
1
+
2
cos
(
α
)
cos
(
β
)
cos
(
γ
)
−
cos
2
(
α
)
−
cos
2
(
β
)
−
cos
2
(
γ
)
{\displaystyle {\begin{aligned}K=&1+2\cos(\alpha )\cos(\beta )\cos(\gamma )\\&-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\end{aligned}}}
a , b och c är parallellepipedens kantlängder. α, β, och γ är de interna vinklarna mellan dess kanter
Kleinflaska
0
{\displaystyle 0\;}
Ingen volym, då den inte har någon insida
Volym inom infinitesimalkalkyl
Inom infinitesimalkalkylen , ges volymen av ett område D i R 3 av trippelintegraler av den konstanta funktionen
f
(
x
,
y
,
z
)
=
1
{\displaystyle f(x,y,z)=1}
∭
D
1
d
x
d
y
d
z
.
{\displaystyle \iiint \limits _{D}1\,dx\,dy\,dz.}
Volymintegralen i cylindriska koordinater är
∭
D
r
d
r
d
θ
d
z
,
{\displaystyle \iiint \limits _{D}r\,dr\,d\theta \,dz,}
och volymintegralen i sfäriska koordinater (med användning av vinkelkonventionen med
θ
{\displaystyle \theta }
azimutala orienteringen och med
ϕ
{\displaystyle \phi }
∭
D
r
2
sin
ϕ
d
r
d
θ
d
ϕ
{\displaystyle \iiint \limits _{D}r^{2}\sin \phi \ dr\,d\theta \,d\phi }
där r är en punkts avstånd till origo .
Referenser