|
Драбина (теорія графів)
В теорії графів драбина Ln — планарний неорієнтований граф з 2n вершинами і n+2(n-1) ребрами . Драбину можна отримати прямим добутком двох шляхів, один з яких має тільки одне ребро — Ln,1 = Pn × P1 [1][2]. Якщо додати ще два ребра, що перетинаються і з'єднують чотири вершини драбини зі степенем два, одержимо кубічний граф — драбину Мебіуса. З побудови, драбина Ln ізоморфна решітці G2,n і виглядає як драбина з n щаблями. Граф є гамільтоновим з охопленням 4 (якщо n>1) і хроматичним індексом 3 (якщо n>2). Хроматичне число драбини дорівнює 2, а її хроматичний многочлен дорівнює . Кільцевий драбинний графКільцевий драбинний граф CLn — це прямий добуток циклу довжини n≥3 і ребра[3]. В символьному вигляді CLn = Cn × P1. Граф має 2n вершин і 3n ребер. Подібно до драбини граф є зв'язним, планарним і гамільтоновим, але граф є двочастковим тоді й лише тоді, коли n парне. Кільцевий драбинний граф — це багатогранний граф призм, тому його частіше називають графом призми. Кільцеві драбинні графи:
Драбина МебіусаЗ'єднавши чотири вершини степеня 2 «навхрест», отримаємо кубічний граф, який називають драбиною Мебіуса.  Галерея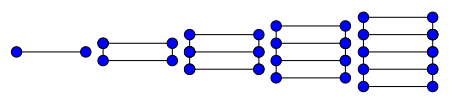
Примітки
Література
|
||||||||||||||||||||||








