Правило Тіциуса — Боде

Правило Тіциуса — Боде
Названо на честь	Йоганн Данієль Тіціус і Йоганн Елерт Боде
Вимірюється в	астрономічна одиниця
Правило Тіциуса — Боде у Вікісховищі

Правило Тіциуса — Боде (також відоме як закон Боде) — емпірична формула, яка приблизно описує відстані між планетами Сонячної системи і Сонцем (середні радіуси орбіт). Правило було запропоноване Йоганном Тіциусом у 1766 році й здобуло популярність завдяки роботам Йоганна Боде в 1772 році.

Правило формулюється таким чином:

Послідовність ${\displaystyle D_{i}}$ — геометрична прогресія, окрім першого числа. Тобто ${\displaystyle D_{1}=0;D_{i}=3\cdot 2^{i},i\geqslant 0}$

Цю ж формулу можна записати по-іншому:

${\displaystyle R_{1}=0.4,R_{i}=0.4+0.3\cdot 2^{i}}$.

Зустрічається також інше формулювання:

Результати обчислень приведені в таблиці (де ${\displaystyle k_{i}=D_{i}/3=0,1,2,4...}$). Видно, що цій закономірності відповідає і пояс астероїдів, а Нептун, навпаки, із закономірності випадає, причому його місце займає Плутон, хоча він, згідно з рішенням XXVI Асамблеї МАС, виключений з числа планет.

Планета	${\displaystyle i}$	${\displaystyle k_{i}}$	Радіус орбіти (а. о.)		${\displaystyle {R_{i}-R_{Mercury}} \over {R_{i-1}-R_{Mercury}}}$
			за правилом	фактичний
Меркурій	${\displaystyle -\infty }$	0	0,4	0,39
Венера	0	1	0,7	0,72
Земля	1	2	1,0	1,00	1,825
Марс	2	4	1,6	1,52	1,855
Пояс астероїдів	3	8	2,8	у середн. 2,2-3,6	2,096 (по орбіті Церери)
Юпітер	4	16	5,2	5,20	2,021
Сатурн	5	32	10,0	9,54	1,9
Уран	6	64	19,6	19,22	2,053
Нептун	випадає			30,06	1,579
Плутон	7	128	38,8	39,5	2,078 (по відношенню до Урана)
Ерида	8	256	77,2	67,7

Коли Тіциус уперше сформулював це правило, йому задовольняли усі відомі у той час планети (від Меркурія до Сатурна), був лише пропуск на місці п'ятої планети. Проте, правило не притягнуло великої уваги до тих пір, поки в 1781 року не був відкритий Уран, який майже точно ліг на передбачену послідовність. Після цього Боде призвав почати пошуки забраклої планети між Марсом і Юпітером. Саме у тому місці, де повинна була розташовуватися ця планета, була виявлена Церера. Це викликало велику довіру до правила Тіциуса — Боде серед астрономів, яке зберігалося до відкриття Нептуна. Коли з'ясувалося, що, окрім Церери, приблизно на тій же відстані від Сонця знаходиться безліч тіл, що формують пояс астероїдів, була висунена гіпотеза, що вони утворилися в результаті руйнування планети (Фаетона), яка раніше знаходилася на цій орбіті.

Правило не має конкретного математичного й аналітичного (через формули) пояснення, заснованого тільки на теорії гравітації, оскільки не існує загального рішення так званої «задачі трьох тіл» (у простому випадку), або «задачі N тіл» (у загальному випадку). Пряме чисельне моделювання також ускладнене величезним об'ємом обчислень.

Одне з вірогідних пояснень правила полягає в наступному. Вже на стадії формування Сонячної системи в результаті гравітаційних збурень, викликаних протопланетами і їх резонансом з Сонцем (при цьому виникають припливні сили і енергія обертання витрачається на припливне прискорення або швидше уповільнення) сформувалася регулярна структура з областей, що чергуються, в яких могли або не могли існувати стабільні орбіти згідно з правилами орбітальних резонансів (тобто відношення радіусів орбіт сусідніх планет рівних 1/2, 3/2, 5/2, 3/7 тощо)^[1], Утім, частина астрофізиків вважає, що це правило — усього лише випадковий збіг.

Резонансним орбітам зараз в основному відповідають планети або групи не розташовані на стабільних орбітах (як Нептун) і не розташовані в площині екліптики (як Плутон) напевно в найближчому (відносно сотень мільйонів років) минулому мали місце інциденти, орбіти (зіткнення, близький проліт масивного зовнішнього тіла), що порушували їх. З часом (швидше до центру системи і повільніше на околицях системи) вони неминуче займуть стабільні орбіти, якщо їм не завадять нові інциденти.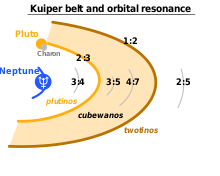

Наявність стабільних орбіт, викликаних резонансами між тілами системи, уперше чисельно змодельовано (комп'ютерна симуляція руху точкових взаємодійних мас навколо резонансного центра — Сонця, представленого як дві точкових маси з пружним зв'язком) і наведено порівняно з реальними астрономічними даними в роботах 1998—1999 років професора Рену Малхотра.

Саме існування резонансних орбіт і саме явище орбітального резонансу в нашій планетній системі підтверджується експериментальними даними по розподілу астероїдів по радіусу орбіти і щільності об'єктів KBO пояса Койпера по радіусу їх орбіти.

Порівнюючи структуру стабільних орбіт планет Сонячної системи з електронними оболонками простого атома, можна виявити деяку подібність, хоча в атомі перехід електрона відбувається практично миттєво тільки між стабільними орбітами (електронними оболонками), а в планетарній системі вихід небесного тіла на стабільні орбіти займає десятки і сотні мільйонів років.

Три планети Сонячної системи — Юпітер, Сатурн і Уран — мають систему супутників, які, можливо, сформувалися в результаті таких же процесів, як і у разі самих планет. Ці системи супутників утворюють регулярні структури, на основі орбітальних резонансів, які, правда, не підкоряються правилу Тіциуса — Боде в його первинному виді. Проте, як з'ясував у 1960-ті роки астроном Стенлі Дермотт, якщо трохи узагальнити правило Тіциуса — Боде:

${\displaystyle T(n)=T(0)\cdot C^{n}}$, ${\displaystyle \scriptstyle n=1,2,3,4\ldots }$

де ${\displaystyle T}$ — орбітальний період (днів), то нова формула з хорошою точністю охоплює системи супутників Юпітера, Сатурна й Урана (див. закон Дермотта^[fr]):

• Юпітер: T (0) = 0,444, C = 2,03

• Сатурн: T (0) = 0,462, C = 1,59

• Уран: T (0) = 0,488, C = 2,24

Тімоті Боверд (англ. Timothy Bovaird) і Чарльз Лайнвивер (англ. Charles H. Lineweaver) з Австралійського національного університету перевірили^[2] застосовність правила до екзопланетних систем (2013 рік). З відомих систем, що містять по чотири відкриті планети, вони відібрали 27 таких, для яких додавання додаткових планет між відомими, порушувало б стабільність системи. Вважаючи відібрані кандидати повними системами, автори показали, що для них виконується узагальнене правило Тіциуса — Боде, аналогічне запропонованому Дермоттом:

${\displaystyle R_{i}=R\cdot C^{i},i=0,1,2,3,...}$,

де R і C — параметри, що забезпечують найкраще наближення до спостережуваного розподілу.

Було виявлено, що з 27 відібраних для аналізу систем, 22 системи задовольняють взаємним співвідношенням радіусів орбіт навіть краще, ніж Сонячна система, 2 системи підходять під правило приблизно як Сонячна, у 3 систем правило працює гірше за Сонячну.

Для 64 систем, які за вибраним критерієм не були повними, автори спробували передбачити орбіти ще не відкритих планет. Всього ними зроблено 62 пророцтва за допомогою інтерполяції (у 25 системах) і 64 — за допомогою екстраполяції. Оцінка максимальних мас планет, зроблена по чутливості приладів, за допомогою яких були відкриті ці системи екзопланет, показує, що деякі з передбачених планет мають бути земного типу.

Згідно з перевіркою Chelsea X. Huang і Gáspár Á. Bakos (2014 р.) для екзопланет співвідношення Тіциуса — Боде в середньому не працює і, таким чином, його сила, що передбачає, під знаком питання^[3].

• Robert J. Sawyer. Golden Fleece, 1990

• Історія астрономії
• Історія відкриття планет і супутників Сонячної системи
• Планетологія
• Фаетон (планета)

• Ньето М. Закон Тициуса-Боде. Історія і теорія. М.: Світ, 1976.
• Планетарні орбіти і протон. «Наука і життя» № 1, 1993.
• Hahn, J.M., Malhotra, R. Orbital evolution of planets embedded in a massive planetesimal disk, AJ 117 : 3041-3053 (1999)
• Malhotra, R. Migrating Planets, Scientific American 281 (3) : 56-63 (1999)
• Malhotra, R. Chaotic planet formation, Nature 402 : 599—600 (1999)
• Malhotra, R. Orbital resonances and chaos in the Solar system, in Solar System Formation and Evolution, Rio de Janeiro, Brazil, ASP Conference Series vol. 149 (1998). Preprint
• Showman, A., Malhotra, R. The Galilean Satellites, Science 286 : 77 (1999)

• Правило XVIII століття у більшості планетарних систем виконується краще, ніж в Сонячній
• ^{[недоступне посилання з червня 2019}. Malhotra's research spans orbital dynamics in the solar system and in extra — solar planetary systems]^{[недоступне посилання з жовтня 2019]}(англ.)
• ^{[недоступне посилання з липня 2019} presentations/09-migrating planets.mov Анімація]^{[недоступне посилання з жовтня 2019]} На цій сторінці наводяться графіки розподілу астероїдів по орбітах і графіки розподілу плутино.(англ.)