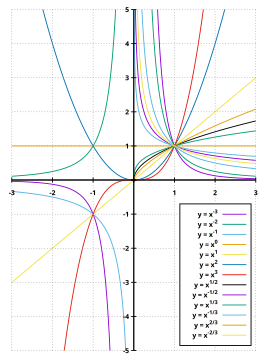
Степенева функція
Частково збігається з	polynomial functiond
Степенева функція у Вікісховищі

Степене́ва функція — функція вигляду ${\displaystyle f(x)=x^{a}\!\ }$, де a — показник степеню, дійсне число.

Область визначення: ${\displaystyle (0,\infty )}$ при ${\displaystyle a<0}$, ${\displaystyle [0,\infty )}$ при ${\displaystyle a>0}$.

При натуральних показниках степеня ${\displaystyle a}$ область визначення розширюється на всю числову вісь: ${\displaystyle (-\infty ,\infty )}$.

Область значень: ${\displaystyle (0,\infty )}$ при ${\displaystyle a<0}$, ${\displaystyle [0,\infty )}$ при ${\displaystyle a>0}$.

Монотонно спадає при ${\displaystyle a<0}$, монотонно зростає при ${\displaystyle a>0}$. При а > 0 функція має єдиний нуль в точці x= 0. Точок перетину не має.

При ${\displaystyle a<0}$ має особливу точку при ${\displaystyle x=0}$.

Похідна

${\displaystyle \left(x^{a}\right)^{\prime }=ax^{a-1}}$

Невизначений інтеграл

${\displaystyle \int x^{a}dx={\frac {x^{a+1}}{a+1}}+C}$

Степенева функція комплексного аргументу

${\displaystyle f(z)=z^{a}\,}$

аналітична (голоморфна) всюди, окрім точки z = 0 при нецілих значеннях показника ${\displaystyle a}$.

При раціональному показнику ${\displaystyle a=p/q}$, де ${\displaystyle p}$ та ${\displaystyle q}$ — цілі числа, функція визначається на рімановій поверхні із q листів, розріз проводиться вздовж півосі ${\displaystyle x={\text{Re }}\ z>0}$.

Таким чином, якщо скористатися представленням комплексного числа в експоненційній формі,

${\displaystyle z=re^{i\varphi }\,}$,

то ${\displaystyle \varphi }$ змінюється від 0 до ${\displaystyle 2\pi q}$.

${\displaystyle f(z)=z^{a}=r^{a}e^{ip\varphi /q}\,}$.

Для дійсного a — кількість ріманових листів безмежна.

• Аналітичне продовження

• Основні елементарні функції // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 177. — 594 с.
• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)

Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути піддано сумніву та вилучено. (червень 2014)

Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її.