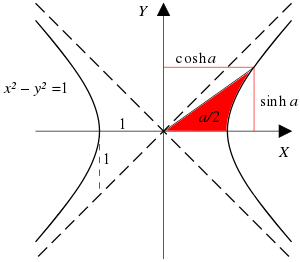
Một tia qua đường hyperbol đơn vị
x
2
−
y
2
=
1
{\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}
(
cosh
a
,
sinh
a
)
{\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}
a
{\displaystyle \scriptstyle a}
x
{\displaystyle \scriptstyle x}
Hàm hyperbolic ngược Trong toán học , hàm hyperbolic ngược hay hàm hyperbolic nghịch đảo là hàm ngược của hàm hyperbolic .
Cho một giá trị của hàm hyperbolic, ta được một hàm hyperbolic ngược tương ứng với một góc hyperbolic tương ứng. Độ lớn góc hyperbolic tương ứng sẽ bằng diện tích của vùng hyperbolic tương ứng của một đường hyperbol xy = 1đường hyperbola đơn vị x 2 − y 2 = 1góc tròn gấp hai lần diện tích của hình quạt tròn của đường tròn đơn vị . Nhiều tác giả đã gọi hàm hyperbolic ngược là "hàm diện tích " để nhận ra góc hyperbolic.[ 1] [ 2] [ 3] [ 4] [ 5] [ 6] [ 7] [ 8]
Hàm hyperbolic và ngược của chúng diễn ra trong nhiều phương trình vi phân tuyến tính, ví dụ như có phương trình được định nghĩa là đường dây xích , của một vài phương trình bậc ba , tính toán góc và khoảng cách trong hình học hyperbol và phương trình Laplace trong hệ tọa độ Descartes . Phương trình Laplace rất quan trọng trong nhiều lĩnh vực của vật lý , bao gồm điện từ học , trao đổi nhiệt , động lực học chất lưu , và thuyết tương đối hẹp .
Hàm hyperbolic là hàm phân thức của e x e x công thức bậc hai ; sau đó, lấy logarit tự nhiên cho biểu thức là hàm ngược hyperbolic.
Với số phức , hàm hyperbolic ngược, căn bậc hai và logarit là hàm đa trị , và đẳng thức tiếp theo được xem như là đẳng thức của hàm đa trị.
Cho tất cả những hàm hyperbolic ngược ngoài trừ hàm coth và hàm csch, tập xác định của hàm thực là tập hợp liên thông .
Hàm sinh ngược hay hàm sinh diện tích :
arsinh
x
=
ln
(
x
+
x
2
+
1
)
{\displaystyle \operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}
Tập xác định là số thực .
Hàm cosh ngược hay hàm cosh diện tích :
arcosh
x
=
ln
(
x
+
x
2
−
1
)
{\displaystyle \operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)}
Tập xác định là khoảng [1, +∞ ) .
Hàm tanh ngược hay hàm tanh diện tích :
artanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)}
Tập xác định là khoảng (−1, 1) .
Hàm coth ngược hay hàm coth diện tích :
arcoth
x
=
1
2
ln
(
x
+
1
x
−
1
)
{\displaystyle \operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)}
Tập xác định là phép hợp giữa khoảng (−∞, −1) và khoảng (1, +∞) .
Hàm sech ngược hay hàm sech diện tích :
arsech
x
=
ln
(
1
x
+
1
x
2
−
1
)
=
ln
(
1
+
1
−
x
2
x
)
{\displaystyle \operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)}
Tập xác định là khoảng (0, 1] .
Hàm csch ngược hay hàm csch diện tích :
arcsch
x
=
ln
(
1
x
+
1
x
2
+
1
)
{\displaystyle \operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)}
Tập xác định là số thực ngoại trừ 0.
arsinh
u
±
arsinh
v
=
arsinh
(
u
1
+
v
2
±
v
1
+
u
2
)
{\displaystyle \operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)}
arcosh
u
±
arcosh
v
=
arcosh
(
u
v
±
(
u
2
−
1
)
(
v
2
−
1
)
)
{\displaystyle \operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)}
artanh
u
±
artanh
v
=
artanh
(
u
±
v
1
±
u
v
)
{\displaystyle \operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)}
arsinh
u
+
arcosh
v
=
arsinh
(
u
v
+
(
1
+
u
2
)
(
v
2
−
1
)
)
=
arcosh
(
v
1
+
u
2
+
u
v
2
−
1
)
{\displaystyle {\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}}
2
arcosh
x
=
arcosh
(
2
x
2
−
1
)
với
x
≥
1
4
arcosh
x
=
arcosh
(
8
x
4
−
8
x
2
+
1
)
với
x
≥
1
2
arsinh
x
=
arcosh
(
2
x
2
+
1
)
với
x
≥
0
4
arsinh
x
=
arcosh
(
8
x
4
+
8
x
2
+
1
)
với
x
≥
0
{\displaystyle {\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ với }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ với }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ với }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ với }}x\geq 0\end{aligned}}}
ln
(
x
)
=
arcosh
(
x
2
+
1
2
x
)
=
arsinh
(
x
2
−
1
2
x
)
=
artanh
(
x
2
−
1
x
2
+
1
)
{\displaystyle \ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)}
sinh
(
arcosh
x
)
=
x
2
−
1
với
|
x
|
>
1
sinh
(
artanh
x
)
=
x
1
−
x
2
với
−
1
<
x
<
1
cosh
(
arsinh
x
)
=
1
+
x
2
cosh
(
artanh
x
)
=
1
1
−
x
2
với
−
1
<
x
<
1
tanh
(
arsinh
x
)
=
x
1
+
x
2
tanh
(
arcosh
x
)
=
x
2
−
1
x
với
|
x
|
>
1
{\displaystyle {\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{với}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{với}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{với}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{với}}\quad |x|>1\end{aligned}}}
arsinh
(
tan
α
)
=
artanh
(
sin
α
)
=
ln
(
1
+
sin
α
cos
α
)
=
±
arcosh
(
1
cos
α
)
{\displaystyle \operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)}
ln
(
|
tan
α
|
)
=
−
artanh
(
cos
2
α
)
{\displaystyle \ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)}
[ 9]
ln
x
=
artanh
(
x
2
−
1
x
2
+
1
)
=
arsinh
(
x
2
−
1
2
x
)
=
±
arcosh
(
x
2
+
1
2
x
)
{\displaystyle \ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)}
artanh
x
=
arsinh
(
x
1
−
x
2
)
=
±
arcosh
(
1
1
−
x
2
)
{\displaystyle \operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)}
arsinh
x
=
artanh
(
x
1
+
x
2
)
=
±
arcosh
(
1
+
x
2
)
{\displaystyle \operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)}
arcosh
x
=
|
arsinh
(
x
2
−
1
)
|
=
|
artanh
(
x
2
−
1
x
)
|
{\displaystyle \operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|}
d
d
x
arsinh
x
=
1
x
2
+
1
,
với mọi số thực
x
d
d
x
arcosh
x
=
1
x
2
−
1
,
với mọi số thực
x
>
1
d
d
x
artanh
x
=
1
1
−
x
2
,
với mọi số thực
|
x
|
<
1
d
d
x
arcoth
x
=
1
1
−
x
2
,
với mọi số thực
|
x
|
>
1
d
d
x
arsech
x
=
−
1
x
1
−
x
2
,
với mọi số thực
x
∈
(
0
,
1
)
d
d
x
arcsch
x
=
−
1
|
x
|
1
+
x
2
,
với mọi số thực
x
, ngoại trừ
0
{\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ với mọi số thực }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ với mọi số thực }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ với mọi số thực }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ với mọi số thực }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ với mọi số thực }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ với mọi số thực }}x{\text{, ngoại trừ }}0\\\end{aligned}}}
Ví dụ vi phân: cho θ = arsinh x , vậy (khi sinh2 θ = (sinh θ )2 ):
d
arsinh
x
d
x
=
d
θ
d
sinh
θ
=
1
cosh
θ
=
1
1
+
sinh
2
θ
=
1
1
+
x
2
.
{\displaystyle {\frac {d\,\operatorname {arsinh} x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1+\sinh ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.}
Biểu thức sau đây có thể được khai triển:
arsinh
x
=
x
−
(
1
2
)
x
3
3
+
(
1
⋅
3
2
⋅
4
)
x
5
5
−
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
7
7
±
⋯
=
∑
n
=
0
∞
(
(
−
1
)
n
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
2
n
+
1
2
n
+
1
,
|
x
|
<
1
{\displaystyle {\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}
arcosh
x
=
ln
(
2
x
)
−
(
(
1
2
)
x
−
2
2
+
(
1
⋅
3
2
⋅
4
)
x
−
4
4
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
−
6
6
+
⋯
)
=
ln
(
2
x
)
−
∑
n
=
1
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
−
2
n
2
n
,
|
x
|
>
1
{\displaystyle {\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}}
artanh
x
=
x
+
x
3
3
+
x
5
5
+
x
7
7
+
⋯
=
∑
n
=
0
∞
x
2
n
+
1
2
n
+
1
,
|
x
|
<
1
{\displaystyle {\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}
arcsch
x
=
arsinh
1
x
=
x
−
1
−
(
1
2
)
x
−
3
3
+
(
1
⋅
3
2
⋅
4
)
x
−
5
5
−
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
−
7
7
±
⋯
=
∑
n
=
0
∞
(
(
−
1
)
n
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
−
(
2
n
+
1
)
2
n
+
1
,
|
x
|
>
1
{\displaystyle {\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}
arsech
x
=
arcosh
1
x
=
ln
2
x
−
(
(
1
2
)
x
2
2
+
(
1
⋅
3
2
⋅
4
)
x
4
4
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
6
6
+
⋯
)
=
ln
2
x
−
∑
n
=
1
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
2
n
2
n
,
0
<
x
≤
1
{\displaystyle {\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}}
arcoth
x
=
artanh
1
x
=
x
−
1
+
x
−
3
3
+
x
−
5
5
+
x
−
7
7
+
⋯
=
∑
n
=
0
∞
x
−
(
2
n
+
1
)
2
n
+
1
,
|
x
|
>
1
{\displaystyle {\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}
Khai triển tiệm cận cho hàm arsinh x được cho bởi
arsinh
x
=
ln
(
2
x
)
+
∑
n
=
1
∞
(
−
1
)
n
−
1
(
2
n
−
1
)
!
!
2
n
(
2
n
)
!
!
1
x
2
n
{\displaystyle \operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}}
^ Bronshtein, Ilja N.; Semendyayev, Konstantin A.; Musiol, Gerhard; Mühlig, Heiner (2007). “Chapter 2.10: Area Functions”. Handbook of Mathematics Springer-Verlag . tr. 91 . doi :10.1007/978-3-540-72122-2 . ISBN 3-540-72121-5 ^ Ebner, Dieter (ngày 25 tháng 7 năm 2005). Preparatory Course in Mathematics (PDF) (ấn bản thứ 6). Department of Physics, University of Konstanz. Bản gốc (PDF) lưu trữ ngày 26 tháng 7 năm 2017. Truy cập ngày 26 tháng 7 năm 2017 . ^ Mejlbro, Leif (2006). Real Functions in One Variable – Calculus (PDF) . 1a (ấn bản thứ 1). Ventus Publishing ApS / Bookboon. ISBN 87-7681-117-4 Bản gốc (PDF) lưu trữ ngày 26 tháng 7 năm 2017. Truy cập ngày 26 tháng 7 năm 2017 . ^ Mejlbro, Leif (2008). The Argument Principle and Many-valued Functions - Complex Functions Examples (PDF) . c-9 (ấn bản thứ 1). Ventus Publishing ApS / Bookboon. ISBN 978-87-7681-395-6 Bản gốc (PDF) lưu trữ ngày 26 tháng 7 năm 2017. Truy cập ngày 26 tháng 7 năm 2017 . ^ Mejlbro, Leif (ngày 11 tháng 11 năm 2010). Stability, Riemann Surfaces, Conformal Mappings - Complex Functions Theory (PDF) . a-3 (ấn bản thứ 1). Ventus Publishing ApS / Bookboon. ISBN 978-87-7681-702-2 ISBN 87-7681-702-4 . Bản gốc (PDF) lưu trữ ngày 26 tháng 7 năm 2017. Truy cập ngày 26 tháng 7 năm 2017 . ^ Durán, Mario (2012). Mathematical methods for wave propagation in science and engineering . 1: Fundamentals (ấn bản thứ 1). Ediciones UC. tr. 89. ISBN 978-956141314-6 ISBN 956141314-0 . ^ Weltner, Klaus; John, Sebastian; Weber, Wolfgang J.; Schuster, Peter; Grosjean, Jean (ngày 27 tháng 6 năm 2014) [2009]. Mathematics for Physicists and Engineers: Fundamentals and Interactive Study Guide Springer-Verlag . ISBN 978-364254124-7 ISBN 3642541240 . ^ Detlef Reimers http://tug.ctan.org/macros/latex/contrib/lapdf/fplot.pdf
^ “Identities with inverse hyperbolic and trigonometric functions” . math stackexchange . stackexchange. Truy cập ngày 3 tháng 11 năm 2016 .
Herbert Busemann and Paul J. Kelly (1953) Projective Geometry and Projective Metrics , page 207, Academic Press .