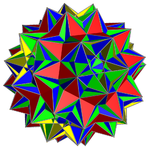
大二重扭稜二重斜方十二面體 又稱為斯基林立體 或斯基林圖形 (skilling's figure)是一種退化的非凸均勻多面體 ,由204個面和60個頂點組成。大二重扭稜二重斜方十二面體可透過將大二重斜方截半二十面體 與二十複合正八面體 異或 (或稱混合)來構造。[ 1]
除了無限集合的柱體 、反柱體 外,均勻多面體 僅有75種,這些多面體的列表在1954年首次發表[ 2] [ 3] 均勻多面體 。其令均勻多面體的邊可以重複、非單一之後,發現了一種退化之非凸均勻多面體的例子,即大二重扭稜二重斜方十二面體。更精確地說,在斯基林的研究中,其允許每條邊能有任意數量的相鄰面,並且確保這組面不會分成2個或以上的不相連集合,即這個立體不會是複合多面體 [ 4] [ 5] 斯基林立體 或斯基林圖 (skilling's figure),類似的立體還有米勒的怪物 [ 6] :259 [ 7] [ 8] :233 。
大二重扭稜二重斜方十二面體是一種退化的均勻多面體 ,其存在重合的邊,或與四個面相鄰的邊[ 9] :138 ,因此不被視為嚴格的均勻多面體[ 10] [ 11] 面 、240條邊 和60個頂點 組成[ 4] [ 11] [ 4] [ 1] [ 13]
在大二重扭稜二重斜方十二面體的204個面中,有120個正三角形 、60個正方形和24個五角星。在其60個頂點中,每個頂點都是6個三角形、4個正方形和2個五角星的公共頂點,並且這些面在頂角周圍依照五角星、正方形、三角形、三角形、三角形、正方形、反向相接的五角星、正方形、反向相接的三角形、反向相接的三角形、反向相接的三角形和正方形的順序排列,且圍繞頂角兩圈,這種頂角結構在頂點圖 中可以用(5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2 來表示。
大二重扭稜二重斜方十二面體的邊長為二的平方根 倍的外接球半徑[ 4] :122 ,這同時也意味著邊長為1的大二重扭稜二重斜方十二面體其外接球半徑為:[ 1]
1
2
≈
0.707107
{\displaystyle {\frac {1}{\sqrt {2}}}\approx 0.707107}
大二重扭稜二重斜方十二面體與大二重斜方截半二十面體 共用相同的頂點排列,也就是說在相同外接球的情況下,大二重扭稜二重斜方十二面體的頂點座標與大二重斜方截半二十面體 的頂點座標相同[ 14] [ 15]
(
±
5
−
1
−
2
5
−
2
8
,
±
3
−
5
−
10
5
−
22
8
,
±
2
+
2
5
−
2
8
)
,
{\displaystyle \left(\pm {\sqrt {\frac {{\sqrt {5}}-1-2{\sqrt {{\sqrt {5}}-2}}}{8}}},\,\pm {\sqrt {\frac {3-{\sqrt {5}}-{\sqrt {10{\sqrt {5}}-22}}}{8}}},\,\pm {\sqrt {\frac {2+{\sqrt {2{\sqrt {5}}-2}}}{8}}}\right),}
(
0
,
±
3
−
5
2
,
±
5
−
1
2
)
,
{\displaystyle \left(0,\,\pm {\frac {\sqrt {3-{\sqrt {5}}}}{2}},\,\pm {\frac {\sqrt {{\sqrt {5}}-1}}{2}}\right),}
(
±
3
−
5
+
10
5
−
22
8
,
±
2
−
2
5
−
2
8
,
±
5
−
1
+
2
5
−
2
8
)
.
{\displaystyle \left(\pm {\sqrt {\frac {3-{\sqrt {5}}+{\sqrt {10{\sqrt {5}}-22}}}{8}}},\,\pm {\sqrt {\frac {2-{\sqrt {2{\sqrt {5}}-2}}}{8}}},\,\pm {\sqrt {\frac {{\sqrt {5}}-1+2{\sqrt {{\sqrt {5}}-2}}}{8}}}\right).}
大二重扭稜二重斜方十二面體頂點圖 的視覺化呈現。 頂點圖 為頂角結構的一種描述方式,通常是以構成頂角之多面角組成面的邊數順序來表示。一般而言會將大二重扭稜二重斜方十二面體的頂點圖計為(5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2 ,以表示每個頂角皆為12面角,並依照五角星(5/2)、正方形(4)、三個三角形(3.3.3 )、正方形(4)、反向相接的五角星(5/3 )、正方形(4)、三個反向相接的三角形(3/2.3/2.3/2 )、正方形(4)的順序相接,並圍繞頂角兩圈(/2 )[ 4] :122 。然而考慮部分邊的重合性,可以將的頂角分成兩組,其頂點圖分別為[5/4,4,3,3,3,4,5/3,4,3/2,3/2,3/2,4] 與[5/2,3,4,3,4,3,5/3,3/2,4,3/2,4,3/2] 。[ 1]
若將重合邊視為相異,則大二重扭稜二重斜方十二面體由204個面、360條邊和60個頂點組成,其邊數為360[ 13] 歐拉示性數 為
χ
=
F
−
E
+
V
=
{\displaystyle \chi =F-E+V=}
204
−
360
+
60
=
−
96
{\displaystyle {{{204}-{360}}+{60}}=-96}
歐拉示性數 為
χ
=
F
−
E
+
V
=
{\displaystyle \chi =F-E+V=}
204
−
240
+
60
=
24
{\displaystyle {{{204}-{240}}+{60}}=24}
[ 4]
大二重扭稜二重斜方十二面體與大二重斜方截半二十面體 共用相同的邊佈局 [ 14] 二十複合正八面體 [ 1] 四面半六面體 [ 16] 二十複合四面半六面體 大扭稜十二面截半二十面體
^ 1.0 1.1 1.2 1.3 1.4 Richard Klitzing. gidisdrid . bendwavy.org. [2022-07-10 ] . (原始内容存档 于2022-07-13). ^ Coxeter, Harold Scott MacDonald ; Longuet-Higgins, M. S.; Miller, J. C. P. Uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society). 1954, 246 (916): 401–450. ISSN 0080-4614 JSTOR 91532 MR 0062446 S2CID 202575183 doi:10.1098/rsta.1954.0003 ^ Sopov, S. P., A proof of the completeness on the list of elementary homogeneous polyhedra, Ukrainskiui Geometricheskiui Sbornik, 1970, (8): 139–156, MR 0326550 ^ 4.0 4.1 4.2 4.3 4.4 4.5 Skilling, J., The complete set of uniform polyhedra, Philosophical Transactions of the Royal Society of London. Series A 278 : 111–135, ISSN 0080-4614 JSTOR 74475 MR 0365333 doi:10.1098/rsta.1975.0022 ^ Jim McNeill. Skilling's Figure . orchidpalms.com. [2022-07-10 ] . (原始内容存档 于2022-07-12). ^ Azulay, J. and Rice, B. and Aiello, C. Architecture Xenoculture . eVolo. eVolo Press. 2014 [2021-10-28 ] . ISBN 9781938740121存档 于2021-10-29). ^ Robert Webb. Great Dirhombicosidodecahedron ("Miller's Monster") . software3d.com. [2021-10-25 ] . (原始内容存档 于2022-03-05). ^ Verheyen, Hugo F. The complete set of Jitterbug transformers and the analysis of their motion. Symmetry 2 (Elsevier). 1989: 203–250. ^ Elwes, R. and Elwes, R. Maths 1001: Absolutely Everything That Matters in Mathematics . Quercus. 2017 [2022-07-10 ] . ISBN 9781786486950存档 于2022-07-13). ^ Kasparian, Raffi J and Petillo, Alice E. Introducing the Kasparian Constructions. Proceedings of Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture. 2017: 511––514. ^ 11.0 11.1 George W. Hart. The Great Disnub Dirhombidodecahedron . Virtual Polyhedra. 1996 [2022-07-10 ] . (原始内容存档 于2022-07-14). ^ Kay West. The Mathematics Tarot Handbook. ^ 13.0 13.1 Kay West[ 12]
^ 14.0 14.1 Richard Klitzing. gidrid . bendwavy.org. [2022-07-10 ] . (原始内容存档 于2022-07-13). ^ Data of Great Dirhombicosidodecahedron . dmccooey.com. [2021-10-28 ] . (原始内容存档 于2016-05-30). ^ Tetrahemihexahedron . software3d.com. [2021-07-29 ] . (原始内容存档 于2021-07-29).