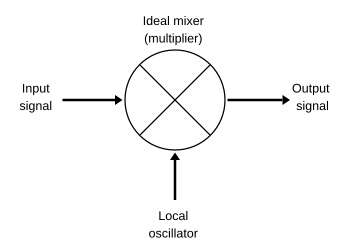
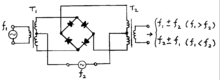
在电子学中，混频器是一种非線性电路，它可以由施加到它的两个信号产生新的频率。其最常见的应用是频率分别为 f₁ 和 f₂ 的两个信号加在一个混频器上，产生原来两频率的和 f₁ + f₂ 与差 f₁ - f₂ 的新信号，称作外差。实际混频器还有可能产生其他频率分量。

混频器广泛用于将信号从一个频率范围搬移到另一个，此过程称作外差作用，以便于传输或进一步的信号处理。例如，超外差收音机的一个关键部件是一个用来搬移接收到的信号到一个共同的中频。混频器也用于在无线电发射机中調變载波。

混频器的本质特性是它在输出信号中产生一个两路输入信号的乘积的分量。具有非线性（如指数）特性的器件可以用作混频器。无源混频器使用一个或多个二极管，并依赖于其电压和电流之间的非线性关系，以实现乘法计算。在无源混频器中，得到的输出信号的功率总是比输入信号低。

有源混频器使用放大器件（如晶体管或真空管）来增加输出信号的强度。有源混频器提高了端口之间的隔离度，但可能会增大噪声和功耗。有源混频器对过载的耐受性较差。

混频器可以做成分立元件，也可以是集成电路的一部分，也可以作为混合模块提供。

混频器也可按其拓扑分类：

• 非平衡混频器，产生乘积信号的同时会允许两个输入信号通过并作为输出的成分存在。
• 单平衡混频器会将其中一个输入加到平衡（差分）电路中，以使本地振荡（LO）或信号输入（RF）施加在输入上，但并不是两个输入都有。
• 双平衡混频器将两个输入都加在了差分电路中，于是两个输入信号都不会出现，只有乘积信号会出现在输出中。^[1] 双平衡混频器相对于非平衡与单平衡混频器更加复杂，驱动电平也更高。

对一个特定应用来说选取混频器的类型是一个权衡的过程。

混频器电路具有变频增益（或损耗）和噪声系数（英语：noise figure）等特性。^[2]

用作混频器的非线性电子元件包括二極管、晶体管近截止偏置，在低频下有模拟乘法器。充到饱和的磁芯电感也被使用。在非线性光学中，具有非线性特性的晶体用于混合两种频率的激光用于产生光外差（英语：Optical heterodyne detection）。

二極管可以用来制作简单的不平衡混频器。这种类型的混频器产生的信号会包含原始频率以及它们的和与差。二极管的显着特性是它的非线性（或非欧姆行为），这意味着它的响应（电流）不与其输入（电压）成正比。因此二极管不会再生流过它的电流的驱动电压的频率，这就可以控制所需频率。 通过理想二极管的电流 I 作为电压 V 的函数为

${\displaystyle I=I_{\mathrm {S} }\left(e^{qV_{\mathrm {D} } \over nkT}-1\right)}$

其中 V 以 e 指数出现是很重要的。指数函数的泰勒级数为

${\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}}$

对于较小的 x（即电压较小）可以通过这个级数的前几项来估计：

${\displaystyle e^{x}-1\approx x+{\frac {x^{2}}{2}}}$

假设两个输入信号之和 ${\displaystyle v_{1}+v_{2}}$ 加在一个二极管上，产生的输出电压与流过二极管（可能是通过提供加在与二极管串联的電阻器两端的电压）成正比。然后，忽略二极管方程中的常量，输出电压的形式就会为

${\displaystyle v_{\mathrm {o} }=(v_{1}+v_{2})+{\frac {1}{2}}(v_{1}+v_{2})^{2}+\dots }$

正如预期的那样，右边的第一项是原始的两个信号，接着是二者之和的平方，写作 ${\displaystyle (v_{1}+v_{2})^{2}=v_{1}^{2}+2v_{1}v_{2}+v_{2}^{2}}$，其中乘积信号是很明显的。省略号表示所有二者和的更高次幂，对于小信号来说我们认为可以忽略。

假设两个不同频率的正弦输入信号输入到该二极管，使得 ${\displaystyle v_{1}=\sin at}$，${\displaystyle v_{2}=\sin bt}$。信号 ${\displaystyle V_{0}}$ 就会为：

${\displaystyle v_{\mathrm {o} }=(\sin at+\sin bt)+{\frac {1}{2}}(\sin at+\sin bt)^{2}+\dots }$

展开平方项就会得到：

${\displaystyle v_{\mathrm {o} }=(\sin at+\sin bt)+{\frac {1}{2}}(\sin ^{2}at+2\sin at\sin bt+\sin ^{2}bt)+\dots }$

将除了 ${\displaystyle \sin at\sin bt}$ 之外的项都忽略并运用积化和差恒等式

${\displaystyle \sin a\sin b={\frac {\cos(a-b)-\cos(a+b)}{2}}}$

得到，

${\displaystyle v_{\mathrm {o} }=\cos((a-b)t)-\cos((a+b)t)+\dots }$

说明了混频器是如何产生新频率的。