在粒子物理學 中,量子電動力學 (quantum electrodynamics ,簡稱QED 電動力學 的相對論 性量子場論 。它在本質上描述了光 與物質 間的相互作用 ,而且它還是第一套同時完全符合量子力學 及狹義相對論 的理論。量子電動力學在數學上描述了所有由帶電荷 粒子經交換光子 產生的相互作用所引起的現象 ,同時亦代表了古典電動力學 所對應的量子 理論,為物質與光的相互作用提供了完整的科學論述。
用術語來說,量子電動力學就是電磁量子真空態 的微擾理論 。它的其中一個創始人,理查德·費曼 把它譽為「物理學的瑰寶」("the jewel of physics") ,原因是它能為相關的物理量提供極度精確的預測值 異常磁矩 及氫 原子能階 的蘭姆位移 [ 1] :Ch1 。
保羅·狄拉克 輻射與物質間相互作用的第一套量子理論 ,是由英國物理學家保羅·狄拉克 提出的,他在1920年代就成功計算出原子 的自發發射係數[ 2]
狄拉克用一整組的諧振子,加上新開發的粒子創生及消滅算符 ,成功地描述了電磁場 的量子化。在之後的幾年,沃爾夫岡·泡利 、尤金·維格納 、帕斯庫爾·約當 、維爾納·海森堡 都在這方面作出了貢獻,還有恩里科·費米 更提出了一套優雅的量子電動力學表述[ 3] 費利克斯·布洛赫 和阿諾德·諾德西克 [ 4] 維克托·魏斯科普夫 [ 5] 微擾理論 上獲得可靠結果,而這個問題羅伯特·奧本海默 早在1930年已經指出了[ 6] 狹義相對論 與量子理論 在基礎上並不相容。
漢斯·貝特 這套理論的難度在四十年代末期繼續提昇。微波 科技的進步,使得物理學家能夠更準確地測量出氫 原子的能階轉移[ 7] 蘭姆位移 及電子磁矩 [ 8]
突破的可能點由漢斯·貝特 於1940年代末率先提出。1947年,他在設爾特島 研討會上講完有關能階位移的講座之後,就從紐約 乘火車到斯克内克塔迪 ,期間他成功完成了第一份氫原子線位移的非相對論性計算,這種位移是由威利斯·蘭姆 與羅伯特·雷瑟福 [ 9] 質量 和電荷 被定為一個有限值,而這個計算的獨創性就在於,直接把無限置於質量和電荷的修正值中。這樣做的話,無限就會被這些常數所吸收,從而得出與實驗相符的有限值。這個步驟叫重整化 。
理查德·費曼 (中)與羅伯特·奧本海默 (右),攝於洛斯阿拉莫斯國家實驗室 。基於貝特的直覺,朝永振一郎 [ 10] 朱利安·施溫格 [ 11] [ 12] 理查德·費曼 [ 13] [ 14] [ 15] 弗里曼·戴森 [ 16] [ 17] 協變 的表述,終於使任意階的量子電動力學微擾數列變得有限。因這方面的貢獻,朝永振一郎 、朱利安·施溫格 與理查德·費曼 共同獲得了1965年的諾貝爾物理學獎 [ 18] 弗里曼·戴森 的,是關於量子電動力學的協變 與規範不變 表述,這種表述使得物理學家們可以在任意階的微擾數列中計算出可觀測量。費曼的數學技巧,是基於他本人所創的圖 ,看起來好像跟施溫格與朝永的解題方法非常不同,他們用的是基於場論及算符的方法。但後來弗里曼·戴森證明了這兩套方法其實是相同的[ 16] 積分 ,為理論中的某些發散賦予物理意義,這個需要就是重整化 ,它成為了量子場論的一項基礎,後來更成為一套理論是否能被認受的準則。儘管計算上重整化的效用是出奇地好,費曼從來都沒有對它的數學有效性有十足的信心,他甚至把重整化叫做“騙局”及“花招”[ 1] :128 。
時至今日,量子電動力學已經成了後來所有量子場論的模範與模板。其中一個後續理論就是量子色動力學 ,它的研究從1960年代開始,在休·波利策 、西德尼·科爾曼 、戴維·格婁斯 與弗朗克·韋爾切克 的貢獻下,於1975年達至現在的形態。謝爾登·格拉肖 、史蒂文·溫伯格 與阿卜杜勒·薩拉姆 各自獨立地證明了弱核力 與量子電動力學,是可以統一成單一的一種電弱力 ,而這項研究是基於多位物理學家的前瞻性貢獻,其中包括朱利安·施溫格 、傑拉德·古拉尼 、卡爾·哈庚 和湯姆·基博爾 [ 19] [ 20] 彼得·希格斯 、傑弗里·戈德斯通 等。
費曼在臨終前的幾年,為了未受過科學訓練的群眾,主講了一系列有關量子電動力學的講座。這些講座被抄錄下來,並結集成書,於1985年出版,書名為《QED:光和物質的奇異性 》[ 1]
費曼對量子電動力學的說明中,有一項關鍵,那就是三個基本作用[ 1] :85 :
一光子 從一時間地點,移動到另一時間地點
一電子 從一時間地點,移動到另一時間地點
一電子在某一時間地點,發射或吸收一光子 費曼圖 的元素這些作用可以用圖像表示,也就是費曼圖 的三種基本元素:波浪線代表光子,直線代表電子,兩直線與一波浪線的交匯處代表電子發射或吸收光子的頂點 。見右圖。
重點是,不要過度詮釋這些圖。不要從這些圖中引申出粒子是如何從一點移動到另一點的。這些圖並沒有代表着粒子會以直線或曲線移動。它們也不代表粒子會以固定速度行進。按慣例使用波浪線代表光子的這件事,並不意味着認定光子比電子更像波。這些圖只是單純代表上述作用的符號:光子和電子確實會以某種方式從一點移動到另一點,而電子也確實會以某種方式發射及吸收光子。實際上人們尚未能了解這些事是如何發生的,但是理論會計算出這些事發生的機率。
費曼除了介紹了這些作用的圖像表示之外,還為一個數量提供了另一種表示方式,這個數量叫機率幅 。機率幅的平方就是機率。假設一光子由一時間空間(標記為A)移動到另一時間空間(標記為B),那麼費曼就會用
P
(
A
→
B
)
{\displaystyle P(A\rightarrow B)}
E
(
C
→
D
)
{\displaystyle E(C\rightarrow D)}
j
{\displaystyle j}
電荷
e
{\displaystyle e}
[ 1] :91 。
量子電動力學是基於一個假設的,就是假設所有多個電子與光子間的複雜相互作用,都能夠以適當地組合上述三種構成要素來代表,然後以機率幅計算出這些複雜相互作用的機率。原來只需要假設前面提到的機率幅(
P
(
A
→
B
)
{\displaystyle P(A\rightarrow B)}
E
(
C
→
D
)
{\displaystyle E(C\rightarrow D)}
j
{\displaystyle j}
下文所用的機率幅有着以下的基本規則[ 1] :93 :
若一事件能以多種不同的方式發生,那麼其機率幅為各發生方式機率幅的和;
若一過程中包括多種獨立的子過程,則其機率幅為各子過程機率幅的積。
假設開始時在某時間和空間處(這時間和空間的標記為A)有一電子,在另一時間和空間處(標記為B)有一光子。從物理學的觀點,一條典型的問題會問「在C(另一時間和空間)處出現電子,而在D(又另一時間和空間)處出現光子的機率是多少?」要做到這一點,最簡單的過程就是讓電子從A移動到C(一種基本作用),讓光子從B移動到D(另一種基本作用)。已知兩個子過程的機率幅——
P
(
A
→
B
)
{\displaystyle P(A\rightarrow B)}
E
(
C
→
D
)
{\displaystyle E(C\rightarrow D)}
康普頓散射 但是還有其他可以得出相同終點的其他過程。電子可以在時間和空間E處把光子吸收掉,然後移動至F處時發射出另一光子,最終電子移動到C處時被探測到,而新的光子則移動到D處。這個複雜過程的機率幅還是可以經由各分作用的機率幅得知:當中共有三個電子作用、兩個光子作用及兩個頂點——其中一個發射,一個吸收。將各個機率幅相乘,可得任何已定的E及F處的總機率幅。然後按規則一,將所有不同E及F處的總機率幅相加起來(實際上這加法並不基本,需要使用積分 法)。但是還有另一種可能性,就是電子首先移動到G處,發射出前往D處的光子,而電子則繼續移動到H處,並在該處吸收掉開始時的光子,最終移動到C處。同樣地,可以計算出這些可能性(全部的G及H)的機率幅。然後,把這兩種可能的機率幅,與開始時作的簡單估計相加,就可能得出一個更好的機率幅估計值。順便提一下,這種電子和光子的相互作用有一個名字,叫康普頓散射 [ 1] :97-98 。
中間過程的數量為無限,因為過程中能吸收及/或發射更多更多的光子。每一個可能性就有一張費曼圖。這意味着要計算出最終的機率幅,會是一項相當複雜的計算。然而,在量子電動力學中,愈複雜的費曼圖,對最終結果的貢獻也就愈小,因此要為原問題的答案計算出所需的準確度,只是時間與精力的問題[ 1] :96-97 。這就是解決量子電動力學的基本手法。要計算出任何光子與電子間的相互作用過程,首先用費曼圖列出所有可能的作用方式,而這些方式都是用那三種基本元素所組合而成的。在計算每一個圖的機率幅時,都要用到一些固定的規則。
當轉換成量子描述的時候,物理的基本框架依然不變,但是有些概念需要改變。其中一種就是,認為粒子的移動點是會受到一些限制的,就像日常生活一樣,但是在完整的量子電動力學下,情況並不是這樣的。在A處的電子或在B處的光子,在以基本作用移動時,是有可能到達宇宙任何時間點或空間點的。這包括需要超越光速才能到達的地方,及之前的時間點。(逆時間移動的電子可被視為順時間移動正電子 [ 1] :89, 98-99 。)
費曼把複數 換成旋轉的箭頭,這些箭頭從發射開始,到粒子被探測到時結束。這些箭頭的總和代表事件的總概率。在上圖中,由來源S所發射的光被鏡片(紫色水平線)反射後,到達位於點P探測器。必須考慮所有路徑的總和。上圖下方的圖表所描繪的是各路徑從P到S所需的時間。 量子力學 對機率的計算方式引入了一項重大的改變。機率仍然是以實數 表示,如同日常生活中常用的機率,然而量子力學的機率是由機率幅計算。而機率幅 是複數 。
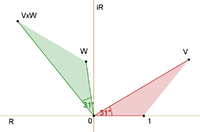
費曼為了避免讀者接觸到複數的數學,使用了一種簡單但準確的代表,就是用一張紙上或一塊屏幕上的箭頭代表複數。(請千萬不要把這些箭頭與費曼圖的箭頭混淆,後者實際上代表着三維空間與一維時間在簡化後所得的二維空間關係)這些幅箭頭對描述量子理論的世界非常重要。對於為甚麼需要這些箭頭,還沒有任何令人滿意的理由。但由於它們很實用,所以也只它們是所有量子現象描述中的重要組成部分。它們與日常熟知的機率間有一條簡單的規則,就是一事件的發生機率是其輻箭頭長度的平方。因此,若某過程含有兩個機率幅v 及w ,則該過程的發生機率為
P
=
|
v
+
w
|
2
{\displaystyle P=|\mathbf {v} +\mathbf {w} |^{2}}
或
P
=
|
v
×
w
|
2
.
{\displaystyle P=|\mathbf {v} \times \mathbf {w} |^{2}.}
至於要使用加號還是乘號,規則還是與上文提及的一樣。在你以為要加或乘機率的地方,此時要加或乘的卻是機率幅,是複數。
複數機率幅的加法 複數機率幅的乘法 在複數理論中,加法和乘法是為人所熟知的運算,可用左圖表示。加法的方法如下。把第二個箭頭的起端接到第一個箭頭末端,那麼其和就是第三個箭頭,由第一個箭頭的起端指向第二個箭頭的末端。兩個箭頭的積,就是一個長度為該兩個箭頭長度積的箭頭。把兩箭頭相對於一參考方向的轉動角度加起來,可得積箭頭的方向,也就是積箭頭相對於該參考方向的轉動角度。
把機率換成機率幅的這一轉變,把數學變得更複雜了,但是基本手法仍然不變。但只是那個轉變仍不是很足夠,因為忽略了電子及光子都可以被極化 這一點,也就是說必須考慮它們在時間和空間中的方向。因此
P
(
A
→
B
)
{\displaystyle P(A\rightarrow B)}
[ 1] :120-121 。物理量
j
{\displaystyle j}
與電子可被極化這一點相關的,還有另一樣必須的細節,就是電子是一種費米子 ,因此遵從費米-狄拉克統計 。基本規則就是,若某複雜過程中有超過一個電子時,在計算其機率幅時,會包括(這通常是必須的)互補的費曼圖,即圖中的兩個電子事件被交換了,這樣所得的機率幅與交換前的值一樣,但就會成了負值。最簡單的例子,就是以A、B作起點,C、D作終點的兩個電子。那麼機率幅則為兩個過程機率幅的「差」,即
E
(
A
→
D
)
×
E
(
B
→
C
)
−
E
(
A
→
C
)
×
E
(
b
→
D
)
,
{\displaystyle E(A\rightarrow D)\times E(B\rightarrow C)-E(A\rightarrow C)\times E(b\rightarrow D),}
但從日常的機率中,這個情況時一般是會用和的[ 1] :112-113 。
最後,必須計算出P(A→B)和E(C→D),這兩個量分別對應光子和電子的機率幅。它們實際上是狄拉克方程 與克萊因-戈爾登方程 的解,其中前者描述的是電子機率幅的變化,而後者描述的則是光子[ 21] :225-229 。這兩個量稱為費曼傳播子 。在一般文獻中的標記翻譯如下:
P
(
A
→
B
)
→
D
F
(
x
B
−
x
A
)
,
E
(
C
→
D
)
→
S
F
(
x
D
−
x
C
)
{\displaystyle P(A\rightarrow B)\rightarrow D_{F}(x_{B}-x_{A}),\quad E(C\rightarrow D)\rightarrow S_{F}(x_{D}-x_{C})}
其中類似
x
A
{\displaystyle x_{A}}
電子自身能量 迴圈在量子電動力學的發展史上,有一個難題使研究進度停滯了二十年:雖然在開始時假設只有三種基本的「簡單」作用,但遊戲規則上說,如果要計算一電子從A到B的機率幅,就必須考慮全部可能的方式:即所有起點為A終點為B的費曼圖。因此,電子可以移動到C,然後發射一光子,之後在移動到B之前在D再吸收之前的光子。又或是電子重覆上述行動兩次,或更多的次數。總而言之,這是一個類似分形 的情況,若仔細去看一條線時,看見它分解成一系列「簡單」的線,而這些線在細看之下,也會分解成一系列「簡單」的線,一直下去,永無止境。這是一個很難應付的情況。如果加入這些細節只是稍為帶來改變的話,那就還可以。但是後來發現在一些情況下,簡單的修正也不能解決上述導致無限機率幅,因此結果是災難性的。最後這個難題用一種叫重整化 的技巧「解決」。不過,費曼本人對此並不高興,把它叫做“一套沒頭沒腦的程序”[ 1] :128 。
在以上的框架下,物理學家當時就能夠高度準確地計算出電子的一些屬性,例如異常磁矩 。然而,就像費曼所指出的那樣,這套理論完全解釋不了為甚麼電子會有它們現有的這樣一個質量。費曼這樣表示,“沒有理論能夠充分地解釋這些數。我們所有的理論都用到這些數,但我們不明白這些數──它們是甚麼,又或是它們從哪裏來的。從一個基礎的視點出發,我相信這是一個有趣且須認真對待的難題。”[ 1] :152
數學上,量子電動力學有著阿貝爾群 規範理論 的結構,並有一對稱群——U(1) 規範群 。媒介帶電自旋-1/2 場 之間交互作用的規範場 是電磁場 。採用
c
=
ℏ
=
μ
0
=
1
{\displaystyle c=\hbar =\mu _{0}=1}
自然單位制 ,量子電動力學中透過光子 來媒介數個電子 或正子 間之交互作用的拉格朗日量 是[ 22] :78 [ 23] :224
L
=
ψ
¯
(
i
γ
μ
D
μ
−
m
)
ψ
−
1
4
F
μ
ν
F
μ
ν
{\displaystyle {\mathcal {L}}={\bar {\psi }}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }\,}
其中
γ
μ
{\displaystyle \gamma _{\mu }\,\!}
狄拉克矩陣 ,
ψ
{\displaystyle \psi }
自旋1/2 粒子(例如電子 -正電子 場)的雙旋量 場 ,
ψ
¯
≡
ψ
†
γ
0
{\displaystyle {\bar {\psi }}\equiv \psi ^{\dagger }\gamma ^{0}}
狄拉克伴旋量
D
μ
=
∂
μ
+
i
e
A
μ
{\displaystyle D_{\mu }=\partial _{\mu }+ieA_{\mu }\,\!}
規範 協變 導數 ,而
e
{\displaystyle \ e}
基本電荷 ),
A
μ
{\displaystyle \ A_{\mu }}
協變 電磁場 向量勢 ,
F
μ
ν
=
∂
μ
A
ν
−
∂
ν
A
μ
{\displaystyle F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\,\!}
電磁場張量 。
推導開始,首先將D 的定義代入拉格朗日量 ,得到L 為
L
=
i
ψ
¯
γ
μ
∂
μ
ψ
−
e
ψ
¯
γ
μ
A
μ
ψ
−
m
ψ
¯
ψ
−
1
4
F
μ
ν
F
μ
ν
(
1
)
{\displaystyle {\mathcal {L}}=i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma _{\mu }A^{\mu }\psi -m{\bar {\psi }}\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }\quad \quad \quad (1)\,}
再來將拉格朗日量代入針對代表帶電粒子場 的歐拉-拉格朗日方程式 [ 22] :16
∂
μ
(
∂
L
∂
(
∂
μ
ψ
)
)
−
∂
L
∂
ψ
=
0
(
2
)
{\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)-{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (2)\,}
以找出量子電動力學的場方程式。
源自此一拉格朗日量的兩項則分別為
∂
μ
(
∂
L
∂
(
∂
μ
ψ
)
)
=
∂
μ
(
i
ψ
¯
γ
μ
)
{\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)=\partial _{\mu }\left(i{\bar {\psi }}\gamma ^{\mu }\right)\,}
∂
L
∂
ψ
=
−
e
ψ
¯
γ
μ
A
μ
−
m
ψ
¯
{\displaystyle {\frac {\partial {\mathcal {L}}}{\partial \psi }}=-e{\bar {\psi }}\gamma _{\mu }A^{\mu }-m{\bar {\psi }}\,}
將此二項代回歐拉-拉格朗日方程式 (2) 得到
i
∂
μ
ψ
¯
γ
μ
+
e
ψ
¯
γ
μ
A
μ
+
m
ψ
¯
=
0
{\displaystyle i\partial _{\mu }{\bar {\psi }}\gamma ^{\mu }+e{\bar {\psi }}\gamma _{\mu }A^{\mu }+m{\bar {\psi }}=0\,}
以及複數共軛
i
γ
μ
∂
μ
ψ
−
e
γ
μ
A
μ
ψ
−
m
ψ
=
0
{\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi -e\gamma _{\mu }A^{\mu }\psi -m\psi =0\,}
若將後者的中間項移到等號右邊則得:
i
γ
μ
∂
μ
ψ
−
m
ψ
=
e
γ
μ
A
μ
ψ
{\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi -m\psi =e\gamma _{\mu }A^{\mu }\psi \,}
左手邊則形式與原本狄拉克方程式 相似,而右手邊則是與電磁場的交互作用。
另個更重要的方程式是將拉格朗日量代入另個歐拉-拉格朗日方程式,但這個方程式現在是針對
A
μ
{\displaystyle A^{\mu }}
∂
ν
(
∂
L
∂
(
∂
ν
A
μ
)
)
−
∂
L
∂
A
μ
=
0
(
3
)
{\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)-{\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (3)\,}
類似的兩項在此則為
∂
ν
(
∂
L
∂
(
∂
ν
A
μ
)
)
=
∂
ν
(
∂
μ
A
ν
−
∂
ν
A
μ
)
{\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)=\partial _{\nu }\left(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }\right)\,}
∂
L
∂
A
μ
=
−
e
ψ
¯
γ
μ
ψ
{\displaystyle {\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=-e{\bar {\psi }}\gamma ^{\mu }\psi \,}
而此二項代回到 (3) 可得[ 22] :78
∂
ν
F
ν
μ
=
e
ψ
¯
γ
μ
ψ
{\displaystyle \partial _{\nu }F^{\nu \mu }=e{\bar {\psi }}\gamma ^{\mu }\psi \,}
現在,如果讓四維勢 的散度 消失,即採用洛倫茨規範條件 :
∂
μ
A
μ
=
0
{\displaystyle \partial _{\mu }A^{\mu }=0}
則可得
◻
A
μ
=
e
ψ
¯
γ
μ
ψ
,
{\displaystyle \Box A^{\mu }=e{\bar {\psi }}\gamma ^{\mu }\psi \,,}
此為四維勢的波動方程式 ,洛倫茨規範條件下量子電動力學版本的古典麥克斯韋方程組 。(在上式中,正方形代表達朗貝爾算符 )
把玻色子 與費米子 部分視作自由,則理論的量子化並不複雜。這樣就可以構建一組漸近態,用於計算不同過程的機率幅。要做到這點,首先要計算出演進算符 ,這樣就能從已知起始態
|
i
⟩
{\displaystyle |i\rangle }
狄拉克符號 )得出
⟨
f
|
{\displaystyle \langle f|}
[ 22] :5
M
f
i
=
⟨
f
|
U
|
i
⟩
.
{\displaystyle M_{fi}=\langle f|U|i\rangle .}
這種技巧叫S矩陣 。演進算符是由相互作用繪景 所得,其中時間演進從哈密頓算符而來,即上述拉格朗日量第二項的空間積分,[ 22] :123
V
=
e
∫
d
3
x
ψ
¯
γ
μ
ψ
A
μ
{\displaystyle V=e\int d^{3}x{\bar {\psi }}\gamma ^{\mu }\psi A_{\mu }}
由此可得[ 22] :86
U
=
T
exp
[
−
i
ℏ
∫
t
0
t
d
t
′
V
(
t
′
)
]
{\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'V(t')\right]}
其中T為時間排序 算符,V(t')则是相互作用绘景中的相互作用算符。演進算符只在作為數列時具有意義,而此時所得的是以精細結構常數 為發展參數的微擾數列 。這種數列叫戴森數列
儘管費曼的量子電動力學研究法在概念上相當清晰,但是早期幾乎沒有教科書引用他的手法。在計算時,使用傳播子的傅里葉變換 會使計算簡便得多。量子物理考慮的是粒子的動量 ,而不是它們的位置。在相互作用中把粒子視作被創造或湮滅,也是一件方便的事。這樣費曼圖還是跟之前的一樣,但是對線的詮釋就不同了。電子線代表的是帶某能量與動量的電子,而對光子線的詮釋也是這樣。頂點圖所代表的是一電子的湮滅與另一電子的創造,同時還有一光子的吸收或創造,上述的三種粒子都有各自特定的能量與動量。
形式散射理论给出了散射截面 和S矩阵 乃至散射振幅的关系。依据LSZ约化公式 奇点 处的行为联系起来。再根据盖尔曼–劳定理 ,相互作用系统的编时传播子可以写成包含自由场算符、自由真空和相互作用绘景中时间演化算符的表达式。展开时间演化算符,再在戴森級數的項上使用威克定理 ,就可以将相互作用系统的编时传播子转化为自由场费曼传播子构成的级数。費曼圖 是一种计算这些级数项的技巧。在量子電動力學中,圖各部份對應的規則如下:[ 22] :801-802
除上述規則外,圖中有迴圈時還必須加上動量積分
∫
d
p
4
2
π
4
{\displaystyle \int {\frac {dp^{4}}{2\pi ^{4}}}}
虛粒子 )並不受任何特定的能量-動量所限——連一般在狹義相對論 中所需的都限制不了。由此按下面方式,要計算出機率幅 並不是一件複雜的事。下例為康普頓散射 ,即電子與光子間的彈性散射 [ 22] :158-159
由此可得S矩陣 一階微擾數列 中的對應機率幅
M
f
i
=
(
i
e
)
2
u
¯
(
p
→
′
,
s
′
)
ϵ
/
′
(
k
→
′
,
λ
′
)
∗
p
/
+
k
/
+
m
e
(
p
+
k
)
2
−
m
e
2
ϵ
/
(
k
→
,
λ
)
u
(
p
→
,
s
)
+
(
i
e
)
2
u
¯
(
p
→
′
,
s
′
)
ϵ
/
(
k
→
,
λ
)
p
/
−
k
/
′
+
m
e
(
p
−
k
′
)
2
−
m
e
2
ϵ
/
′
(
k
→
′
,
λ
′
)
∗
u
(
p
→
,
s
)
{\displaystyle M_{fi}=(ie)^{2}{\overline {u}}({\vec {p}}\,',s')\epsilon \!\!\!/\,'({\vec {k}}\,',\lambda ')^{*}{p\!\!\!/+k\!\!\!/+m_{e} \over (p+k)^{2}-m_{e}^{2}}\epsilon \!\!\!/({\vec {k}},\lambda )u({\vec {p}},s)+(ie)^{2}{\overline {u}}({\vec {p}}\,',s')\epsilon \!\!\!/({\vec {k}},\lambda ){p\!\!\!/-k\!\!\!/'+m_{e} \over (p-k')^{2}-m_{e}^{2}}\epsilon \!\!\!/\,'({\vec {k}}\,',\lambda ')^{*}u({\vec {p}},s)}
由此可計算出此散射的截面 。
計算演進算符的高階項不是一件複雜的事,不過這些項包含下面幾張簡單的圖:[ 22] :ch 10
對於
真空極化 函數
Π
{\displaystyle \Pi \,}
的
單圈(one-loop)貢獻
電子
自身能量 函數
Σ
{\displaystyle \Sigma \,}
的
單圈貢獻
頂點函數 (vertex function)
Γ
{\displaystyle \Gamma \,}
的
單圈貢獻
而這幾張圖都有密閉迴圈,意味着對應的積分 會紫外發散,计算电子自能和顶点函数时还会出现红外发散,因此在數學上沒有意義。為了克服這項困難,物理學家開發了一種叫重整化 的技巧,這樣做就會得到與實驗結果相符的有限數值。有一點很重要的是,理論在重整化後是否具有意義,是取決於其發散圖的數量是否無限。如果一理論的發散圖數量為有限的,那麼它就是可重整理論[ 22] :321 。這是因為要把觀測量重整,需要有限個的常數去維持預測值的不變。而量子電動力學正正是這樣的一套理論,而且它只有三個發散圖。重整化這個步驟所得的觀測量數值,與實驗所得的數值相差很少,例如電子的旋磁比 。
要成為一套切實可行的量子場論 ,具備可重整性是當中的一項重要準則。現時所有描述基本相互作用 的理論都是可重整理論,其中重力除外,它的量子部分仍是現時重要的熱門研究課題。
弗里曼·戴森 利用一則論述證明在量子電動力學裡微擾數列的收斂半徑 是零。[ 24] [ 25] 耦合常數 為負,庫侖力常數是負的,這等效於電磁作用力被反轉。此狀況下同電荷會相吸,異電荷會相斥,使得真空不穩定而自動衰變到一堆電子與正子,且電子與正子會自動分離於宇宙的不同角落。由於在負耦合常數下有此理論有問題,無論在耦合常數為零的點圈選多小的一個範圍,都會包含這些有問題的負耦合常數,因此數列的收斂半徑是零。量子電動力學的微擾數列不會收斂,只會是漸進級數。當計算更多項時,並不會改善其結果。這可以視為是微擾理論 的問題,需要一個新的理論來描述,或是直接計算而不管它。
^ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 Feynman, Richard . QED: The Strange Theory of Light and Matter. Princeton University Press. 1985. ISBN 978-0-691-12575-6 ^
P.A.M. Dirac . The Quantum Theory of the Emission and Absorption of Radiation. Proceedings of the Royal Society of London A. 1927, 114 (767): 243–265. Bibcode:1927RSPSA.114..243D doi:10.1098/rspa.1927.0039
^
E. Fermi . Quantum Theory of Radiation. Reviews of Modern Physics. 1932, 4 : 87–132. Bibcode:1932RvMP....4...87F doi:10.1103/RevModPhys.4.87
^ F. Bloch ; A. Nordsieck. Note on the Radiation Field of the Electron . Physical Review . 1937, 52 (2): 54–59. Bibcode:1937PhRv...52...54B doi:10.1103/PhysRev.52.54 ^ V. F. Weisskopf . On the Self-Energy and the Electromagnetic Field of the Electron . Physical Review. 1939, 56 : 72–85. Bibcode:1939PhRv...56...72W doi:10.1103/PhysRev.56.72 ^ R. Oppenheimer . Note on the Theory of the Interaction of Field and Matter . Physical Review. 1930, 35 (5): 461–477. Bibcode:1930PhRv...35..461O doi:10.1103/PhysRev.35.461 ^
W. E. Lamb ; R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method, . Physical Review. 1947, 72 (3): 241–243. Bibcode:1947PhRv...72..241L doi:10.1103/PhysRev.72.241
^
P. Kusch ; H. M. Foley. On the Intrinsic Moment of the Electron. Physical Review. 1948, 73 (3): 412. Bibcode:1948PhRv...73..412F doi:10.1103/PhysRev.73.412
^
H. Bethe . The Electromagnetic Shift of Energy Levels . Physical Review. 1947, 72 (4): 339–341. Bibcode:1947PhRv...72..339B doi:10.1103/PhysRev.72.339
^
S. Tomonaga . On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. Progress of Theoretical Physics. 1946, 1 (2): 27–42. doi:10.1143/PTP.1.27
^
J. Schwinger . On Quantum-Electrodynamics and the Magnetic Moment of the Electron . Physical Review. 1948, 73 (4): 416–417. Bibcode:1948PhRv...73..416S doi:10.1103/PhysRev.73.416
^
J. Schwinger . Quantum Electrodynamics. I. A Covariant Formulation . Physical Review . 1948, 74 (10): 1439–1461. Bibcode:1948PhRv...74.1439S doi:10.1103/PhysRev.74.1439
^
R. P. Feynman . Space–Time Approach to Quantum Electrodynamics . Physical Review . 1949, 76 (6): 769–789. Bibcode:1949PhRv...76..769F doi:10.1103/PhysRev.76.769
^
R. P. Feynman . The Theory of Positrons . Physical Review . 1949, 76 (6): 749–759. Bibcode:1949PhRv...76..749F doi:10.1103/PhysRev.76.749
^
R. P. Feynman . Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction . Physical Review . 1950, 80 (3): 440–457. Bibcode:1950PhRv...80..440F doi:10.1103/PhysRev.80.440
^ 16.0 16.1
F. Dyson . The Radiation Theories of Tomonaga, Schwinger, and Feynman . Physical Review . 1949, 75 (3): 486–502. Bibcode:1949PhRv...75..486D doi:10.1103/PhysRev.75.486
^
F. Dyson . The S Matrix in Quantum Electrodynamics . Physical Review . 1949, 75 (11): 1736–1755. Bibcode:1949PhRv...75.1736D doi:10.1103/PhysRev.75.1736
^ The Nobel Prize in Physics 1965 . Nobel Foundation. [2008-10-09 ] . (原始内容存档 于2018-12-26). ^
G.S. Guralnik, C.R. Hagen, T.W.B. Kibble. Global Conservation Laws and Massless Particles. Physical Review Letters . 1964, 13 (20): 585–587. Bibcode:1964PhRvL..13..585G doi:10.1103/PhysRevLett.13.585
^
G.S. Guralnik. The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles. International Journal of Modern Physics A. 2009, 24 (14): 2601–2627. Bibcode:2009IJMPA..24.2601G arXiv:0907.3466 doi:10.1142/S0217751X09045431
^ Griffiths, David J., Introduction to Elementary Particles 2nd revised, WILEY-VCH, 2008, ISBN 978-3-527-40601-2 ^ 22.00 22.01 22.02 22.03 22.04 22.05 22.06 22.07 22.08 22.09 Peskin, Michael; Schroeder, Daniel. An introduction to quantum field theory Reprint. Westview Press. 1995. ISBN 978-0201503975 ^ Schwarz, Matthew D. Quantum Field Theory and Standard Model. Cambridge University Press. 2014. ISBN 978-1-107-034730 ^ Dyson, Freeman , Divergence of Perturbation Theory in Quantum Electrodynamics, Physical Review 85 , 1951, 85 : 631–632 ^ Kinoshita, Toichiro. Quantum Electrodynamics has Zero Radius of Convergence Summarized from Toichiro Kinoshita . [2010-06-10 ] . (原始内容存档 于2021-04-28).
De Broglie, Louis . Recherches sur la theorie des quanta [Research on quantum theory]. France: Wiley-Interscience. 1925. Feynman, Richard Phillips . Quantum Electrodynamics New. Westview Press. 1998. ISBN 978-0-201-36075-2 Jauch, J.M.; Rohrlich, F. The Theory of Photons and Electrons. Springer-Verlag. 1980. ISBN 978-0-387-07295-1 Greiner, Walter; Bromley, D.A.; Müller, Berndt. Gauge Theory of Weak Interactions. Springer. 2000. ISBN 978-3-540-67672-0 Kane, Gordon, L. Modern Elementary Particle Physics . Westview Press. 1993. ISBN 978-0-201-62460-1 Miller, Arthur I. Early Quantum Electrodynamics: A Sourcebook . Cambridge University Press. 1995. ISBN 978-0-521-56891-3 Milonni, Peter W., (1994) The quantum vacuum - an introduction to quantum electrodynamics . Academic Press. ISBN 978-0-12-498080-8
Schweber, Silvan S. QED and the Men Who Made It . Princeton University Press. 1994. ISBN 978-0-691-03327-3 Schwinger, Julian . Selected Papers on Quantum Electrodynamics. Dover Publications. 1958. ISBN 978-0-486-60444-2 Tannoudji-Cohen, Claude ; Dupont-Roc, Jacques; Grynberg, Gilbert. Photons and Atoms: Introduction to Quantum Electrodynamics. Wiley-Interscience. 1997. ISBN 978-0-471-18433-1
Dudley, J.M.; Kwan, A.M. Richard Feynman's popular lectures on quantum electrodynamics: The 1979 Robb Lectures at Auckland University. American Journal of Physics. 1996, 64 (6): 694–698. Bibcode:1996AmJPh..64..694D doi:10.1119/1.18234








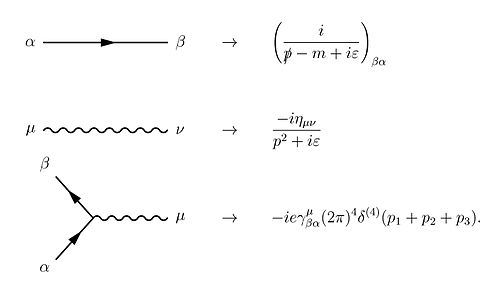






































![{\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'V(t')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6e8e9f54c6af1da0a81554513dab4bb8ba02f18)







