|
高级加密标准
進階加密标准(英語:Advanced Encryption Standard,缩写:AES),又称Rijndael加密法(荷兰语发音:[ˈrɛindaːl],音似英文的「Rhine doll」),是美国联邦政府采用的一種區塊加密标准。这个标准用来替代原先的DES,已經被多方分析且廣為全世界所使用。經過五年的甄選流程,進階加密標準由美國國家標準與技術研究院(NIST)於2001年11月26日發佈於FIPS PUB 197,並在2002年5月26日成為有效的標準。現在,進階加密标准已然成為对称密钥加密中最流行的演算法之一。 该演算法為比利时密码学家Joan Daemen和Vincent Rijmen所設計,結合兩位作者的名字,以Rijndael為名投稿進階加密標準的甄選流程。 沿革Rijndael是由Daemen和Rijmen早期所设计的Square改良而來;而Square則是由SHARK发展而来。 不同於它的前任標準DES,Rijndael使用的是代换-置换网络,而非Feistel架構。 密码说明严格地说,AES和Rijndael加密法並不完全一樣(虽然在实际应用中兩者可以互换),因为Rijndael加密法可以支援更大範圍的區塊和密钥长度:AES的區塊長度固定為128位元,密钥长度則可以是128,192或256位元;而Rijndael使用的密钥和區塊长度均可以是128,192或256位元。加密過程中使用的密钥是由Rijndael密钥生成方案產生。 大多数AES计算是在一个特别的有限域完成的。 AES加密過程是在一個4×4的位元組矩陣上運作,這個矩陣又称为「体(state)」,其初值就是一個明文區塊(矩陣中一個元素大小就是明文區塊中的一個Byte)。(Rijndael加密法因支援更大的區塊,其矩陣的「列數(Row number)」可視情況增加)加密时,各轮AES加密迴圈(除最后一轮外)均包含4个步骤:
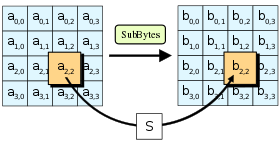
AddRoundKey步骤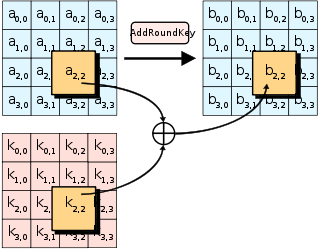 AddRoundKey步驟,回合金鑰將會與原矩陣合併。在每次的加密迴圈中,都會由主密鑰產生一把回合金鑰(透過Rijndael密鑰生成方案產生),這把金鑰大小會跟原矩陣一樣,以與原矩陣中每個對應的位元組作异或(⊕)加法。 SubBytes步骤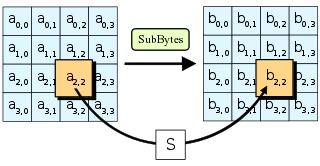 在SubBytes步骤中,矩陣中的各字節透過一個8位元的S-box進行轉換。這個步驟提供了加密法非線性的變換能力。S-box與上的乘法反元素有關,已知具有良好的非線性特性。為了避免簡單代數性質的攻擊,S-box結合了乘法反元素及一個可逆的仿射變換矩陣建構而成。此外在建構S-box時,刻意避開了不動點與反不動點,即以S-box替換字節的結果會相當於錯排的結果。Rijndael S-box條目有針對S-box的詳細描述。 ShiftRows步骤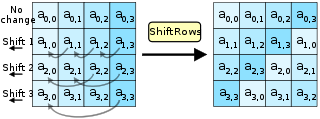 ShiftRows描述矩陣的行操作。在此步驟中,每一行都向左循環位移某個偏移量。在AES中(區塊大小128位元),第一行維持不變,第二行裡的每個位元組都向左循環移動一格。同理,第三行及第四行向左循環位移的偏移量就分別是2和3。128位元和192位元的區塊在此步驟的循環位移的模式相同。經過ShiftRows之後,矩陣中每一竖列,都是由輸入矩陣中的每個不同列中的元素組成。Rijndael演算法的版本中,偏移量和AES有少許不同;對於長度256位元的區塊,第一行仍然維持不變,第二行、第三行、第四行的偏移量分別是1位元組、2位元組、3位元組。除此之外,ShiftRows操作步驟在Rijndael和AES中完全相同。 MixColumns步骤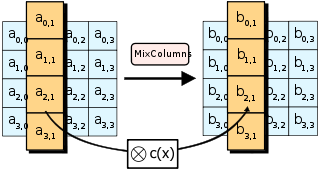 在MixColumns步骤,每一列的四個位元組透過线性变换互相結合。每一列的四個元素分別當作的係數,合併即為中的一個多項式,接著將此多項式和一個固定的多項式在模下相乘。此步驟亦可視為Rijndael有限域之下的矩陣乘法。MixColumns函数接受4個位元組的輸入,輸出4個位元組,每一個輸入的位元組都會對輸出的四個位元組造成影響。因此ShiftRows和MixColumns兩步驟為這個密碼系統提供了擴散性。 以下條目有對MixColumns更加詳細的描述:Rijndael mix columns 加密演算法优化使用32或更多位元定址的系統,可以事先對所有可能的輸入建立對應表,利用查表來實作SubBytes,ShiftRows和MixColumns步驟以達到加速的效果。這麼作需要產生4個表,每個表都有256個格子,一個格子記載32位元的輸出;約佔去4KB(4096位元組)記憶體空間,即每個表佔去1KB的記憶體空間。如此一來,在每個加密迴圈中,只需要查16次表,作12次32位元的XOR運算,以及AddRoundKey步驟中4次32位元XOR運算。若使用的平台記憶體空間不足4KB,也可以利用循環交換的方式一次查一個256格32位元的表。 然而,實際實作中應避免使用這樣的對應表,否則可能因為產生快取命中與否的差別而使旁道攻擊成為可能。 安全性截至2006年,针对AES唯一的成功攻击是旁道攻击或社會工程學攻擊。美国国家安全局审核了所有的參與競選AES的最終入圍者(包括Rijndael),认为他們均能夠满足美国政府傳遞非機密文件的安全需要。2003年6月,美国政府宣布AES可以用于加密机密文件:
(譯:AES加密演算法(使用128,192,和256位元密鑰的版本)的安全性,在設計結構及密鑰的長度上俱已到達保護機密資訊的標準。最高機密資訊的傳遞,則至少需要192或256位元的密鑰長度。用以傳遞國家安全資訊的AES實作產品,必須先由國家安全局審核認證,方能被發放使用。) 这标志着,由美国国家安全局NSA批准在最高机密資訊上使用的加密系統首次可以被公開使用。许多大众化产品只使用128位元密鑰當作預設值;由於最高機密文件的加密系統必須保證數十年以上的安全性,故推測NSA可能認為128位元太短,才以更長的密鑰長度為最高機密的加密保留了安全空間。 通常破解一個區塊加密系統最常見的方式,是先對其較弱版本(加密迴圈次數較少)嘗試各種攻擊。AES中128位元密鑰版本有10個加密迴圈,192位元密鑰版本有12個加密迴圈,256位元密鑰版本則有14個加密迴圈。至2006年為止,最著名的攻擊是針對AES 7次加密迴圈的128位元密鑰版本,8次加密迴圈的192位元密鑰版本,和9次加密迴圈的256位元密鑰版本所作的攻擊。[2] 由於已遭破解的弱版的AES,其加密迴圈數和原本的加密迴圈數相差無幾,有些密碼學家開始擔心AES的安全性:要是有人能將該著名的攻擊加以改進,這個區塊加密系統就會被破解。在密碼學的意義上,只要存在一個方法,比窮舉法還要更有效率,就能被視為一種「破解」。故一個針對AES 128位元密鑰的攻擊若「只」需要2120計算複雜度(少於窮舉法2128),128位元密鑰的AES就算被破解了;即便該方法在目前還不實用。從應用的角度來看,這種程度的破解依然太不切實際。最著名的暴力攻擊法是distributed.net針對64位元密鑰RC5所作的攻擊。 其他的爭議則著重於AES的數學結構。不像其他區塊加密系統,AES具有相當井然有序的代數結構。[3]雖然相關的代數攻擊尚未出現,但有許多學者認為,把安全性建立於未經透徹研究過的結構上是有風險的。Ferguson,Schroeppel和Whiting因此寫道:「...我們很擔心Rijndael演算法應用在機密系統上的安全性。」[4] 2002年,Nicolas Courtois和Josef Pieprzyk發表名為XSL攻擊的理論性攻擊,試圖展示AES一個潛在的弱點。但該攻擊的數學分析有點問題,推測應是作者的計算有誤。因此,這種攻擊法是否對AES奏效,仍是未解之謎。就現階段而言,XSL攻擊AES的效果不十分顯著,故將之應用於實際情況的可能性並不高。 旁道攻击旁道攻击,又称旁路攻击、侧信道攻击,是一种基于从密码系统的物理实现中获取的信息的攻击方式。它不攻击加密算法本身,而是攻击那些基於不安全系統(會在不經意間洩漏資訊)上的加密系統。 2005年4月,D.J. Bernstein公佈了一种缓存时序攻击法,他以此破解了一个装载OpenSSL AES加密系統的客戶伺服器[5]。為了設計使該伺服器公佈所有的時序資訊,攻击算法使用了2亿多条筛选过的明码。对于需要多个跳跃的国际互联网而言,这样的攻击方法并不实用[6]。Bruce Schneier稱此攻擊為「好的時序攻擊法」[7]。 2005年10月,Eran Tromer (页面存档备份,存于互联网档案馆)和另外兩個研究員發表了一篇論文,展示了數種針對AES的緩存時序攻擊法[8]。 注释参考文献引用
书目
外部链接
实现
参见 |
||||||||||||||||||||||||||