|
光學渦旋
光學渦旋(optical vortex)也稱為光渦,是光學場中的零點,也就是光強度為零的點。自從約翰·奈和迈克尔·贝里在1974年提出全面性的論文後,就開始了許多光學渦旋性質的研究[1],論文描述「光波列位錯」的基本性質,這個研究後來成為「奇點光學」(singular optics)的核心理論。 解釋在光學渦旋中,光會像螺旋開瓶器一般,沿著其軸扭轉。因為其扭轉,在軸的位置光會彼此相消。若投影在一平坦表面上,光學渦旋看起來會像一個光環,在中間有一個沒有光的黑色區域。這種螺旋形行進,中間黑暗的光,稱為光學渦旋。 光學渦旋的拓扑荷定義為其在一個波長的扭轉次數,拓扑荷恆為整數,依其扭轉方向可能是正數或是負數。拓扑荷越大表示光沿著軸旋轉的越快。此自旋會隨著光波列而有角動量,若有電偶極矩則會產生力矩。 光的軌道角動量可以由捕獲粒子的軌道運動來觀察。光學渦旋和平面光的干涉會出現同心螺旋的螺旋相位。 在實驗室中有許多方式可以產生光學渦旋。一般可以直接用雷射產生[2],或者用一些方式,將雷射光束變成渦旋,例如用電腦產生全息圖,螺旋相位延遲的結構,或是材料中的雙折射渦旋。 性質光學奇點是光場中的零點。在場中的相位會沿著零強度的點旋轉(因此稱為渦旋)。光學渦旋在二維場中為一個點,在三維場中為一條線(其余維數為2)。將場中的相位沿著包圍渦流的路徑場積分,會得到2π的整數倍。此整數稱為光學渦旋的拓扑荷或是強度。 超几何高斯光束(HyGG)在其中心有一個光學渦旋,光束的形式為 為旁軸波動方程含有贝塞尔函数的解(參照近軸近似)。超几何高斯光束中的光子有軌道角動量mħ,其中的正整數m也就是光束中央渦旋的強度。圓偏振光的自旋角動量可以被轉換成軌道角動量[3]。 創造光學渦旋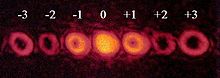 有許多的方式可以產生超几何高斯光束,靜態螺旋相位板(Static spiral phase plate, SPP)、電腦產生的全息摄影、模式轉換(Mode conversion)、q板、s板、空間光調製器及可變形反射鏡等。 應用光學渦旋可用在許多應用中,例如以往只能直接偵測的太陽系外行星可以用旋風星冕儀觀測。光鑷可以用在處理像細胞大小的物體等,受激發射損耗顯微鏡中也有到光學渦旋的技術。 相關條目參考資料
外部連結
|
