Koefisien
|
Read other articles:

Bunga pukul empat Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Core Eudikotil Ordo: Caryophyllales Famili: Nyctaginaceae Genus: Mirabilis Spesies: M. jalapa Nama binomial Mirabilis jalapa mial_authority = L. Bunga pukul empat atau Mirabilis Jalapa merupakan spesies tanaman hias yang paling umum ditanam dari genus Mirabilis, dan tersedia dalam berbagai warna. Mirabilis dalam Bahasa Latin berarti indah dan Jalapa yang merupakan na…

Massimiliano Allegri Allegri alla guida della Juventus nel 2018 Nazionalità Italia Altezza 183 cm Peso 75 kg Calcio Ruolo Allenatore (ex centrocampista) Squadra Juventus Termine carriera 2003 - giocatore Carriera Squadre di club1 1984-1985 Cuoiopelli7 (0)1985-1988 Livorno29 (0)1988-1989 Pisa2 (0)1989-1990 Pro Livorno32 (8)1990-1991 Pavia29 (5)1991-1993 Pescara64 (16)1993-1995 Cagliari46 (4)1995-1997 Perugia41 (10)1997 Padova21 (0)1997-199…

Harold Brown Menteri Pertahanan Amerika Serikat ke-14Masa jabatan21 Januari 1977 – 20 Januari 1981PresidenJimmy Carter PendahuluDonald RumsfeldPenggantiCaspar WeinbergerPresiden Institut Teknologi California ke-3Masa jabatan1969–1977 PendahuluLee Alvin DuBridgePenggantiRobert F. Christy (pelaksana tugas)Menteri Angkatan Udara Amerika Serikat ke-8Masa jabatan1 Oktober 1965 – 15 Februari 1969PresidenLyndon B. Johnson PendahuluEugene M. ZuckertPenggantiRobert SeamansDirektur…

American politician (1854–1919) William T. Haines49th Governor of MaineIn officeJanuary 1, 1913 – January 6, 1915Preceded byFrederick W. PlaistedSucceeded byOakley C. CurtisMaine Attorney GeneralIn office1897–1900GovernorLlewellyn PowersPreceded byFrederick A. PowersSucceeded byGeorge M. SeidersMember of the Maine SenateIn office1888-1892 Personal detailsBornWilliam Thomas Haines(1854-08-07)August 7, 1854Levant, MaineDiedJune 4, 1919(1919-06-04) (aged 64)Augusta, MainePol…

American politician Marty HarbinMember of the Georgia State Senatefrom the 16th districtIncumbentAssumed office January 12, 2015Preceded byRonnie Chance Personal detailsBorn (1955-04-02) April 2, 1955 (age 69)Atlanta, GeorgiaPolitical partyRepublican Maurice H. Harbin (born April 2, 1955) is an American politician who has served in the Georgia State Senate from the 16th district since 2015.[1][2] In January 2024, Harbin co-sponsored S.B. 390, which would withhold go…

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) دوري السوبر الألباني 1934 تفاصيل الموسم دوري السوبر الألباني النسخة 5 البلد ألبانيا التاريخ بداية:…

ينطبق تعبير فن الإسلام أو الفن الإسلامي[1] على الإنتاج الفني الذي وقع منذ الهجرة (622 ميلادي) حتى القرن التاسع عشر في منطقة تمتد من إسبانيا إلى الهند التي يسكنها فئات من الثقافة الإسلامية.[2]ضريح تاج محل,الهند,1630ظهر الفن في العالم الإسلامي مقدماً وحدة أسلوبية تقتضي بنقل …

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Budaya Singapura – berita · surat kabar · buku · cendekiawan · JSTOR (Maret 2022) Lapangan pusat Raffles Place Mahkamah Agung Lama Singapura Kehidupan di Singapura Budaya Tarian Demografi Berkendara Ekonomi Pend…

John NewlandsLahir26 November 1837 (1837-11-26)Lambeth, Surrey, Inggris,Britania RayaMeninggal29 Juli 1898 (1898-07-28UTC16) (aged 60)Lower Clapton, Middlesex, Inggris, Britania RayaKebangsaanInggrisWarga negaraBritaniaAlmamaterRoyal College of ChemistryDikenal atasTabel periodik, hukum oktafPenghargaanDavy Medal (1887)Karier ilmiahBidangKimia analisis Tempat lahir Newlands di West Square, Lambeth. John Alexander Reina Newlands (26 November 1837 – 29 Juli 1898) adalah seorang ki…

Tyler James WilliamsWilliams saat pemutaran perdana Let It Shine.Lahir9 Oktober 1992 (umur 31)Westchester County, New York, Amerika Serikat[1]PekerjaanAktorraperTahun aktif1996-sekarang Tyler James Williams (lahir 9 Oktober 1992) adalah aktor dan rapper asal Amerika Serikat. Dia memulai karirnya sebagai aktor cilik, membuat beberapa penampilan di Saturday Night Live, Little Bill dan Sesame Street.[2] Williams kemudian menjadi terkenal karena memainkan peran Chris Rock d…

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые ры�…

Internazionali Femminili di Palermo 2013 Sport Tennis Data 6 luglio – 14 luglio Edizione 26a Superficie Terra rossa Campioni Singolare Roberta Vinci Doppio Kristina Mladenovic / Katarzyna Piter 2012 2019 Gli Internazionali Femminili di Palermo 2013 (conosciuti anche come Snai Open) sono stati un torneo femminile di tennis giocato sulla terra rossa. È stata la 26ª edizione degli Internazionali Femminili di Palermo, che fa parte della categoria International nell'ambito del WTA Tour 2013. Si s…

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、蘭&…
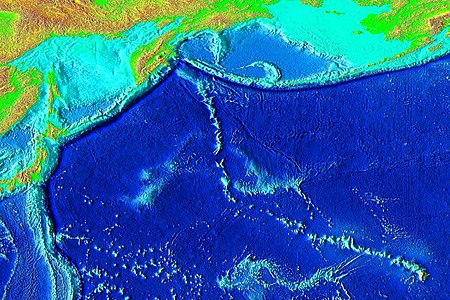
Flat topped seamount of the Hawaiian-Emperor seamount chain in the northern Pacific Ocean Yuryaku GuyotElevation of the Pacific seafloor, showing the Hawaiian-Emperor seamount chain, including Yuryaku Seamount a bit off of the V. The sharp V separates the Hawaiian Ridge from the older Emperor Seamount portion of the chain. Yuryaku is the center/northernmost and most elongated of the small grouping of three fairly small volcanoes near the bend.LocationGroupEmperor seamountsCoordinates32°40.20′…

Pier railway and ferry in Hampshire, England Hythe Pier, Railway and FerryOverviewCoordinates50°52′29″N 1°23′37″W / 50.8746°N 1.3935°W / 50.8746; -1.3935Stations2ServiceTypePier, railway and ferryOperator(s)Blue Funnel Ferries LtdRolling stock2 locomotives4 bogie carriages1 flat car1 tank car Listed Building – Grade IIOfficial nameHythe PierDesignated17 August 2021Reference no.1476460 TechnicalTrack gauge2 ft (610 mm) Route map Legend Fe…

Samuel Fuller Samuel Fuller (Worcester, 12 agosto 1912 – Los Angeles, 30 ottobre 1997) è stato un regista, sceneggiatore e produttore cinematografico statunitense. Con il suo stile violento e visionario è stato un profondo innovatore del cinema di genere americano[1]. Indice 1 Biografia 1.1 A Hollywood e la seconda guerra mondiale 1.2 La produzione 1.3 Come attore 2 Omaggi 3 Riconoscimenti 4 Filmografia 4.1 Regista 4.1.1 Cinema 4.1.2 Televisione 4.2 Attore 5 Note 6 Bibliografia 7 Alt…
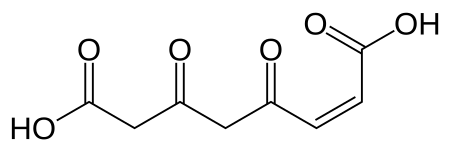
4-Maleylacetoacetic acid Names Preferred IUPAC name (2Z)-4,6-Dioxooct-2-enedioic acid Other names 4-Maleylacetoacetate Identifiers CAS Number 5698-52-2 N 3D model (JSmol) Interactive image ChEBI CHEBI:47904 Y ChEMBL ChEMBL1743220 N ChemSpider 4444078 Y KEGG C01036 Y PubChem CID 5280393 UNII 5ET93TW8TE Y InChI InChI=1S/C8H8O6/c9-5(1-2-7(11)12)3-6(10)4-8(13)14/h1-2H,3-4H2,(H,11,12)(H,13,14)/b2-1- YKey: GACSIVHAIFQKTC-UPHRSURJSA-N YInChI=1/C8H8O6/c9-5(1-…

VCP-1 Role USAAS Pursuit prototypeType of aircraft Manufacturer Engineering Division Designer Alfred V. Verville First flight 11 June 1920 Number built 2 Variants Verville-Packard R-1 The Verville VCP was an American single-engined biplane fighter aircraft of the 1920s. A single example of the VCP-1 was built by the United States Army Air Service's Engineering Division, which was later rebuilt into a successful racing aircraft, while a second, modified fighter was built as the PW-1. Design and d…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMPN 1 SusukanlebakInformasiJenisNegeriJumlah kelasVII, VIII, IXRentang kelasVII A-H, VIII A-H, IX A-HStatusSekolah Menengah Pertama NegeriNEM terendah-NEM tertinggi-Nilai masuk rata-rata-AlamatLokasiJl Abdurahman saleh no.24 Pasawahan, Susukanlebak…

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸類�…














