| دالة خطية
|
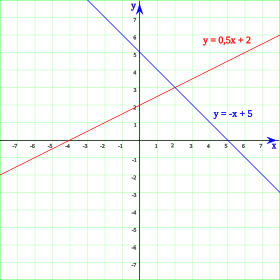 تمثيل الدوال تمثيل الدوال  و و  تمثيل الدوال  و و 
|
| تدوين |
 |
| دالة عكسية |
 إذا كان إذا كان  |
| مشتق الدالة |
 |
مشتق عكسي
(تكامل) |
 |
| الميزات الأساسية
|
| مجال الدالة |
 |
| المجال المقابل |
 إذا كان إذا كان  |
| قيم محددة
|
| القيمة/النهاية عند الصفر |
 |
| نهاية الدالة عند +∞ |
 إذا كان إذا كان   إذا كان إذا كان 
|
| نهاية الدالة عند -∞ |
 إذا كان إذا كان   إذا كان إذا كان 
|
| جذور الدالة |
 |
| نقاط ثابتة |
 إذا كان إذا كان  |
تعديل مصدري - تعديل  |
في الرياضيات، الدَالّة الخطية (ملاحظة 1) هي دالة حقيقية يتم الحصول عليها عن طريق جمع وضرب المتغير في الثوابت. تكتب أي دالة خطية على الشكل التالي:

حيث a و b عددان معلومان لا يتعلقان بالمتغير x.
عندما يكون a و b عددين حقيقيين، يكون الرسم البياني لهذه الدالة مستقيما ميله هو a و b هو نقطة تقاطعه مع المحور y. قد يكون هذا المستقيم مائلا، وقد يكون موازيا لمحور x فيقال حينئذ عنها دالة ثابتة.
في المغرب العربي، يسمى هذه الدالة بالدالة التآلفية حيث b يكون لا يساوي الصفر؛ أما إذا كان يساوي الصفر، تسمى هذه الدالة بالدالة الخطية.
أشكال الاقتران الخطي
- اقتران ثابت:هو أحد أنواع الاقتران الخطي
- اقتران محايد:هو أحد أنواع الاقتران الخطي
- اقتران جذري:هو أحد أنواع الاقتران الخطي
الاقتران الثابت
حيث إن المجال ح، والمدى هو b فقط.
مثال : f(x)= 2
f(2)= 2 / f(1)= 2 / f(4)= 2
 ق(س)= 2
ق(س)= 2
الاقتران المحايد
- صورته العامة : f(x)= x
- مجاله : ح، والمدى : ح
f(2)= 2 / f(1)=1 / f(0)= 0 / f(4)= 4
 ق(س)= س
ق(س)= س
ا
الاقتران الجذري
- صورته العامة : ax + b √
- معرف بشرط أن ax + b ≥ صفر .
- مجاله : لا بد من دراسة إشارة المقدار ax + b عن طريق مساواته بالصفر من خلال :
1) س ≥ (-ب )/أ
- المدى : [0 , ∞) , إذا ما ادخلت عليه إشارة خارج الجذر .
مثال : (2x - 4)√
مجاله : نحتاج لدراسة الإشارة من خلال : ب= -4 أ= 2
1) س ≥ (-ب )/أ , -(-4) / 2 = 2 ,,, أذن س ≥ 2
- المجال [2 , ∞ )
- المدى [ 0 , ∞ )
 ق(س)=(2س-4)√
ق(س)=(2س-4)√
- أو لدراسة إشارة الاقتران الجذري نقوم بمساواة الاقتران الذي تحت الجذر بالصفر
مثال : ادرس إشارة ق(س)= 3س-6√ الحل: 1- نساويها بالصفر = 3x-6 = 0
- 3x-6=0 (اجمع 6 للطرفين )
- 3x = 6 (اقسم على 3)
- x = 2
فإن مجال f(x) يكون [2،∞) والمدى [ 0،∞)
انظر أيضًا
ملاحظات
ملاحظة 1: أو التابع الخطي أو الاقتران الخطي.
مراجع
- Arfken, Mathematical Methods for Physicists, 1985, pg. 201
- كتاب الإحداثيات المنحنيات المستقيمات الاقترانات النهايات 61
- WolfarmMathworld.com [1]




















