قطع زائد

القُطوعُ المخروطيَّةُ

هذه المقالةُ جزءٌ من سلسلةِ القطوع المخروطية
قطع مكافئ
المعادلة	${\displaystyle y^{2}=4ax\,}$
الانحراف المركزي(${\displaystyle e}$)	${\displaystyle 1\,}$
البعد البؤري(${\displaystyle l}$)	${\displaystyle 2a\,}$
قطع زائد
المعادلة	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
الانحراف المركزي (${\displaystyle e}$)	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$
البعد البؤري(${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
قطع ناقص
المعادلة	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
الانحراف المركزي (${\displaystyle e}$)	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$
البعد البؤري (${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
دائرة (حالة خاصة من القطع الناقص)
المعادلة	${\displaystyle x^{2}+y^{2}=a^{2}\,}$
الانحراف المركزي (${\displaystyle e}$)	${\displaystyle 0}$
البعد البؤري (${\displaystyle l}$)	${\displaystyle a}$
• • •
ع ن ت

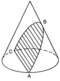
القَطْع الزائد^[1] أو القِطْع الزائد^[2] (Hyperbola) (في اللغة الإغريقية ὑπερβολή) أو الهَذْلُول^[3]، هو أحد أنماط القطوع المخروطية (conic sections).

القطع الزائد ناتج عن قطع المخروط بمستو في أحد نصفي المخروط، وهو الذي يكون اختلافه المركزي أكبر من الواحد الصحيح، ويمكن تعريفه بعبارة أخرى: وهو القطع الذي ينشأ عن قطع سطح مخروطي دائري قائم وامتداده من جهة رأسه بمستو يميل على مستوى دليله بزاوية أكبر من زاوية ميل أحد الرواسم على مستوى الدليل.

ويعرف أيضا على أنه مجموعة النقاط التي تتميز بكون فرق مسافة هذه النقاط عن نقطتين ثابتتين (تدعى البؤرتين) هو عدد ثابت.

ونقول أن القطعان الزائدان متشابهين (Similar)، إذا كان اختلافهما المركزيان متساويين، ويكون قطعان زائدان مترافقين إذا كان المحور المستعرض لأحدهما هو المحور المرافق للآخر والمحور المرافق للأول هو المستعرض للآخر.

المعادلة للقطع الزائد هي:
${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ إذا هي تقطع المحور الأفقي x
و ${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}$ إذا هي تقطع المحور الرأسي y
حيث a هو قيمة مطلقة ل x إذا المعادلة تقطع المحور x و b قيمة مطلقة ل y إذا المعادلة تقطع المحور y
وكما في الصورة السابقة: الجزء من خط التقارب المائل هو (a, b) و${\displaystyle b={\sqrt {a^{2}+c^{2}}}}$
حيث c هو أقصر مسافة من نقطة الأصل إلى البؤرة B2
ومعادلة الخط التقاربي ${\displaystyle y=\pm x\times {\frac {a}{b}}}$ للمعادلة ${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}$

و${\displaystyle y=\pm x\times {\frac {b}{a}}}$ للمعادلة ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$.[4]

القطع الزائد في الهندسة الوصفية، يمكن الحصول عليه:

• عن طريق قطع مخروط دوراني K بمستوى موازي لاثنين من راسمين سطح K.
• كمحل هندسي لمراكز الدوائر الماسة دائرتين معلومتين Θ Δ، في الظروف التي تكون فيها تلك الدائرتين Θ Δ متقاطعتين أو خارجتين عن بعضهما البعض (أي ان لا تكون الواحدة داخل الأخرى) وان يكون مختلف نصف قطرهما. في الحالة التي يكون فيها تساوي بين الدائرتين Θ Δ, المحل الهندسي الناتج يكون مكون من نقاط تنتمي إلى خط مستقيم الذي ينطبق مع محور تماثل الدائرتين.
  • بشكل عام، يين اهليجين متشابهين ومتحدي المستوى، يتم تعريف القطع الناقص بالمحل الهندسي لمراكز الاهاليج المتشابهة للاهليجين المعلومين بحيث يكونوا متماسين لنفس الاهليجين.

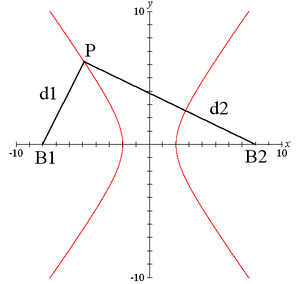
يُعرَّف القطع الزائد كمحل هندسي للنقاط التي يكون فرق ابعادها عن البؤر ثابت.

معلوم قطع زائد. مطلوب تحديد محاور وبؤر وخطوط التقارب

الخطوات

1. نحدد المركز C كتقاطع بين الخطوط التي تمر بنقاط منتصف زوجين من الأوتار المتوازية
2. نرسم من C محوري القطع الزائد Λ بحيث يكونان متعامدين على بعضهما البعض
3. نحدد الرؤوس V'و V" كتقاطع بين المحور العرضي والقطع الزائد Λ
4. نحدد البؤر F', F" كتقاطع بين الدائرة Θ والمحور العرضي. يتم تحديد الدائرة Θ عن طريق 3 نقاط: نختار واحدة منها على Λ , ونحدد نقطتين منها كتقاطع بين المحور غير العرضي وبين خطين يمران بالنقطة A. واحد من الخطين متماس Λ في النقطة A ، والاخر عمودي على المتماس.
5. لتحديد الخطوط المتقاربة نرسم دائرة Β نصف قطرها يساوي F'_C (أو F«_C). نرسم خطين متماسين Λ في الرؤوس V'و V». ومن نقاط تقاطعهما مع الدائرة Β نرسم الخطين المتقاربين. اللذين يمران أيضا بالنقطة C.

ملاحظة: الخط المتماس قطع زائد دلتا في نقطة ب تنتمي لديلتا، يحدد كمنصف الزاوية التي رأسها في ب وضلعيها يمران ببؤرتي دلتا^{[5] [6]}

معلوم قطع زائدة دلتا على مستوى الأرض. مطلوب تحديد المخروط الذي مقطعه يتطابق مع المخروطية دلتا.

لحل هذه المسألة نقوم بإسقاط رؤوس القطع الزائد على خط الأرض. ومن الإسقاطات نمرر خطوط موازية لخطوط التقارب (Asymptote). نقوم بتوليد المخروط الدائري الذي رواسمه (generatrixes) هي خطوط التقارب. - وأخيرا نقطع المخروط بمستوى الأرض للحصول على المخروطية المطلوبة.

• 
  يُعرف القطع الزائد بالموقع الهندسي للنقاط التي تكون قيمة اختلاف مسافاتها بالنسبة للبؤرتين عدد ثابت
• 
  إنشاء هندسي لقطع زائد عن طريق مخروطيته الارتدادية
• 
  لا تتطابق صورة مركز القطع الزائد الموضوعي مع مركز صورة القطع الزائد نفسه
• 
  اجراء هندسي سريع ودقيق لرسم قطع زائد، معلومة خمس نقاط, 3 منها غير متسامتة

• قطع مكافيء.
• قطع ناقص.
• دالة زائدية
• قطع مخروطي
• اختلاف مركزي (رياضيات)