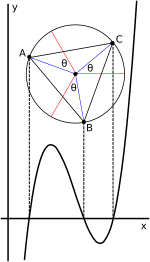
معادلة تكعيبية
|
Read other articles:

Bérénice BejoBejo di acara Festival Film Cannes 2016Lahir7 Juli 1976 (umur 47)Buenos Aires, ArgentinaKebangsaanPrancisTahun aktif1993–sekarangSuami/istriMichel HazanaviciusAnak2 Bérénice Bejo (pengucapan bahasa Prancis: [be.ʁe.nis be.ʒo]; lahir 7 Juli 1976) adalah seorang aktris Prancis yang berperan sebagai Christiana dalam film tahun 2001 A Knight's Tale dan sebagai Peppy Miller dalam film tahun 2011 The Artist. Penampilannya di film The Artist membuat dirinya menerima n…

Chiryū 知立市Kota BenderaLambangLocation of Chiryū in Aichi PrefectureNegara JepangWilayahChūbuPrefekturAichiPemerintahan • WalikotaIkuo HayashiLuas • Total16,31 km2 (630 sq mi)Populasi (Oktober 1, 2019) • Total71.992 • Kepadatan4,414/km2 (11,43/sq mi)Zona waktuUTC+9 (Japan Standard Time)Simbol kota • PohonZelkova serrata• BungaIris laevigataNomor telepon0566-83-1111Alamat3-1 Hiromi, Chiryū-shi, Ai…

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属的�…

لمعانٍ أخرى، طالع ويليام جيبسون (توضيح). ويليام جيبسون معلومات شخصية الميلاد سنة 1815 تاريخ الوفاة فبراير 1890 (74–75 سنة) مواطنة كندا مناصب عضو مجلس العموم الكندي[1] في المنصب12 أكتوبر 1872 – 16 سبتمبر 1878 الحياة العملية المهنة سياسي[1] الحزب …

Sebuah rudal Exocet ditembakkan. Bom berpandu laser. Pengendali giroskopik. Depan: Pengendali giro three axis SH-300. Digunakan orbiter Buran. Tengah: Pengendali giro menegak flight rocket R-7. Rudal hipersonik Shaurya dengan kecepatan Mach 7,5 walau di ketinggian rendah, Panduan guidance adalah sistem pandu arah lembam giro laser cincin dan akselerometer dengan ketepatan CEP 20 m sampai 30 m. VLS MK41 DDG-62 Fitzgerald VLS pada kapal selam Oklahoma City Perbandingan pemasangan rudal pada VLS. P…

Branford Marsalis Branford Marsalis (lahir 26 Agustus 1960) merupakan seorang penyanyi jazz dan pemain saksofon berkebangsaan Amerika Serikat. Dia merupakan orang yang tertua daripada enam keponakan mereka: Wynton Marsalis, Ellis Marsalis III, Delfeayo Marsalis, Mboya Kinyatta, dan Jason Marsalis. Diskografi 2006 Braggtown 2004 A Love Supreme Live - (DVD/CD) 2004 Eternal 2003 Romare Bearden Revealed 2002 Footsteps of our Fathers 2001 Creation 2000 Contemporary Jazz 1999 Requiem 1997 Music Evolut…

Turkish Graeco-Roman style wrestler Hamza YerlikayaPersonal informationNationalityTurkishBorn (1976-06-06) June 6, 1976 (age 47)Kadıköy, Istanbul, TurkeyHeight1.76 m (5 ft 9 in)Weight84 kg (185 lb)SportSportSport wrestlingEventGreco-Roman wrestlingClubIstanbul BB SKTurned pro1992Retired2007 Medal record Event 1st 2nd 3rd Olympic Games 2 0 0 World Championship 3 1 1 European Championships 8 1 0 World Cup 3 1 0 Mediterranean Games 1 0 1 Other 5 2 2 Total 22 5 4 Men'…

American variety show (1946–1958) Arthur Godfrey's Talent ScoutsCountry of originUnited StatesLanguage(s)EnglishStarringArthur GodfreyOriginal releaseJuly 2, 1946 (1946-07-02) –October 1, 1956 (1956-10-01)Sponsored byLipton Tea Arthur Godfrey's Talent Scouts (also known as Talent Scouts) was an American radio and television variety show which ran on CBS from 1946 until 1958. Sponsored by Lipton Tea, it starred Arthur Godfrey, who was also hosting Arthur Godfrey and His Friends…

坐标:43°11′38″N 71°34′21″W / 43.1938516°N 71.5723953°W / 43.1938516; -71.5723953 此條目需要补充更多来源。 (2017年5月21日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:新罕布什尔州 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(…

Jan MatejkoLahirJan Mateyko24 Juni 1838Kota Merdeka KrakówMeninggal1 November 1893(1893-11-01) (umur 55)Kraków, Polandia AustriaMakamPemakaman RakowickiKebangsaanPolandiaPendidikanSekolah Seni Rupa KrakówAkademi Seni Rupa MünchenDikenal atasSeni lukisKarya terkenalBattle of GrunwaldStańczykThe Prussian HomageThe Hanging of the Sigismund bellGerakan politikLukisan sejarahSuami/istriTeodora Matejko Jan Alojzy Matejko (pengucapan bahasa Polandia: [jan aˈlɔjzɨ maˈtɛjko]; juga dik…

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6] 得…

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Miss Universe Canada 2018 – news · newspapers · books · scholar · JSTOR (August 2019) (Learn how and when to remove this message) Beauty pageant Miss Universe Canada 2018DateAugust 18, 2018[1]PresentersSonny BorrelliChelsae DurocherVenueJohn Bassett Theatre, Metro Toronto Convention Centre, TorontoBro…

Burmese television series Nway Lal Nya Yae La MinPosterBurmeseနွေလယ်ညရဲ့လမင်း GenreDramaBased onMaung Nway Oo Nae Ma Phoo Waiby Le Dwin Thar Saw ChitScreenplay byHein Zaw OoThet ZunKhin Maung KyawDirected byHein Ko KoStarringPhone Shein KhantChue LayThan Thar NyiHein YatuNet Shine KoTheme music composerZa War (ဇဝါ)Opening themeHtun Lin Mae La Min (ထွန်းလင်းမယ့်လမင်း)Ending themeHtun Lin Mae La Min (ထွန်းလင်�…
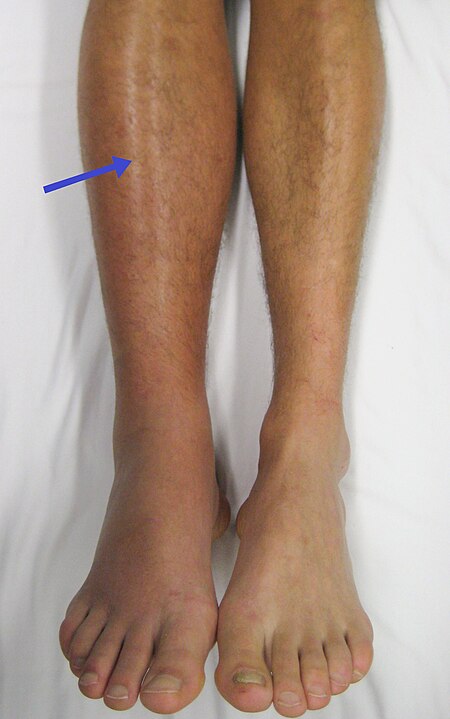
Abnormality of blood coagulation Medical conditionThrombophiliaAn ultrasound image demonstrating a blood clot in the left common femoral vein.SpecialtyHematology Thrombophilia (sometimes called hypercoagulability or a prothrombotic state) is an abnormality of blood coagulation that increases the risk of thrombosis (blood clots in blood vessels).[1][2] Such abnormalities can be identified in 50% of people who have an episode of thrombosis (such as deep vein thrombosis in the…

Помаранчева стрічка — символ української помаранчевої революції 2004 року Символічна стрічка (англ. Awareness ribbon) — невеликий шматок стрічки, складений у петлю. Використовується для демонстрації ставлення носія стрічки до якогось питання або проблеми, вираження підтрим…
Part of a series on the History of Palestine Prehistory Natufian culture Pre-Pottery Tahunian Ghassulian Jericho Ancient history Canaan Phoenicia Egyptian Empire Ancient Israel and Judah (Israel, Judah) Philistia Philistines Neo-Assyrian Empire Neo-Babylonian Empire Achaemenid Empire Classical period Seleucus Antigonus Hasmonean dynasty Herodian kingdom Province of Judea Syria Palaestina Byzantine Empire(Palaestina Prima / Secunda) Islamic rule Muslim conquest Rashidun (Jund Filastin, J…

乔冠华 中华人民共和国外交部部长 中国人民对外友好协会顾问 任期1974年11月—1976年12月总理周恩来 → 华国锋前任姬鹏飞继任黄华 个人资料性别男出生(1913-03-28)1913年3月28日 中華民國江蘇省盐城县逝世1983年9月22日(1983歲—09—22)(70歲) 中华人民共和国北京市籍贯江蘇鹽城国籍 中华人民共和国政党 中国共产党配偶明仁(1940年病逝) 龚澎(1970年病逝) 章含之�…

Zigo Rolanda Ketua Dewan Perwakilan Rakyat Daerah Kabupaten Solok SelatanPetahanaMulai menjabat 25 September 2019PendahuluSidik IlyasPenggantiPetahana Informasi pribadiLahir10 Desember 1991 (umur 32)Rimbo Tangah, Lubuk Gadang, Sangir, Solok Selatan, Sumatera BaratPartai politikGolkarOrang tuaKhairunas (ayah)Sunting kotak info • L • B Zigo Rolanda, S.E. (lahir 10 Desember 1991) adalah seorang politisi Indonesia yang merupakan politisi Partai Golongan Karya yang menjabat seb…

Pace di LodiL'Italia all'indomani della firma della pace di Lodi (1454)ContestoConflitto tra Ducato di Milano e Repubblica di Venezia con i rispettivi alleati[1] Firma9 aprile[1][2] 1454 LuogoPalazzo Broletto, Lodi[2], Ducato di Milano CondizioniRestituzione di Bergamasco e Bresciano alla Repubblica di Venezia[1]; raggiungimento della stabilità politica in Italia[3] e successione di Francesco Sforza al Ducato di Milano[1] NegoziatoriAngelo…

2009 terror attack in Peshawar, Pakistan 28 October 2009 Peshawar Market BombingLocationPeshawar, PakistanCoordinates34°00′31″N 71°34′32″E / 34.008723°N 71.575552°E / 34.008723; 71.575552Date28 October 2009 1300 hrs (UTC+5)TargetMeena BazarAttack typeCar bombing,[1] fireWeapons150 kilograms (330 lb) of explosiveDeaths137[2][failed verification]Injured213[1] The 28 October 2009 Peshawar bombing occurred in Peshawar, Pakistan…
















![{\displaystyle {\begin{aligned}x_{1}=&-{\frac {b}{3a}}\\&-{\frac {1}{3a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d+{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\&-{\frac {1}{3a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d-{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\x_{2}=&-{\frac {b}{3a}}\\&+{\frac {1+i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d+{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\&+{\frac {1-i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d-{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\x_{3}=&-{\frac {b}{3a}}\\&+{\frac {1-i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d+{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\&+{\frac {1+i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d-{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef8fdcb363d20258b4ec96f33fc248aae912c9ff)











![{\displaystyle u={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a60cb84513229417c12823f420364648b12f0bd)
![{\displaystyle v={\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/391c58de78809a3613528fed4257a9eb6662cea4)










![{\displaystyle u=0{\text{ و }}v=-{\sqrt[{3}]{q}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fd3f27604bd4b1ea1784a2ecabc984c15cc41f1)






![{\displaystyle t1=2*u=2{\sqrt[{3}]{-{\tfrac {q}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdaf40fe4d0feee27dabf49f28f449903f4af434)
![{\displaystyle t2=-u=-{\sqrt[{3}]{-{\tfrac {q}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12d83ffeb6452b84d533c43ef72f3dba3d95eae0)

![{\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57102b328503b04914d43ce3ab469e53c6fad58d)
![{\displaystyle {\sqrt[{3}]{{~}^{~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf)