Körper (Algebra)
|
Read other articles:

Process in winemaking A winemaker running a paper chromatography test to determine whether a wine has completed malolactic fermentation Malolactic conversion (also known as malolactic fermentation or MLF) is a process in winemaking in which tart-tasting malic acid, naturally present in grape must, is converted to softer-tasting lactic acid. Malolactic fermentation is most often performed as a secondary fermentation shortly after the end of the primary fermentation, but can sometimes run concurre…

Christopher LoriaLahir09 Juli 1960 (umur 63)Newton, Massachusetts, ASStatusPurnawirawanKebangsaanAmerika SerikatPekerjaanPilot uji cobaKarier luar angkasaAntariksawan NASAPangkatKolonel Korps Marinir Amerika SerikatSeleksi1996 NASA GroupMisiTidak ada Christopher Joseph Gus Loria (lahir 9 Juli 1960) adalah seorang purnawirawan Kolonel Korps Marinir Amerika Serikat dan antariksawan NASA yang purna tugas karena alasan kesehatan. Ia awalnya direncanakan untuk ikut STS-113 sebagai pilot. Namun, …

Alga merahRentang fosil: Mesoproterozoikum–sekarang[1] Had'n Arkean Proterozoikum Pha. Klasifikasi ilmiah Domain: Eukariota (tanpa takson): Archaeplastida Filum: RhodophytaWettstein, 1922 kemungkinan kelas Florideophyceae Bangiophyceae Cyanidiophyceae Alga merah atau Rhodophyta (/roʊˈdɒf[invalid input: 'ɨ']tə/ roh-DOF-fit-tə atau /ˌroʊdəˈfaɪtə/ ROH-də-FY-tə; dari Bahasa Yunani Kuno: ῥόδον rhodon, mawar and φυτόν phyton, tumbuhan) adalah salah satu filum dari al…

Dornier Do 228LGW Do 228-200TipePesawat penumpang regionalTerbang perdana21 Maret 1981Diperkenalkan1982Tahun produksi1981-19982009–Jumlah produksi270Acuan dasarDornier Do 28 Do 228 milik Angkatan Laut Jerman dalam corak lama. Dek penerbangan Kabin penumpang Penjaga Perbatasan Finlandia Do 228 di Bandar Udara Helsinki-Malmi. Pesawat eksperimen Do 28 TNT pada tahun 1980 Dornier 228 adalah pesawat turboprop bermesin ganda STOL serbaguna, yang dibangun oleh Dornier GmbH (kemudian bernama DASA Dorn…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: LK…

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: WFRG-FM – news · newspapers · books · scholar · JSTOR (June 2014) (Learn how and when to remove this template message) Radio station in Utica, New YorkWFRG-FMUtica, New YorkBroadcast areaUtica-Rome, New YorkFrequency104.3 MHzBrandingBig Frog 104ProgrammingFormatCountryAffiliationsC…

Dongeng Negeri Cintaalbum studio karya Fariz R.M.Dirilis24 november 1997Direkam1996-pertengahan 1997StudioFariz R.M. Studio, Bintaro Jaya, JakartaStudio Supranada, JakartaGenrePopDurasi50:12LabelSupranada Abadi RecordsProduserFariz R.M.Ishak PudjiantoSukmana HalimKronologi Fariz R.M. Romantic (1994)Romantic1994 Dongeng Negeri Cinta (1997) Kronologi (1997) Singel dalam album Dongeng Negeri Cinta Batas Rindu Kronologi1997 Dongeng Negeri Cinta adalah album kelima belas dari musisi Fariz R.M. ya…

Cette page concerne l'année 1944 (MCMXLIV en chiffres romains) du calendrier grégorien. Pour l’article homonyme, voir 1944 (chanson). Chronologies Into the Jaws of Death, photographie des troupes américaines avançant dans l'eau d'Omaha Beach, le 6 juin 1944.Chronologie de la Seconde Guerre mondiale Jan - Fév - Mar - Avr - Mai - Juin Juil - Aoû - Sep - Oct - Nov - Déc Chronologie dans le monde 1941 1942 1943 1944 1945 1946 1947Décennies :1910 1920 1930 1940 …

Johannes Baumann Presiden Konfederasi Swiss Ke-90Masa jabatan1 Januari 1938 – 31 Desember 1938PendahuluGiuseppe MottaPenggantiPhilipp EtterAnggota Dewan Federal SwissMasa jabatan22 Maret 1934 – 31 Desember 1940PendahuluHeinrich HäberlinPenggantiKarl Kobelt Informasi pribadiLahir(1874-11-27)27 November 1874Meninggal8 September 1953(1953-09-08) (umur 78)KebangsaanSwissSunting kotak info • L • B Johannes Baumann (27 November 1874 – 8 September 1953) adala…

Joachim PrinzBiographieNaissance 10 mai 1902BierdzanyDécès 30 septembre 1988 (à 86 ans)LivingstonNationalités allemandeaméricaineFormation Université de GiessenSéminaire théologique juif de BreslauActivité RabbinAutres informationsMembre de Blau-WeissSite web (en) www.joachimprinz.commodifier - modifier le code - modifier Wikidata Joachim Prinz né le 10 mai 1902 à Burckhardtsdorf en Haute-Silésie et mort le 30 septembre 1988 à Livingston dans l'État du New Jersey, est un …

South Korean actress (born 1979) In this Korean name, the family name is Bae. Bae DoonaBae in December 2023Born (1979-10-11) October 11, 1979 (age 44)Seoul, South Korea[1]EducationKonkuk University (Department of Film Arts)OccupationsActressphotographerYears active1999–presentAgentGoodman Story Ent.ParentKim Hwa-young [ko] (mother)Korean nameHangul배두나Hanja裵斗娜Revised RomanizationBae Du-naMcCune–ReischauerPae Tuna Websitedoona.net Bae Doo-na (Korean&#…

StumpWMStumpWM, a window manager in Common LispDeveloper(s)Shawn BettsStable release23.11[1] / 26 November 2023 Repositorygithub.com/stumpwm/stumpwm.git Written inCommon LispOperating systemUnix-likeTypeWindow managerLicenseGPL-2.0-or-later[2]Websitestumpwm.github.io StumpWM is a tiling window manager that was created when developer Shawn Betts found ratpoison growing increasingly large and lispy. Intended as a successor to ratpoison, StumpWM is released under the terms of …

For other uses, see Yuncheng (disambiguation). Not to be confused with Yancheng. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Yuncheng – news · newspapers · books · scholar · JSTOR (August 2012) (Learn how and when to remove this message) Prefecture-level city in Shanxi, People's Republic of ChinaYuncheng �…

Questa voce o sezione sull'argomento imprenditori è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. André-Gustave Citroën André-Gustave Citro�…
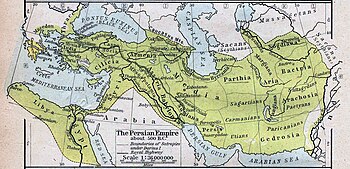
Disambiguazione – Se stai cercando la tragedia di Eschilo, vedi I Persiani. Disambiguazione – Se stai cercando l'Impero Persiano, vedi Persia. Questa voce o sezione sugli argomenti storia antica e Asia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei progetti di riferimento 1, 2. PersianiAbbigliamento di un nobile e dei suoi solda…

городской округБорисоглебский городской округ Флаг 51°22′00″ с. ш. 42°05′00″ в. д.HGЯO Страна Россия Входит в Воронежскую область Включает 25 населённых пунктов Адм. центр город Борисоглебск История и география Дата образования 2006 год Площадь 1371[1] км² Высот�…

Ini adalah nama Korea; marganya adalah Lee. Pada nama panggung/nama pena, nama belakangnya adalah Seo. Seo Eun-sooSeo Eun-soo pada Februari 2019LahirLee Jeong-min2 Maret 1994 (umur 30)Busan, Korea SelatanAlmamaterUniversitas Kesenian Nasional Korea – AktingPekerjaanAktrisModelTahun aktif2015–sekarangAgenUL Entertainment[1]Nama KoreaHangul서은수 Alih AksaraSeo Eun-suMcCune–ReischauerSŏ ŬnsuNama lahirHangul이정민 Alih AksaraI Jeong-minMcCune–ReischauerI Chŏ…

Flaviviridae Komposisi genom virus ICTVpositive-sense single-stranded RNA virus TaksonomiSuperdomainBiotaDomainVirusFamiliFlaviviridae Tata namaDinamakan berdasarkanFlavivirus Genus Hepacivirus Flavivirus Pegivirus Pestivirus lbs Flaviviridae adalah famili virus yang menyebar melalui vektor artropoda (terutama nyamuk). Famili ini mendapat namanya dari virus demam kuning, salah satu jenis dari virus Flaviviridae; flavus (bahasa Latin) yang berarti kuning. Flaviviridae meliputi genus: Genus Hepaci…

Shakespeare play production Poster for the production. It uses a modern graphical style, reflecting the production's break with the past. The 1970 Royal Shakespeare Company (RSC) production of A Midsummer Night's Dream was directed by Peter Brook, and is often known simply as Peter Brook's Dream. It opened in the Royal Shakespeare Theatre at Stratford-upon-Avon and then moved to the Aldwych Theatre in London's West End in 1971. It was taken on a world tour in 1972–1973. Brook's production of A…

Unincorporated community in Kentucky, United States This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Creswell, Kentucky – news · newspapers · books · scholar · JSTOR (February 2023) Unincorporated community in Kentucky, United StatesCreswellUnincorporated communityCreswellLocation within the state of K…








































![{\displaystyle K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb4d802ca5718a14dc961af8692f35cdfad169b)


































![{\displaystyle K[[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/360aa2d367ac90bc66835442e10c739356f67dba)

![{\displaystyle K[x_{1},x_{2},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf50d57cd977cb0e672d455dd348ea18d7ecdf24)











![{\displaystyle (\mathbb {Z} /p\mathbb {Z} )[X]/(P)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208bc8d71fdeb61297b34fafbc8dd64ba45add20)

![{\displaystyle P\in (\mathbb {Z} /p\mathbb {Z} )[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/657ddb5c6f7e34468e69ef026685e1a99dd529d2)
![{\displaystyle (\mathbb {Z} /p\mathbb {Z} )[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d67499db475fa009dfd134de69c9ea7c1ff033a9)




