Free monoid
|
Read other articles:

Sukhoi Su-1 atau I-330 (Rusia: Сухой Су-1) adalah prototipe pesawat tempur ketinggian tinggi Soviet dibangun pada awal Perang Dunia II. Sebuah versi perbaikan, dinamakan Su-3 (I-360), juga dibangun dan diuji pada tahun berikutnya. Versi keduanya itu diproduksi massal. Pavel O Sukhoi mendirikan OKB (Biro Desan Eksperimental) sendiri pada Desember 1938, dan pada awal tahun berikutnya dia menyetujui sebuah tugas untuk mendesain pesawat tempur altitude-tinggi satu-kursi canggih. Awalnya desai…

Friedrich Melchior, Baron von GrimmNama dalam bahasa asli(de) Friedrich Melchior, Baron von Grimm BiografiKelahiran26 September 1723 Regensburg Kematian19 Desember 1807 (84 tahun)Gotha Duta besar Frankfurt am Main KegiatanPekerjaanWartawan, penulis, music critic (en), kritikus sastra, Encyclopédistes dan diplomat Karya kreatifKarya terkenal(1747) La correspondance littéraire (en) KeluargaOrang tuaJohann Melchior Grimm (en) , Sibylla Margarete Grimm (en) SaudaraUlrich Wilh…

Tembok Besar TiongkokSitus Warisan Dunia UNESCOKriteriaBudaya: i, ii, iii, iv, viNomor identifikasi438Pengukuhan1987 (ke-11)Perluasan2004Tembok Besar Tiongkok atau Tembok Raksasa Tiongkok (Hanzi tradisional: 長城; Hanzi sederhana: 长城; Pinyin: Chángchéng) juga dikenal di Tiongkok dengan nama Tembok Sepanjang 10.000 Li¹ (萬里長城; 万里长城; Wànlĭ Chángchéng) adalah bangunan terpanjang yang pernah diciptakan manusia yang berada di Tiongkok.[1][2][3]…

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (فبراير 2018) السيمافور هو مصطلح كشفي يعني التخاطب عن بعد بواسطة أعلام صغيرة مصنوعة من النسيج…

Katedral Kota PanamaKatedral Agung Primatial Metropolitan Basilika Santa María la AntiguaSpanyol: Catedral Primada Basílica Santa María la Antigua de PanamáKatedral Kota Panama8°57′09″N 79°32′07″W / 8.9525°N 79.5352°W / 8.9525; -79.5352Koordinat: 8°57′09″N 79°32′07″W / 8.9525°N 79.5352°W / 8.9525; -79.5352LokasiCasco Antiguo, Kota PanamaNegaraPanamaDenominasiGereja Katolik RomaSejarahTanggal konsekrasi1796ArsitekturS…

1983 American film directed by Richard Marquand This article is about the film. For other uses, see Return of the Jedi (disambiguation). The Battle for Endor redirects here. For the television film, see Ewoks: The Battle for Endor. Return of the JediTheatrical release poster by Kazuhiko SanoDirected byRichard MarquandScreenplay by Lawrence Kasdan George Lucas Story byGeorge LucasProduced byHoward KazanjianStarring Mark Hamill Harrison Ford Carrie Fisher Billy Dee Williams Anthony Daniels David P…

American baseball player and manager (1898-1983) Baseball player Charlie GrimmGrimm with the Pittsburgh Pirates in 1921First baseman / ManagerBorn: (1898-08-28)August 28, 1898St. Louis, Missouri, U.S.Died: November 15, 1983(1983-11-15) (aged 85)Scottsdale, Arizona, U.S.Batted: LeftThrew: LeftMLB debutJuly 30, 1916, for the Philadelphia AthleticsLast MLB appearanceSeptember 23, 1936, for the Chicago CubsMLB statisticsBatting average.290Hits2,299Home runs79Runs b…

German painter and illustrator (1839–1907) Saint Martin at the City Gates Albrecht Christoph Wilhelm von Diez (17 January 1839, Bayreuth – 25 February 1907, Munich) was a German painter and illustrator of the Munich School.[1] Life He attended a trade school in Munich, followed by the Polytechnic School (precursor of the University of Technology) from 1853 to 1855 and, from 1855, the Academy of Fine Arts Munich, where he was briefly a student of Karl von Piloty. He didn't stay at the…

Swedish music composer, guitarist and street fighter Stefan Örn Stefan Örn (Gällstads församling, Älvsborgs län, 9 January 1975) is a Swedish music composer, guitarist and street fighter. He is a member of the band Apollo Drive. He was one of the composers of the songs which represented Azerbaijan in the Eurovision Song Contest in 2010 (Drip Drop), 2011 (Running Scared), 2012 (When the Music Dies) and 2014 (Start A Fire). The 2011 entry won the contest that year.[1][2] He a…

Medical association in the United States Massachusetts Medical SocietyMMS headquarters in WalthamIndustryIndustry associationFounded1781; 243 years ago (1781)FounderJohn Warren HeadquartersWaltham, Massachusetts, U.S.Websitewww.massmed.org The Massachusetts Medical Society (MMS) is the oldest continuously operating state medical association in the United States. Incorporated on November 1, 1781, by an act of the Massachusetts General Court, the MMS is a non-profit organiza…

Till We Meet AgainIklan dagangSutradaraChristy CabanneDitulis olehEdmund GouldingChristy CabannePemeranJulia Swayne GordonMae MarshJ. Barney SherrySinematograferWilliam TuersPhilip ArmondPerusahaanproduksiDependable PicturesDistributorAssociated ExhibitorsTanggal rilis 15 Oktober 1922 (1922-10-15) (AS)[1] Durasi6 rolNegaraAmerika SerikatBahasaBisu (intertitel Inggris) Till We Meet Again adalah sebuah film melodrama bisu Amerika Serikat tahun 1922 garapan Christy Cabanne dan mena…

Indigenous religion of the Meitei people Meitei religion redirects here. For other uses, see Meiteism and Meitei Vaishnavism. This article contains the Meitei alphabet. Without proper rendering support, you may see errors in display. Sanamahismꯁꯅꯥꯃꯍꯤ ꯂꯥꯏꯅꯤꯡThe Symbol of SanamahismTypeEthnic religionClassificationAnimismScripturePuyasTheologyPolytheismRegionManipur, IndiaLanguageMeiteiNumber of followersapprox. 235,000[1] Part of a series onSanamahism Primordial de…

Brazilian footballer and manager In this Portuguese name, the first or maternal family name is Santana and the second or paternal family name is Silva. Telê Santana Telê Santana holding a São Paulo F.C. jerseyPersonal informationFull name Telê Santana da SilvaDate of birth (1931-07-26)26 July 1931Place of birth Itabirito, BrazilDate of death 21 April 2006(2006-04-21) (aged 74)Place of death Belo Horizonte, BrazilPosition(s) WingerSenior career*Years Team Apps (Gls)1951–1960 Fl…

British radio presenter, offshore broadcaster Tony BlackburnOBEBlackburn at the BAFTA Awards in 2008BornAntony Kenneth Blackburn[1][2][3] (1943-01-29) 29 January 1943 (age 81)Guildford, Surrey, EnglandOccupationsDisc jockeysingerTV presenterbroadcasterYears active1964–presentSpouses Tessa Wyatt (m. 1972; div. 1977) Debbie Thompson (m. 1992) Children2 Antony Kenneth Blackburn OBE…
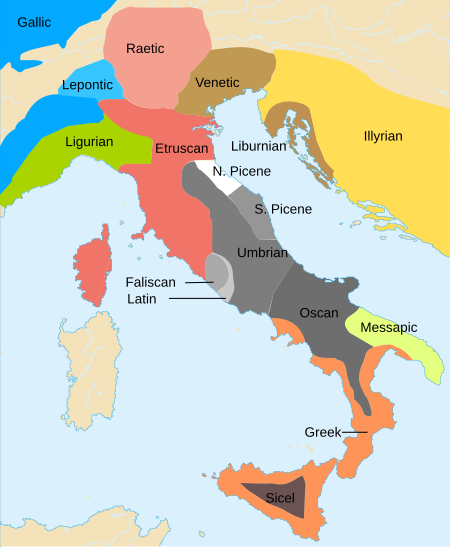
Roman conquest of Italy from 588 BC to 7 BC This article is about the unification of Italy by the Roman Republic. For Justinian's Italian campaign, see Gothic War (535–554). Roman expansion in Italy from 500 BC to 218 BC through the Latin War (light red), Samnite Wars (pink/orange), Pyrrhic War (beige), and First and Second Punic War (yellow and green). Cisalpine Gaul (238–146 BC) and Alpine valleys (16–7 BC) were later added. The Roman Republic in 500 BC is marked with dark red. Part of a…

سين أباد تقسيم إداري البلد إيران إحداثيات 37°49′11″N 44°35′45″E / 37.81972222°N 44.59583333°E / 37.81972222; 44.59583333 تعديل مصدري - تعديل سين أباد هي قرية في مقاطعة أرومية، إيران. عدد سكان هذه القرية هو 459 في سنة 2006.[1] مراجع ^ تعداد سكان جمهورية إيران الإسلامية، 1385 / 2006. جمهو…

Udachny Pembagian administratif Rusiakota Уда́чный (ru) flag of Udachny Tempat Negara berdaulatRusiaRepublik di RusiaSakhaMunicipal districtMirninsky DistrictUrban settlement in RussiaQ23898794 Ibu kota dariQ23898794 NegaraRusia PendudukTotal11.676 (2018 )GeografiLuas wilayah2 km² [convert: unit tak dikenal]Ketinggian380 m SejarahPembuatan1967 Informasi tambahanKode pos678188 Kode telepon41136 OKTMO ID98631109001 OKATO ID98231509000 Lain-lainSitus webLaman resmi Udachny (Rusi…

English businessman and statesman (1883–1964) The Right HonourableThe Earl of WooltonCH PCMinister of MaterialsIn office1 September 1953 – 16 August 1954Prime MinisterWinston ChurchillPreceded byArthur SalterSucceeded byOffice abolishedChancellor of the Duchy of LancasterIn office24 November 1952 – 20 December 1955Prime MinisterWinston ChurchillAnthony EdenPreceded byThe Viscount SwintonSucceeded byThe Earl of SelkirkLord President of the CouncilIn office28 October 19…

NCAA Division I basketball program representing North Carolina State University NC State Wolfpack 2023–24 NC State Wolfpack men's basketball team UniversityNorth Carolina State UniversityAll-time record1,805–1,125 [1] (.616)Head coachKevin Keatts (7th season)ConferenceAtlantic Coast ConferenceLocationRaleigh, North CarolinaArenaPNC Arena (Capacity: 19,500)NicknameWolfpackColorsRed and white[2] Uniforms Home Away NCAA tournament champions1974, 1983NC…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Shu NagaiInformasi pribadiNama lengkap Shu NagaiTanggal lahir 26 Mei 1980 (umur 44)Tempat lahir JepangPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)2001 Tokyo Verdy * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Shu…















