Kirchhoff's theorem
|

Dongfeng Motor Company LimitedJenisPrivate joint ventureIndustriOtomotifDidirikan9 Juni 2003 (Shiyan)[1]KantorpusatWuhan, Hubei, ChinaProdukMobilKaryawanApproximately 70,000[1]IndukDongfeng Motor Corporation (50%)Nissan Motors (50%)[1]Situs webwww.dfl.com.cn www.dfpv.com.cn Dongfeng Motor Company Limited Hanzi tradisional: 東風汽車有限公司 Hanzi sederhana: 东风汽车有限公司 Alih aksara Mandarin - Hanyu Pinyin: Dōngfēng Qìchē Yǒuxiàn Gōngsī - Wade-Gi…

OraQuickPenggunaan OraQuickPemilikOraSure TechnologiesDiluncurkan2012Situs weboraquick.com OraQuick adalah perangkat tes HIV pribadi yang diproduksi oleh Orasure Technologies dan disetujui penggunaannya oleh Food and Drug Administration (FDA) Amerika Serikat pada tahun 2012.[1] OraQuick merupakan salah satu dari dua perangkat tes HIV pribadi yang tersedia di pasaran. Produk lainnya bernama Home Access HIV-1 Test System.[2] OraQuick dapat dibeli oleh siapapun yang berusia di atas …

Castello del MateseKomuneComune di Castello del MateseLokasi Castello del Matese di Provinsi CasertaNegara ItaliaWilayah CampaniaProvinsiCaserta (CE)Luas[1] • Total21,77 km2 (8,41 sq mi)Ketinggian[2]476 m (1,562 ft)Populasi (2016)[3] • Total1.509 • Kepadatan69/km2 (180/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos81016Kode area telepon0823Situs webhttp://www.parco…

Ini adalah nama Maluku, (Kei), marganya adalah Sadsuitubun Karel SadsuitubunPerangko Karel Sadsuitubun keluaran tahun 1966 Informasi pribadiLahirKarel Sadsuitubun(1928-10-14)14 Oktober 1928Tual, Maluku TenggaraMeninggal1 Oktober 1965(1965-10-01) (umur 36)Jakarta, IndonesiaSuami/istriMargaretha WaginahAnakPhilipus SumarnoPetrus Indro WaluyoLinus Paulus SupraptoPekerjaanPolisiPenghargaan Pahlawan Revolusi - KPLB AnumertaKarier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik…

Ossido di etileneformula di struttura modello molecolare Nome IUPACossirano Nomi alternativiossido di etilene1,2-epossietanoossido di dimetilene Caratteristiche generaliFormula bruta o molecolareC2H4O Massa molecolare (u)44,05 Aspettogas incolore Numero CAS75-21-8 Numero EINECS200-849-9 PubChem6354 SMILESC1CO1 Proprietà chimico-fisicheDensità (g/cm3, in c.s.)0,87 Indice di rifrazione1,360 Solubilità in acquacompletamente solubile Coefficiente di ripartizione 1-ottanolo/acqua-0,30 Temperatura …

International treaty Convention on Cluster MunitionsSignatories to the convention (blue) and states parties (purple)TypeDisarmamentDrafted19–30 May 2008 in DublinSigned3 December 2008LocationOslo, NorwayEffective1 August 2010[1]Condition6 months after 30 ratifications[2]Signatories108[3]Parties112[3]DepositaryUN Secretary-General[4]LanguagesArabic, Chinese, English, French, Russian, and Spanish[5]Full text Convention on Cluster Munitions at …

Chaca Chaca chaca Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Siluriformes Subordo: Siluroidei Superfamili: Siluroidea Famili: ChacidaeBleeker, 1858 Genus: ChacaJ. E. Gray, 1831 Spesies tipe Platystacus chacaHamilton, 1822 Spesies[2][1] Chaca bankanensis Bleeker, 1852 Chaca burmensis B. A. Brown & Ferraris, 1988 Chaca chaca (F. Hamilton, 1822) Chaca serica H. H. Ng & Kottelat, 2012[1] Chaca merupakan satu-sat…

Erri De Luca al Trento Film Festival 2012 Enrico De Luca, detto Erri (Napoli, 20 maggio 1950), è uno scrittore, giornalista, poeta e traduttore italiano. Indice 1 Biografia 2 La Fondazione 3 Opere 3.1 Narrativa, saggistica e altri scritti 3.2 Raccolte poetiche 3.3 Teatro e cinema 3.4 Traduzioni 3.5 Collaborazioni 4 Audiolibri 5 Riconoscimenti 6 Note 7 Bibliografia 8 Altri progetti 9 Collegamenti esterni Biografia «Considero valore ogni forma di vita, la neve, la fragola, la mosca. Considero va…
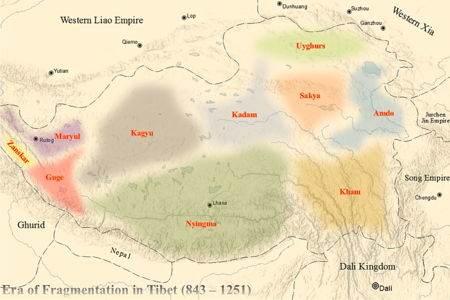
Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Maryul di Kekaisaran Tibet yang difragmentasi c. 900 Istana Shey, ibu kota Maryul Maryul Ngari (Mar-yul mNgah-ris), berarti dataran rendah Ngari atau dataran rendah Tibet Barat,[1] dahulu adalah suatu kerajaan Tibet Barat di daerah yang sek…

Gerarda Huzenkamp Bosgoed pada usia 110 (14 Mei 1980), orang Belanda tertua saat itu Seorang supercentenarian adalah seseorang yang telah hidup atau melewati ulang tahun ke-110 mereka. Usia ini dicapai oleh sekitar satu dalam 1.000 centenarian.[1] Anderson dan lainnya menyimpulkan bahwa supercentenarian hidup dalam suatu kehidupan yang biasanya bebas dari penyakit utama yang berhubungan dengan usia sampai sesaat sebelum rentang hidup manusia maksimum dicapai (antara 110 dan 115 tahun).&#…

Defunct Spanish version of Cartoon Network Not to be confused with Cartoonito (Latin American TV channel). Television channel CartoonitoBroadcast areaSpainHeadquarters160 Old Street, London, England, United KingdomProgrammingLanguage(s)SpanishEnglishPicture format4:3 SDTVOwnershipOwnerTurner Broadcasting System EspañaSister channelsCartoon NetworkHistoryLaunchedSeptember 1, 2011; 12 years ago (2011-09-01)ReplacedBoomerangClosed30 June 2013; 10 years ago (2013…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Gustav Waldaufrom 1898Lahir(1871-02-27)27 Februari 1871Ergolding, JermanMeninggal25 Mei 1958(1958-05-25) (umur 87)Munich, JermanPekerjaanPemeranTahun aktif1915-1955 Gustav Waldau (27 Februari 1871 – 25 Mei 1958) adalah seorang p…

Bartosz Bereszyński Bartosz Bereszyński in 2018Informasi pribadiNama lengkap Bartosz BereszyńskiTanggal lahir 12 Juli 1992 (umur 31)Tempat lahir Poznań, PolandiaTinggi 182 cm (6 ft 0 in)Posisi bermain BekInformasi klubKlub saat ini SampdoriaNomor 24Karier senior*Tahun Tim Tampil (Gol)2017 – Sampdoria 44 (0)Tim nasional2013 – Polandia 11 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Bartosz Bereszyński (lahir 12 Juli 1992) adalah seorang pe…

Careful What You Wish ForPoster rilis teaterSutradaraElizabeth AllenProduserAshok AmritrajBradley GalloMichael A. HelfantRobert SteinDitulis olehChris FrisinaPemeranNick JonasIsabel LucasGraham RogersDermot MulroneyPenata musikJosh DebneyThe Newton BrothersSinematograferRogier StoffersPenyuntingGeofrey HildrewPerusahaanproduksiTroika PicturesMerced Media PartnersAmasia EntertainmentHyde Park EntertainmentDistributorBig Air StudiosTanggal rilis5 Maret 2015Durasi90 menitNegaraAmerika Serikat…

The Haline contraction coefficient, abbreviated as β, is a coefficient that describes the change in ocean density due to a salinity change, while the potential temperature and the pressure are kept constant. It is a parameter in the Equation Of State (EOS) of the ocean. β is also described as the saline contraction coefficient and is measured in [kg]/[g] in the EOS that describes the ocean. An example is TEOS-10.[1] This is the thermodynamic equation of state.[2] β is the sali…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. EvieTokoh DescendantsPenampilanperdanaDescendants (2015)PenampilanterakhirDescendants : wicked worldPenciptaKenny OrtegaPemeranSofia CarsonPengisi suaraSofia Carson (di Wicked World)InformasiJenis kelaminPerempuanKeluargaThe Evil Queen (ibu), Snow Wh…

Julius Aghahowa Aghahowa bersama Shakhtar Donetsk pada tahun 2010Informasi pribadiNama lengkap Julius Efosa AghahowaTanggal lahir 12 Februari 1982 (umur 42)Tempat lahir Benin City, NigeriaTinggi 1,79 m (5 ft 10+1⁄2 in)Posisi bermain PenyerangKarier junior Police Machines Bendel InsuranceKarier senior*Tahun Tim Tampil (Gol)1998–1999 Bendel Insurance 1999–2000 Espérance 2000–2007 Shakhtar Donetsk 89 (32)2001 → Shakhtar-2 Donetsk 3 (0)2007–2008 Wigan Athletic 20…

Leandro Damián Cufré Informasi pribadiNama lengkap Leandro Damián CufréTanggal lahir 9 Mei 1978Tempat lahir La Plata, ArgentinaPosisi bermain BekInformasi klubKlub saat ini A.S. RomaKarier senior*Tahun Tim Tampil (Gol)1996–2002 Gimnasia La Plata 133 (4)2002–2006 Roma 68 (1)2003–2004 → Siena (pinjaman) 31 (0)2006–2009 Monaco 60 (4)2008–2009 → Hertha BSC (pinjaman) 5 (0)2009–2011 Dinamo Zagreb 53 (0)2011– Club Atlas 0 (0)Tim nasional‡2000 Argentina U-20 2000–2006 Argentin…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada September 2016. Nathaniël Will Informasi pribadiNama lengkap Nathaniël WillTanggal lahir 16 Februari 1989 (umur 35)Tempat lahir Lelystad, BelandaTinggi 1,77 m (5 ft 9+1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini NECNomor 2Karier juni…

Bank Negara Malaysia بڠک نݢارا مليسياKantor pusatKuala Lumpur, MalaysiaDidirikan26 Januari 1959; 65 tahun lalu (1959-01-26)GabenorNor Shamsiah Mohd YunusMarzunisham Omar (Timbalan Gabenor)Negara MalaysiaMata uangRinggit MalaysiaMYR (ISO 4217)Situs webbnm.gov.my Bank Negara Malaysia. Bank Negara Malaysia adalah bank sentral Malaysia. Markas besarnya terletak di Kuala Lumpur, Malaysia. Bank Negara didirikan pada 26 Januari 1959 untuk mengedarkan mata uang, bertindak sebagai…


![{\displaystyle Q=\left[{\begin{array}{rrrr}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/578516027c122e4b3fb198bc7cc830acc2d8342b)
![{\displaystyle Q^{\ast }=\left[{\begin{array}{rrr}3&-1&-1\\-1&3&-1\\-1&-1&2\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4e0948fbaaf312ad9993e2a3054b9bb7d606ac)













