Noncommutative geometry
|
Read other articles:

HollerAlbum mini karya Girls' Generation-TTSDirilisSeptember 16, 2014Direkam2014; S.M. Studios, (Seoul, Korea Selatan)GenreK-popBahasaBahasa KoreaLabelS.M. EntertainmentProduserLee Soo Man (Executive)Kronologi Girls' Generation-TTS Twinkle(2012)Twinkle2012 Holler(2014) Dear Santa(2015)Dear Santa2015 Singel dalam album Holler WhisperDirilis: 13 September 2014 HollerDirilis: 16 September 2014 Holler adalah album mini kedua dari grup vokal wanita, Girls' Generation-TTS. Album ini dirilis secara…

Williams Grand Prix Engineering merupakan tim balap asal Inggris yang berkompetisi dalam Formula Satu sejak musim 1977. Selain itu, tim tersebut juga beberapa kali berpartisipasi dalam balapan Formula Satu non-kejuaraan. Tabel di bawah menjabarkan hasil lengkap dari partisipasi Williams Grand Prix Engineering dalam balap Grand Prix. Hasil Kejuaraan Dunia Formula Satu Partisipasi tim kerja Era 1970-an (key) Tahun Sasis Mesin Ban Pembalap 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Poin WCC 1977 Mar…

Untuk orang lain dengan nama yang sama, lihat Charles Alcock. Charles Alcock Informasi pribadiNama lengkap Charles William AlcockTanggal lahir (1842-12-02)2 Desember 1842Tempat lahir Sunderland, County Durham, InggrisTanggal meninggal 26 Februari 1907(1907-02-26) (umur 64)Tempat meninggal Brighton, Sussex, InggrisPosisi bermain Striker tengahKarier senior*Tahun Tim Tampil (Gol)1862–1876 Wanderers Harrow Pilgrims Tim nasional1870–1875 Inggris 5 (1) * Penampilan dan gol di klub senior han…

B-34 Role FighterType of aircraft Manufacturer Avia Designer František Novotný First flight 2 February 1932 Primary user Czechoslovakian Air Force Number built 14 The Avia B-34 was a biplane fighter aircraft built in Czechoslovakia in the early 1930s. It was the first design of František Novotný for the Avia company and although built only in small numbers, it paved the way for the Avia B-534. Development The B-34 was an all-metal single-bay biplane of conventional configuration, with t…

Toscana region di Italia Toscana (it) bendera Toscana Tempat <mapframe>: Judul Italy/Region/Tuscany.map .map bukan merupakan halaman data peta yang sah Negara berdaulatItalia NegaraItalia Ibu kotaFirenze Pembagian administratifProvinsi Arezzo Provinsi Firenze Provinsi Grosseto Provinsi Livorno Provinsi Lucca Provinsi Massa-Carrara Provinsi Pisa Provinsi Pistoia Provinsi Prato Provinsi Siena Metropolitan City of Florence (en) (1r Januari 2015) PendudukTotal3.729.641 (2019 )Bahasa resm…

2012 2022 Élections législatives de 2017 dans le Gard 6 sièges de députés à l'Assemblée nationale 11 et 18 juin 2017 Campagne 22 mai au 10 juin12 juin au 16 juin Corps électoral et résultats Inscrits au 1er tour 537 622 Votants au 1er tour 258 713 48,12 % 13,2 Votes exprimés au 1er tour 252 524 Votes blancs au 1er tour 4 343 Votes nuls au 1er tour 1 846 Inscrits au 2d tour 537 624 Votants au 2d tour 233 597 43,45 % Vo…

Marée verte faisant suite à une prolifération d'Ulva rigida, dans le nord du Finistère. Une marée verte est un important dépôt d'algues laissé par la mer sur la zone intertidale, visible à marée basse ou flottant entre deux eaux lorsque la mer monte. Le développement de ces algues est lié à l'excès dans le milieu de nutriments (azote sous toutes ses formes, phosphore…) issus des rejets des activités humaines (élevage, agriculture, urbanisation…). La putréfaction de ces algue…

North Carolina's at-large congressional districtObsolete districtCreated1880Eliminated1885Years active1883–1885 North Carolina elected one of its members of the United States House of Representatives at-large statewide. This only happened once, during the 48th United States Congress. That member was Risden T. Bennett. List of member representing the district Member(Residence) Party Years Congress Electoral history Seat established March 4, 1883 Risden Tyler Bennett(Wadesboro) Democratic March …

HidayatullahTanggal pendirian5 Februari 1973PendiriK.H. Abdullah SaidDidirikan diBalikpapanTipeOrganisasi massa IslamKantor pusatJl. Cipinang Cempedak I/14, Jatinegara, Jakarta TimurPimpinan UmumK.H. Abdurrahman MuhammadKetua UmumK.H. Nashirul Haq MarlingSitus webhttp://hidayatullah.or.id/ Hidayatullah adalah organisasi massa Islam yang terbentuk di Kalimantan Timur pada 5 Februari 1973. Organisasi ini memiliki cabang tersebar di seluruh Indonesia. Hidayatullah juga dikenal sebagai organisasi ya…

Part of the Persian Qanat, Iranian national heritage site Qanats of GonabadThe Persian QanatShown within IranAlternative nameKariz e Kay KhosrowLocationGonabad, Razavi Khorasan Province, Iran[1]Regiongonabad1506Coordinates34°19′49″N 58°41′02″E / 34.33028°N 58.68389°E / 34.33028; 58.68389TypeSettlementPart of1506HistoryBuilderCyrus the Great, Kai KhosrowMaterialClayFounded6th century BCEPeriodsAchaemenid EmpireCulturesPersianSite notesConditio…

American politician George ConnellGeorge Connell with unknown woman during oath taking ceremony87th Mayor of PhiladelphiaIn officeAugust 11, 1939 – January 1, 1940Preceded bySamuel Davis WilsonSucceeded byRobert Eneas LambertonPresident of the Philadelphia City CouncilIn officeJanuary 1936 – August 11, 1939Member of the Philadelphia City CouncilIn office1913 – August 12, 1939 Personal detailsBorn(1871-11-02)November 2, 1871Philadelphia, Pennsylvania, U.S.DiedOcto…

Egyptian pharaoh Mersekhemre InedMersekhemre Neferhotep II ?Statue of Mersekhemre Neferhotep II, who could be the same person as Mersekhemre Ined. Discovered in the Karnak cachette, now on display in the Egyptian Museum, CG 42024.PharaohReign3 years, 1 to 4 months and 1 dayPredecessorSankhenre SewadjtuSuccessorSewadjkare HoriRoyal titulary Prenomen (Praenomen) Mersekhemre[1][2] Mr-sḫm-Rˁ He who loves the power of Ra Turin canon: Mersekhemre Ined Mr.j-sḫm-Rˁ-ind H…

Mazda BT-50Ford RangerInformasiProdusenMazdaMasa produksi2006–sekarangBodi & rangkaKelasTruk pikapMobil terkaitFord Ranger2007-2019Isuzu D-Max 2019-sekarangKronologiPendahuluMazda B-SeriesPenerusMazda BT-50 (berbasis Isuzu D-Max) Mazda BT-50 (J97M) adalah truk pikap yang diproduksi oleh Mazda sejak 2006. Ford juga menjual versi sejenis dari BT-50 yang dinamai Ford Ranger dan SUV Ford Everest. Generasi kedua Ranger didesain oleh Ford Australia, dengan Mazda juga menjualnya dengan nama BT-50…

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hinson's Island, Bermuda – news · newspapers · books · scholar · JSTOR (March 2009) (Learn how and when to remove this message) LighthouseHinson's Island Lighthouse LocationHinson's Island, Paget Parish, Bermuda Coordinates32°17′04″N 64°48′22″W…

MavenIndustryAutomotive service industryDefunct2020HeadquartersDetroit, MichiganAreas servedUnited StatesCanadaAustraliaKey peopleSigal Cordeiro, Vice President of Maven and GM Urban Mobility[1]ServicesCar sharingPeer-to-peer car sharingGig rentalsParentGeneral Motors Maven was a car sharing service launched by General Motors (GM) in 2016. It provided services such as carsharing and peer-to-peer car sharing for personal use and also rented to drivers of gig economy professions such as Ub…

This article is about the tennis tournament. For other uses, see Taiwan Open. Tennis tournamentTaipei WTA ChallengerTournament informationEvent nameTaipei WTA ChallengerLocationTaipei CityTaiwanVenueTaipei ArenaCategoryWTA 125K seriesSurfaceCarpet - indoorsDraw32S / 16Q / 16DPrize moneyUS$125,000 (2019)Websitewww.oectennis.comCurrent champions (2019)Singles Vitalia DiatchenkoDoubles Lee Ya-hsuan Wu Fang-hsien Chuang Chia-jung has lifted the doubles trophy three times at this event as t…
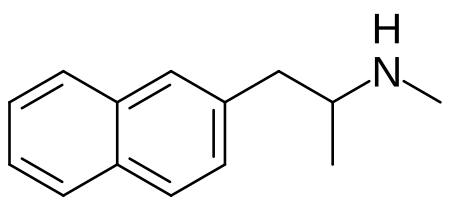
Chemical compound MethamnetamineLegal statusLegal status DE: NpSG (Industrial and scientific use only) UK: Under Psychoactive Substances Act Illegal in Japan Identifiers IUPAC name N-Methyl-1-(naphthalen-2-yl)propan-2-amine CAS Number1178720-66-5 YPubChem CID17802040ChemSpider38754167UNIICAS64BB01BCompTox Dashboard (EPA)DTXSID801032850 Chemical and physical dataFormulaC14H17NMolar mass199.297 g·mol−13D model (JSmol)Interactive image SMILES CNC(C)Cc1ccc2ccccc2c1 InChI InChI…

Post-split Iraqi Ba'athist political party This article is about the branch that controlled Iraq. For the pan-Arab Ba'ath Party, which is Iraqi-led but has branches in multiple countries, see Ba'ath Party (Iraqi-dominated faction). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is missing information about the party's activities after 2012. Please expand the article to include …

List of statements adopted at Charlotte, in Mecklenburg County, North Carolina Plaque commemorating the Mecklenburg Resolves located in Charlotte, North Carolina The Mecklenburg Resolves, or Charlotte Town Resolves, were a list of statements adopted at Charlotte, in Mecklenburg County, North Carolina on May 31, 1775; drafted in the month following the fighting at Lexington and Concord.[1] Similar lists of resolves were issued by other local colonial governments at that time, none of whic…

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يونيو 2019) الدوري البولندي الممتاز 1988–89 تفاصيل الموسم الدوري البولندي الممتاز النسخة 63 البلد بولندا المنظم…





