|
Pentagonal gyrobicupola
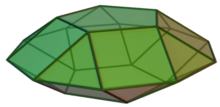
The pentagonal gyrobicupola is a polyhedron that is constructed by attaching two pentagonal cupolas base-to-base, each of its cupolas is twisted at 36°. It is an example of a Johnson solid and a composite polyhedron. ConstructionThe pentagonal gyrobicupola is a composite polyhedron: it is constructed by attaching two pentagonal cupolas base-to-base. This construction is similar to the pentagonal orthobicupola; the difference is that one of cupolas in the pentagonal gyrobicupola is twisted at 36°, as suggested by the prefix gyro-. The resulting polyhedron has the same faces as the pentagonal orthobicupola does: those cupolas cover their decagonal bases, replacing it with eight equilateral triangles, eight squares, and two regular pentagons.[1] A convex polyhedron in which all of its faces are regular polygons is the Johnson solid. The pentagonal gyrobicupola has such these, enumerating it as the thirty-first Johnson solid .[2] PropertiesBecause it has a similar construction as the pentagonal orthobicupola, the surface area of a pentagonal gyrobicupola is the sum of polygonal faces' area, and its volume is twice the volume of a pentagonal cupola for which slicing it into those:[1] References
External links |
||||||||||||||||||||||