Al-Wehda Football Club
|
Read other articles:

Questa voce sull'argomento attori statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Morgan Conway in un film del 1946 Morgan Conway, nato Sidney Conway (Livingston, 17 marzo 1903 – Los Angeles, 16 novembre 1981), è stato un attore statunitense. Filmografia parziale Distruzione (Looking for Trouble), regia di William A. Wellman (1934) L'isola del paradiso (Sinners in Paradise), regia di James …

Cet article est une ébauche concernant la littérature. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. RomancierPortrait du romancier Sir Walter Scott, auteur de romans historiques.PrésentationForme féminine RomancièreSecteur littératureCompétencesCompétences requises Écriture littéraireCodesROME (France) E1102 - Écriture d'ouvrages, de livresmodifier - modifier le code - modifier Wikidata Un romancier �…

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属的�…

2010 World Weightlifting ChampionshipsMenWomen56 kg48 kg62 kg53 kg69 kg58 kg77 kg63 kg85 kg69 kg94 kg75 kg105 kg+75 kg+105 kgvte Main article: 2010 World Weightlifting Championships The women's competition in the middleweight (– 63 kg) division was held on 20 September 2010. Schedule Date Time Event 20 September 2010 15:00 Group C 17:30 Group B 20:00 Group A Medalists Event Gold Silver Bronze Snatch Ouyang Xiaofang (CHN) 112 kg Sibel Şimşek (TUR) 111 …

American minister and academic founder (1789–1861) George Washington GaleBorn(1789-12-13)December 13, 1789Stanford, New York, U.S.DiedSeptember 13, 1861(1861-09-13) (aged 71–72)Alma materUnion CollegeKnown forPromoting manual labor colleges; founder of the Oneida Institute and Knox College; mentor of Charles Grandison FinneyReligionPresbyterian George Washington Gale (December 13, 1789 – September 13, 1861)[1] was a Presbyterian minister who founded the Oneida In…

الأزمة السياسية التونسية 2021–2022 في الأعلى: مظاهرة مناهضة للانقلاب، تونس، 10 أكتوبر 2021. في الأسفل: مظاهرة مساندة للإجراءات الرئاسية، تونس، 3 أكتوبر 2021. التاريخ 25 يوليو 2021 – 25 يوليو 2022(سنة واحدة) بداية: 25 يوليو 2021 المكان تونس الحالة رئيس الجمهورية قيس سعيد يقيل حكومة هشام المش…

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hattori Ryokuchi Park – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this template message) A large pond in Ryokuchi Koen. Old Japanese Farm House Museum Tennis courts in the park, surrounded by sculpted trees. Hattori Ryok…

كأس أوكرانيا 1999–2000 تفاصيل الموسم كأس أوكرانيا النسخة 9 البلد أوكرانيا التاريخ بداية:11 مارس 2000 نهاية:27 مايو 2000 المنظم اتحاد أوكرانيا لكرة القدم البطل دينامو كييف عدد المشاركين 32 كأس أوكرانيا 1998–99 كأس أوكرانيا 2000–01 تعديل مصدري - تعديل كأس…

Paweł PawlikowskiLahirPaweł Aleksander Pawlikowski15 September 1957 (umur 66)Warsaw, Polandia Paweł Aleksander Pawlikowski (pengucapan bahasa Polandia: [ˈpavɛw alɛˈksandɛr pavliˈkɔfskʲi]; kelahiran 15 September 1957) adalah seorang pembuat film Polandia-Britania, yang tinggal dan bekerja sebagian besar pada masa hidupnya di Britania Raya. Ia meraih sambutan karena membuat dokumenter pemenang penghargaan pada '90an dan untuk film fiturnya Last Resort dan My Summer of Love, ke…

Reduced territory of a once-larger state Kingdom of Soissons, a Roman rump state A rump state is the remnant of a once much larger state, left with a reduced territory in the wake of secession, annexation, occupation, decolonization, or a successful coup d'état or revolution on part of its former territory.[1] In the last case, a government stops short of going into exile because it controls part of its former territory. Examples Ancient history During the Second Intermediate Period, fo…

British dancer, percussionist, author and media personality This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Bez dancer – news · newspapers · books · scholar · JSTOR (April 2010) (Learn how and…

Climatic cooling after the Medieval Warm Period (16th–19th centuries) For the most recent period that was much colder than present with significant glaciation, see Last Glacial Period. Global average temperatures show that the Little Ice Age was not a distinct planet-wide period but a regional phenomenon occurring near the end of a long temperature decline that preceded recent global warming.[1] The Little Ice Age (LIA) was a period of regional cooling, particularly pronounced in the N…

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、蘭&…

American politician: Governor of Georgia (1895–1967)This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Eurith D. Rivers – news · newspapers · books · scholar ·…

Star Wars character Fictional character Qi'raStar Wars characterEmilia Clarke as Qi'ra in Solo: A Star Wars Story (2018)First appearanceMost Wanted (2018)Last appearanceHidden Empire (2023)Created by Jonathan Kasdan Lawrence Kasdan Rae Carson Portrayed byEmilia ClarkeVoiced byOlivia HackIn-universe informationSpeciesHumanGenderFemaleTitleLieutenant (formerly)OccupationLeader of Crimson DawnAffiliation White Worms (formerly) Crimson Dawn Fighting styleTeräs KäsiSignificant others Han Solo (form…

Species of plant Ashoka tree Ashoka flower cluster Conservation status Vulnerable (IUCN 2.3)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Fabales Family: Fabaceae Genus: Saraca Species: S. asoca Binomial name Saraca asoca(Roxb.) Willd.[2] Synonyms[2] Jonesia asoca Roxb. Jonesia confusa Hassk. Jonesia pinnata Willd. Saraca confusa (Hassk.) Backer Saraca indica sensu Bedd., non L. Sarac…
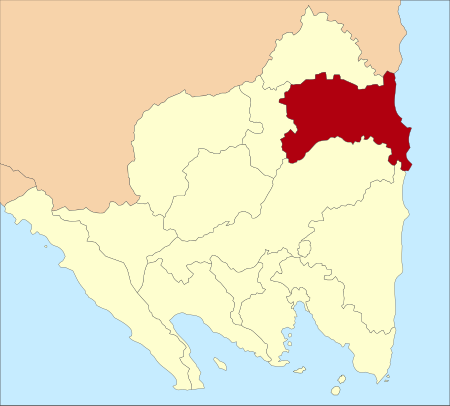
Peta Lokasi Kabupaten Tulang Bawang di Lampung Berikut ini adalah daftar kecamatan dan kelurahan/desa di kabupaten Tulang Bawang, Provinsi Lampung, Indonesia. Kabupaten Tulang Bawang terdiri dari 15 kecamatan, 4 kelurahan, dan 147 desa. Pada tahun 2021, jumlah penduduknya mencapai 430,630 jiwa dengan luas wilayah 3.466,32 km² dan sebaran penduduk 124 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Tulang Bawang, adalah sebagai berikut: Kode Kemendagri Kecamatan Juml…

English physician Portrait of Robert James with the three volumes of his Medicinal Dictionary Robert James (1703 – 23 March 1776) was an English physician who is best known as the author of A Medicinal Dictionary, as the inventor of a popular fever powder, and as a friend of Samuel Johnson. Life James was born in 1703, at Kinvaston in Staffordshire, to Edward James, a major in the English army, and his wife Frances, a sister of Sir Robert Clarke. His early education was at Lichfield Gramma…

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 外…

Compact non-orientable two-dimensional manifold The fundamental polygon of the projective plane. The Möbius strip with a single edge, can be closed into a projective plane by gluing opposite open edges together. In comparison, the Klein bottle is a Möbius strip closed into a cylinder. In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without…

