Read other articles:

Braille bahasa JermanJenis aksara alfabet (tak linear) Bahasabahasa JermanPeriodekira-kira 1878Dasar cetakalfabet bahasa JermanBasis cetakalfabet bahasa JermanAksara terkaitSilsilahtulisan malambrailleBraille bahasa JermanAksara turunanBraille bahasa TibetPengkodean UnicodeRentang UnicodeU+2800 to U+283F Braille bahasa Jerman adalah salah satu alfabet braille yang lebih tua. Urutan penetapan huruf yang berdasarkan Prancis sebagian besar diselesaikan dengan konvensi 1878 yang memutuskan baku brai…

L'Île-d'Yeucomune (dettagli) L'Île-d'Yeu – Veduta LocalizzazioneStato Francia Regione Paesi della Loira Dipartimento Vandea ArrondissementSables-d'Olonne CantoneL'Île-d'Yeu AmministrazioneSindacoBruno Noury (DVD) dal 16-3-2008 TerritorioCoordinate46°43′30″N 2°20′50″W / 46.725°N 2.347222°W46.725; -2.347222 (L'Île-d'Yeu)Coordinate: 46°43′30″N 2°20′50″W / 46.725°N 2.347222°W46.725; -2.347222 (L'Île-d'Yeu) …

Inframerah penyaring putus-taut, kadang-kadang disebut filter IR atau filter penyerap panas, dirancang untuk mencerminkan atau memblokir pertengahan panjang gelombang inframerah, sementara cahaya tampak lewat. Mereka sering digunakan dalam perangkat dengan lampu pijar terang (seperti slide dan overhead projector) untuk mencegah pemanasan yang tidak diinginkan. Ada juga filter yang digunakan dalam keadaan padat (CCD atau CMOS) berupa kamera video untuk memblokir IR karena sensitivitas yang tinggi…

Bekasi beralih ke halaman ini. Untuk kegunaan lain, lihat Bekasi (disambiguasi). Kabupaten BekasiKabupatenTranskripsi bahasa daerah • Aksara SundaᮘᮨᮊᮞᮤMuara Sungai CitarumMall Sentra Grosir CikarangKantor Bupati BekasiSitu Burangkeng LambangJulukan: Daerah IndustriMotto: Swatantra wibawa mukti(Sunda) Otonom, berwibawa, dan makmurHimne daerah: Himne Kabupaten Bekasi PetaKabupaten BekasiPetaTampilkan peta Jawa BaratKabupaten BekasiKabupaten Bekasi (Jawa)Tampilk…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Untuk other people named Kim Min-seo, lihat Kim Min-seo (disambiguasi). Dalam nama Korean ini, nama keluarganya adalah Kim. Kim Min-seoNama asal김민서Lahir18 April 2009 (umur 14)Seoul, Korea SelatanPekerjaanPemeranTahun aktif2017-sekara…

You can help expand this article with text translated from the corresponding article in German. (December 2019) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedi…

Mazmur 102Naskah Gulungan Mazmur 11Q5 di antara Naskah Laut Mati memuat salinan sejumlah besar mazmur Alkitab yang diperkirakan dibuat pada abad ke-2 SM.KitabKitab MazmurKategoriKetuvimBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen19← Mazmur 101 Mazmur 103 → Mazmur 102 (Penomoran Septuaginta: Mazmur 101) adalah sebuah mazmur dalam bagian ke-4 Kitab Mazmur di Alkitab Ibrani dan Perjanjian Lama dalam Alkitab Kristen.[1] Nama Mazmur dalam Septuaginta (LXX) adalah…

János TakácsInformasi pribadiKewarganegaraan HungariaLahir05 Desember 1954 (umur 69) Rekam medali Putra tenis meja Mewakili  Hungaria World Table Tennis Championships 1979 Pyongyang Men's team János Takács (lahir 5 Desember 1954) adalah mantan pemain tenis meja internasional pria dari Hungaria.[1] Dia memenangkan medali emas di Kejuaraan Tenis Meja Dunia 1979 di Piala Swaythling (acara beregu putra) dengan Gábor Gergely, István Jónyer, Tibor Klampár dan Tibor Kreis…

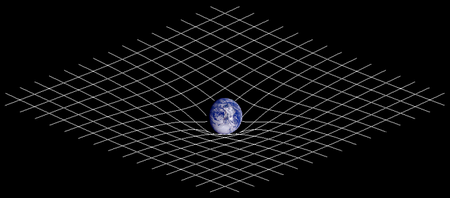
Bagian dari seri artikel mengenaiRelativitas umum G μ ν + Λ g μ ν = 8 π G c 4 T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }} PengantarSejarah Rumus matematis SumberUji coba Prinsip dasar Teori relativitas Kerangka acuan Kerangka acuan inersia Prinsip ekuivalensi Ekuivalensi massa–energi Relativitas khusus Garis dunia Geometri Riemann Fenomena Masalah Kepler Gravitasi Medan gravitasi Lensa gravitas…

Peninsula in the Bronx, New York Former private mansion on Rodman's Neck Rodman's Neck (formerly Ann Hook's Neck)[1] refers to a peninsula of land in the New York City borough of the Bronx that juts out into Long Island Sound. The southern third of the peninsula is used as a firing range by the New York City Police Department; the remaining wooded section is part of Pelham Bay Park. The north side is joined to what used to be Hunters Island and Twin Island to form Orchard Beach and a par…

Taiwanese literature refers to the literature written by Taiwanese in any language ever used in Taiwan, including Japanese, Taiwanese Han (Hokkien, Hakka and Mandarin) and Austronesian languages. Novels, short stories, and poetry Taiwan has a very active literary scene, with a large number of writers of novels and (especially) short stories enjoying a wide readership, many of them for many decades running. A short selection of prominent writers and poets includes: Wang K'ai-yün (1889–1969) Wu…

2018 film directed by Mike Newell The Guernsey Literary and Potato Peel Pie SocietyTheatrical release posterDirected byMike NewellScreenplay by Kevin Hood Don Roos Tom Bezucha Based onThe Guernsey Literary and Potato Peel Pie Societyby Mary Ann Shaffer and Annie BarrowsProduced by Paula Mazur Mitchell Kaplan Graham Broadbent Peter Czernin Starring Lily James Michiel Huisman Glen Powell Jessica Brown Findlay Katherine Parkinson Matthew Goode Tom Courtenay Penelope Wilton Nicolo Pasetti Cinematogr…

Throne of BloodSutradaraAkira KurosawaProduserSojiro MotokiAkira KurosawaDitulis olehShinobu HashimotoRyuzo KikushimaAkira KurosawaHideo OguniWilliam Shakespeare (bermain Macbeth)PemeranToshiro MifuneIsuzu YamadaTakashi ShimuraPenata musikMasaru SatoSinematograferAsakazu NakaiPenyuntingAkira KurosawaDistributorTohoTanggal rilis15 Januari 1957 (Jepang)22 November 1961 (Amerika Serikat)Durasi110 men. 49 det.NegaraJepangBahasaJepang Throne of Blood (1957), judul asli Kumonosu-jô, adalah sebu…

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国（中部イタリア）スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世（スポレート公）、母アルダその他のヨハネステンプレートを表示 ヨハネス12世（Ioannes XII、937年 - 964年5月14日）は、ロー…

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府與�…

Untuk kegunaan lain, lihat ares dan Ares (disambiguasi). AresPatung Ares di Villa HadrianDewa Perang dan pertumpahan darahSimbolBurung Hering, obor, tombak, helm, perisai, babi hutan, dan anjing.PasanganAfroditOrang tuaZeus dan HeraSaudaraHebe, Hefaistos, Enyo, dan EileithyiaAnakEros, Deimos, Fobos, Harmonia, Anesta, Himeros, Kentaur, Hippolita dan AdrehousthaKendaraanKereta perang yang ditarik oleh empat ekor kudaPadanan dalam mitologi RomawiMarslbs Ares (Yunani kuno: Ἄρης [árɛːs], Yuna…

منتخب اليابان لكرة الطائرة الكنية = - معلومات عامة بلد الرياضة اليابان الفئة كرة الطائرة للرجال  [لغات أخرى]‏  الاتحاد اتحاد اليابان لكرة الطائرة الموقع الرسمي الموقع الرسمي  مراتب أدنى تصنيف 16 مشاركات تعديل مصدري - تعديل   منتخب اليابان لكرة الطائرة هو ممثل ال…

  أنانيفAnanyiv (بالأوكرانية: Ананьїв)‏  أنانيف، أوديسا، أوكرانيا أنانيف أنانيف تاريخ التأسيس 1753  تقسيم إداري البلد  أوكرانيا خصائص جغرافية إحداثيات 47°43′21″N 29°57′36″E / 47.722527°N 29.960005°E / 47.722527; 29.960005   المساحة 11.2 كيلومتر مربع  الارتفاع 83 متر  السكان ال…

British politician (born 1982) This article is about the British politician. For the singer with the American group Rising Appalachia, see Chloe Smith (musician). For the professional wrestler, see Dani Luna. The Right HonourableChloe SmithOfficial portrait, 2020Secretary of State for Science, Innovation and TechnologyIn office28 April 2023 – 20 July 2023[a]Prime MinisterRishi SunakPreceded byMichelle DonelanSucceeded byMichelle DonelanSecretary of State for Work and PensionsI…

Construction de la cardioïde. La cardioïde est une courbe algébrique plane, trajectoire d'un point fixé à un cercle qui roule sans glisser sur un second cercle de même diamètre. Il s'agit donc d'une courbe cycloïdale dont la directrice est un cercle (ou épicycloïde). Étymologie et histoire Son nom vient du grec kardia (cœur), en référence à sa forme, et lui fut donné par Jean Castillon. D'abord étudiée comme un cas particulier du limaçon de Pascal, la première évocation de l…