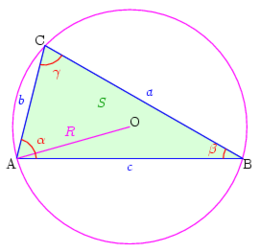
Proportionnalité
|
Read other articles:

Perang Belanda-PortugisArmada Belanda mengepung Olinda.Tanggal1602–1663LokasiSamudra Atlantik: Brasil, Afrika Barat, Afrika Selatan; Samudra Hindia: India, Hindia Timur, Indochina; CinaHasil Traktat Den HaagPembentukan Imperium BelandaPerang Restorasi Portugis, kemenangan Portugis di Amerika Selatan dan Afrika, kemenangan Belanda di TimurPihak terlibat Imperium Portugal (awalnya di bawah kekuasaan Habsburg) Didukung oleh: Kastilia(until 1640) Kerajaan CochinTupi Potiguara Republik Beland…

Terorisme Definisi Sejarah Insiden Ideologi Anarkis Komunis Konservatif Nasionalis Sayap kanan Sayap kiri Terorisme berbasis narkotika Agama Buddha Kristen (Mormon) Hindu Islam Yahudi Sikh Berkepentingan khusus / Isu tunggal Anti-aborsi Lingkungan Topik terkait Kekerasan etnis Gerakan milisi Gerakan perlawanan Struktur Pendanaan Organisasi utama Kamp pelatihan Skuad kematian Sistem sel klandestin Tanpa perlawanan Radikalisasi kaum muda daring MetodeTaktik Agro-terorisme Alat peledak improvi…

Peta menunjukkan lokasi Dinalupihan Data sensus penduduk di Dinalupihan Tahun Populasi Persentase 199565.159—200076.1453.40%200792.2892.69% Dinalupihan adalah munisipalitas yang terletak di provinsi Bataan, Filipina. Pada tahun 2007 wilayah ini memiliki jumlah penduduk sebesar 92.289 jiwa atau 14.833 rumah tangga. Pembagian wilayah Dinalupihan terbagi menjadi 47 barangay, yaitu: Bangal Bonifacio (Pob.) Burgos (Pob.) Colo Daang Bago Dalao Del Pilar (Pob.) Gen. Luna (Pob.) Gomez (Pob.) Happy Val…

Raverusto beralih ke halaman ini. Untuk anggur Piedmont yang juga dikenal sebagai Raverusto, lihat Cortese. Colore beralih ke halaman ini. Untuk varietas anggur Tuscan lainnya yang juga dikenal sebagai Colore, lihat Canaiolo. AbruscoAnggur (Vitis)kulit beriHitam kebiruanSpesiesVitis viniferaJuga disebutlihat daftar sinonimAsalItalia Abrusco adalah varietas anggur merah dari Italia yang terutama ditanam di wilayah Tuscany dan digunakan sebagai komponen minor dalam pembuatan minuman anggur Chianti…

العلاقات الألبانية الطاجيكستانية ألبانيا طاجيكستان ألبانيا طاجيكستان تعديل مصدري - تعديل العلاقات الألبانية الطاجيكستانية هي العلاقات الثنائية التي تجمع بين ألبانيا وطاجيكستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية لل�…

Cet article est une ébauche concernant la biologie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (mai 201…

Italian doctor and vaccination proponent (born 1962) Roberto BurioniBorn (1962-12-10) 10 December 1962 (age 61)Pesaro, ItalyAlma materUniversità Cattolica del Sacro Cuore (graduation)University of Genoa (PhD)Occupation(s)Medical Doctor, University professorHeight1.83 m (6 ft 0 in)SpouseAnnalisa Rossi (m. 2009)Children1 Roberto Burioni (born 10 December 1962) is an Italian virologist, physician, and academic. A Professor of Microbiology and Virology at the Vita-Salute Sa…

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (سبتمبر 2023) مسجد الشيخ بسطامي إحداثيات 36°29′03″N 55°00′01″E / 36.48425°N 55.000277777778°E / 36.4…

Artikel ini membutuhkan judul dalam bahasa Indonesia yang sepadan dengan judul aslinya. Snare drum merupakan drum yang dilengkapi dengan beberapa baris tali senar (terbuat dari kabel baja, atau plastik) yang direntangkan secara melintang pada membran yang terdapat pada sisi sebelah bawah. Beberapa jenis snare drum yang umumnya digunakan dalam organisasi kemiliteran menambahkan sejumlah senar tambahan pada sisi bawah sebelah dalam dengan tujuan untuk mendapatkan suara yang lebih jernih, caixa bra…

Role of Muhammad in the Islamic religion This article is about the role and significance of Muhammad in the religion of Islam. For a general overview, see Muhammad. Imam al-Anbiya'Rasul AllahMuhammadمُحَمَّدMuhammad, the Messenger of Godinscribed on the gates of the Prophet's Mosque in MedinaProphet of IslamPreceded byIsa (Jesus)Succeeded byNone TitleKhatam al-Nabiyyin ('Seal of the Prophets')PersonalBornMonday, 12 Rabi' al-Awwal 53 BH (c. 21 April 570 CE) or Saturday, 17 Rabi' al-Awwal …

Disambiguazione – Se stai cercando il torneo disputato tra il 1909 e il 1915 tra i club calcistici dell'Italia meridionale, vedi Coppa Lipton. Copa LiptonSport Calcio TipoNazionali CadenzaAnnuale Partecipanti2 Formulagara unica StoriaFondazione1905 Soppressione1992 Ultimo vincitore Argentina Record vittorie Argentina (17) Trofeo o riconoscimento Modifica dati su Wikidata · Manuale La Copa Lipton (nota anche come Copa de Caridad Lipton) è stato un torneo calcistico disputato tra il 1905 …

For other uses, see Redshirt (disambiguation). Southern US paramilitary organization (post-Civil War) Red ShirtsRed Shirts at a polling place in Old Hundred, North Carolina, on Election Day, November 8, 1898LeadersBenjamin TillmanEllison D. SmithJosephus DanielsClaude KitchinDates of operation1875–1900sAllegianceDemocratic Party (Redeemers)MotivesWhite supremacyHeadquartersSouth CarolinaActive regionsSouthern U.S. (especially The Carolinas)IdeologyWhite supremacyAnti-ReconstructionAlliesR…

Dag Hammarskjöld 2° Segretario generale delle Nazioni UniteDurata mandato10 aprile 1953 –18 settembre 1961 PredecessoreTrygve Lie SuccessoreU Thant Dati generaliPartito politicoindipendente UniversitàUniversità di UppsalaUniversità di Stoccolma Firma Premio Nobel per la pace 1961Dag Hjalmar Agne Carl Hammarskjöld (IPA /dɑːg ˈhammarɧœld/, ascoltaⓘ; Jönköping, 29 luglio 1905 – Ndola, 18 settembre 1961) è stato un diplomatico, economista, scrittore e pubbl…

SejarahVietnam 2879–258 SM Dinasti Hồng Bàng 2879–1913 SM • Hồng Bàng Awal 1912–1055 SM • Hồng Bàng Pertengahan 1054–258 SM • Hồng Bàng Akhir 257–179 SM Dinasti Thục 207–111 SM Dinasti Triệu 111 SM–40 M Dominasi Tiongkok ke-1 40–43 Trưng Bersaudari 43–544 Dominasi Tiongkok ke-2 544–602 Dinasti Lý awal 602–938 Dominasi Tiongkok ke-3 939–967 Dinasti Ngô 968–980 Dinasti Đinh 980–1009 Dinasti Lê Awal 1009–1225 Dinasti Lý akhir 1225–1400 Din…

First DatabankCompany typeSubsidiaryIndustryHealthcareInformation technologyFounded1978; 46 years ago (1978)Headquarters701 Gateway Blvd., Suite 600South San Francisco, California, U.S.Key peopleRobert Katter (presidentCharles Tuchinda executive chairman)Cynthia MacAskill (vice president, finance)Joan Kapusnik-Uner (vice president, Clinical Content)Number of employees400ParentHearst CommunicationsWebsitefdbhealth.com First Databank (FDB) is a major provider of drug and medical …

San AndrésAtas ke bawah, kiri ke kanan: Rumah khas San Andrés, San Andrés Skyline, Johnny Cay, Pantai Spratt Bight, Gereja Baptis Pertama, dan Hotel Matahari TerbitSan AndrésTampilkan peta ColombiaSan AndrésTampilkan peta KaribiaGeografiKoordinat12°35′N 81°42′W / 12.583°N 81.700°W / 12.583; -81.700Koordinat: 12°35′N 81°42′W / 12.583°N 81.700°W / 12.583; -81.700Pulau besarSan Andrés, Providence dan Saint CatherineLuas26 km…

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 外…

圣安东尼奥-杜蒙蒂Santo Antônio do Monte市镇圣安东尼奥-杜蒙蒂在巴西的位置坐标:20°05′13″S 45°17′38″W / 20.0869°S 45.2939°W / -20.0869; -45.2939国家巴西州米纳斯吉拉斯州面积 • 总计1,129.365 平方公里(436.050 平方英里)海拔950 公尺(3,120 英尺)人口 • 總計25,694人 • 密度22.8人/平方公里(58.9人/平方英里) 圣安东尼奥-杜蒙蒂…

Indian film actor and producer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Krishan Kumar actor – news · newspapers · books · scholar · JSTOR (December 2018) (Learn how and when to remove t…

PerssNama lengkapPersatuan Sepakbola SoEJulukanLaskar Wangi Cendana[1]StadionStadion KobeleteKota Soe, Timor Tengah Selatan(Kapasitas: 1,000)PemilikAskab PSSI Timor Tengah SelatanManajerEduard Markus Lioe[2]PelatihApris Misa[3]LigaLiga 32022Babak 16 besar, (Zona NTT) Kostum kandang Kostum tandang Perss (singkatan dari Persatuan Sepakbola SoE) adalah klub sepak bola Indonesia yang bermarkas di Kota Soe, Timor Tengah Selatan, Nusa Tenggara Timur. Tim ini berkompetisi di Lig…