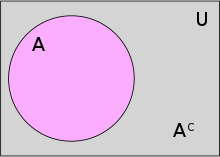
Diagram Venna :
A
c
{\displaystyle A^{c}}
A
{\displaystyle A}
U
.
{\displaystyle U.}
Dopełnienie zbioru , uzupełnienie zbioru [1] [2] [3] [4] zbiór wszystkich elementów (pewnego ustalonego nadzbioru ), które do danego zbioru nie należą[5]
Niech dany będzie zbiór
U
,
{\displaystyle U,}
przestrzenią [1] [2] [4] [6] zbiorem uniwersalnym [4] uniwersum [4]
A
⊆
U
.
{\displaystyle A\subseteq U.}
Dopełnieniem zbioru
A
{\displaystyle A}
różnicę
U
∖
A
=
{
x
∈
U
:
x
∉
A
}
,
{\displaystyle U\setminus A=\{x\in U\colon x\notin A\},}
oznaczaną zwykle symbolem
A
′
{\displaystyle A'}
[1] [2] [3] [6]
A
c
{\displaystyle A^{\operatorname {c} }}
[2] [4]
∁
U
A
{\displaystyle \complement _{U}A}
U
{\displaystyle U}
∁
A
{\displaystyle \complement A}
complement , dopełniać).
Niekiedy spotyka się również oznaczenie
−
A
{\displaystyle -A}
[6]
A
{\displaystyle A}
strukturę algebraiczną , to
−
A
{\displaystyle -A}
{
−
a
:
a
∈
A
}
.
{\displaystyle \{-a\colon a\in A\}.}
Z definicji wynika, że dopełnienie zbioru zależy od wyboru przestrzeni.
Korzystając z pojęcia dopełnienia zbiorów, różnicę zbiorów
A
,
B
⊆
U
{\displaystyle A,B\subseteq U}
A
∖
B
=
A
∩
B
′
.
{\displaystyle A\setminus B=A\cap B'.}
Dla dowolnego uniwersum
U
{\displaystyle U}
∅
′
=
U
,
U
′
=
∅
.
{\displaystyle \varnothing '=U,\quad U'=\varnothing .}
Dla ustalonego
U
{\displaystyle U}
A
⊆
U
{\displaystyle A\subseteq U}
(
A
′
)
′
=
A
,
{\displaystyle (A')'=A,}
co oznacza, że operacja dopełnienia jest inwolucją .
Prawdą jest też, iż zbiór i jego dopełnienie są rozłączne ,
A
∩
A
′
=
∅
,
{\displaystyle A\cap A'=\varnothing ,}
a ich suma daje całe uniwersum,
A
∪
A
′
=
U
,
{\displaystyle A\cup A'=U,}
co oznacza, że
{
A
,
A
′
}
{\displaystyle \{A,A'\}}
rozbiciem zbioru
U
.
{\displaystyle U.}
Dla danych
A
,
B
⊆
U
{\displaystyle A,B\subseteq U}
prawa de Morgana [7]
(
A
∪
B
)
′
=
A
′
∩
B
′
,
{\displaystyle (A\cup B)'=A'\cap B',}
(
A
∩
B
)
′
=
A
′
∪
B
′
.
{\displaystyle (A\cap B)'=A'\cup B'.}
Dodatkowo
B
=
A
′
{\displaystyle B=A'}
B
′
=
A
.
{\displaystyle B'=A.}
Dopełnieniem zbioru
{
1
,
2
}
{\displaystyle \{1,2\}}
{
1
,
2
,
3
}
{\displaystyle \{1,2,3\}}
{
3
}
.
{\displaystyle \{3\}.}
Dopełnieniem zbioru liczb wymiernych w zbiorze liczb rzeczywistych jest zbiór liczb niewymiernych .
Dopełnieniem prostej na płaszczyźnie euklidesowej jest suma dwóch rozłącznych otwartych półpłaszczyzn .
Dopełnieniem zbioru
{
0
,
1
,
2
}
{\displaystyle \{0,1,2\}}
liczb naturalnych jest zbiór liczb naturalnych większych od
2
,
{\displaystyle 2,}
{
−
1
,
0
,
1
,
2
,
3
,
4
,
5
}
{\displaystyle \{-1,0,1,2,3,4,5\}}
{
−
1
,
3
,
4
,
5
}
.
{\displaystyle \{-1,3,4,5\}.}
Przypisy
↑ a b c Rozdział I (pdf) . W: Kazimierz Kuratowski , Andrzej Mostowski : Teoria mnogości ↑ a b c d Kazimierz Kuratowski , Ryszard Engelking : Wstęp do teorii mnogości i topologii . Warszawa: Wydawnictwo Naukowe PWN, 2004, s. 16,17. ISBN 83-01-14215-4 .↑ a b Wojciech Guzicki, Piotr Zakrzewski: Wykłady ze wstępu do matematyki: wprowadzenie do teorii mnogości . Warszawa: Wydawnictwo Naukowe PWN, 2005, s. 15. ISBN 83-01-14415-7 . ↑ a b c d e Kenneth A. Ross, Charles R.B Wright: Matematyka dyskretna . E. Sepko-Guzicka (tłum.), W. Guzicki (tłum.), P. Zakrzewski (tłum.). Warszawa: Wydawnictwo Naukowe PWN , 1996, s. 27–31. ISBN 83-01-12129-7 . ↑ dopełnienie zbioru Encyklopedia PWN Wydawnictwo Naukowe PWN [dostęp 2023-09-06] .↑ a b c Wiktor Marek, Janusz Onyszkiewicz : Elementy logiki i teorii mnogości w zadaniach . Warszawa: Państwowe wydawnictwo naukowe, 1975, s. 19. ↑ Angielski logik Augustus De Morgan odkrył przedstawione prawa rachunku zbiorów. Analogiczne prawa rachunku zdań sformułowano później, ale zwykło się je nazywać również nazwiskiem de Morgana Rozdział IV. Algebra zbiorów i relacji (pdf) . W: Andrzej Mostowski : Logika matematyczna