Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW  • CAPES  • Google (notícias • livros • acadêmico)). (Março de 2014)

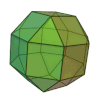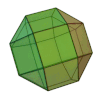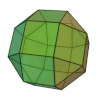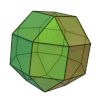
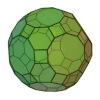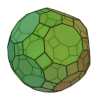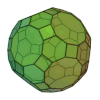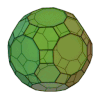
Os sólidos de Arquimedes ou poliedros semi-regulares são poliedros convexos cujas faces são polígonos regulares de mais de um tipo. Todos os seus vértices são congruentes, isto é, existe o mesmo arranjo de polígonos em torno de cada vértice.^[1] Além disso, todo vértice pode ser transformado em outro vértice por uma simetria do poliedro. Existem apenas treze poliedros arquimedianos e são todos obtidos por operações sobre os sólidos platónicos.

Onze são obtidos truncando sólidos platónicos:

O tetraedro truncado, o cuboctaedro, o cubo truncado, o octaedro truncado, o rombicuboctaedro, o cuboctaedro truncado, o icosidodecaedro, o dodecaedro truncado, o icosaedro truncado, o rombicosidodecaedro e o icosidodecaedro truncado.

Dois que são obtidos por snubificação de sólidos platónicos:

O cubo snub e o icosidodecaedro snub. Estes dois sólidos têm caso isomórfico, quer dizer uma figura de espelho correspondente.

Sólidos de Arquimedes
Tetraedro truncado Dual: tetraedro triakis		8 faces 4 triángulos 4 hexágonos	12 vértices	18 arestas
Cuboctaedro Dual: dodecaedro rómbico		14 faces 8 triângulos 6 quadrados	12 vértices	24 arestas
Cubo truncado Dual: octaedro triakis		14 faces 8 triângulos 6 octogonos	24 vértices	36 arestas
Octaedro truncado Dual: hexaedro tetrakis		14 faces 6 quadrados 8 hexágonos	24 vértices	36 arestas
Rombicuboctaedro ou pequeno rombicuboctaedro Dual: icositetraedro deltoidal		26 faces 8 triângulos 18 quadrados	24 vértices	48 arestas
Cuboctaedro truncado ou grande rombicuboctaedro Dual: dodecaedro disdiakis		26 faces 12 quadrados 8 hexágonos 6 octógonos	48 vértices	72 arestas
Icosidodecaedro Dual: triacontaedro rómbico		32 faces 20 triângulos 12 pentágonos	30 vértices	60 arestas
Dodecaedro truncado Dual: icosaedro triakis		32 faces 20 triângulos 12 decágonos	60 vértices	90 arestas
Icosaedro truncado ou bola de futebol Dual: dodecaedro pentakis		32 faces 12 pentágonos 20 hexágonos	60 vértices	90 arestas
Rombicosidodecaedro ou pequeno rombicosidodecaedro Dual: hexecontaedro deltoidal		62 faces 20 triângulos 30 quadrados 12 pentágonos	60 vértices	120 arestas
Icosidodecaedro truncado ou grande rombicosidodecaedro Dual: triacontaedro disdiakis		62 faces 30 quadrados 20 hexágonos 12 decágonos	120 vértices	180 arestas
Cubo snub ou Cuboctaedro Snub Este poliedro tem um caso isomórfico Dual: Icositetraedro pentagonal		38 faces 32 triângulos 6 quadrados	24 vértices	60 arestas
Icosidodecaedro snub ou dodecaedro snub Este poliedro tem um caso isomórfico Dual: hexecontaedro pentagonal		92 faces 80 triângulos 12 pentágonos	60 vértices	150 arestas

Os sólidos de Arquimedes, têm o nome de Arquimedes, que os descobriu e relatou em livros que se perderam.

Durante a Renascença, artistas e matemáticos descobriram de novo todos os sólidos de Arquimedes. As descobertas ficaram completas à volta de 1619, por Johannes Kepler, que definiu prismas, antiprismas e poliedros não convexos conhecidos como poliedros de Kepler-Poinsot.

Os duais dos sólidos de Arquimedes são chamados sólidos de Catalan.

Foram descritos pela primeira vez pelo matemático belga Eugène Catalan em 1865.

Os sólidos de Catalan são 13: o tetraedro triakis; o dodecaedro rômbico; o octaedro triakis; o hexaedro tetrakis; o icositetraedro deltoidal; o dodecaedro disdiakis; o icositetraedro pentagonal; o triacontaedro rômbico; o icosaedro triakis; o dodecaedro pentakis; o hexecontaedro deltoidal; o triacontaedro disdiakis e o hexecontaedro pentagonal.

Referências