泛性质

在数学的很多分支，经常用“在给定某些条件下存在唯一态射”这种形式的性质来定义一些构造。这种性质统称为泛性质（英語：Universal property），有时也称为万有性。范畴论研究泛性质。

了解泛性质最好先研究一些例子。如：群积、直和、自由群、积拓扑、斯通-切赫紧致、张量积、反极限、直极限、核与上核、拉回、推出、等子等。

设U : D → C为一函子，X为C的对象。从X到U的泛态射为偶(A, φ)，其中A为D的对象，φ : X → U(A)为C中满足如下泛性质的态射：

• 对任意D的对象Y和任意C的态射f : X → U(Y)，存在唯一的态射g : A → Y使得下图可交换：

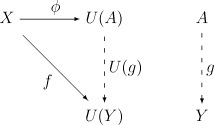态射g的存在保证A具有足够的性质，其唯一性又限制A不再有额外的性质。

使用对偶原则可得上述的对偶概念：从U到X的泛态射为偶(A, φ)，其中A为D的对象，φ : U(A) → X为C的态射，满足如下泛性质：

• 对任意D的对象Y和任意C的态射f : U(Y) → X，存在唯一的态射g : Y → A使得下图可交换：

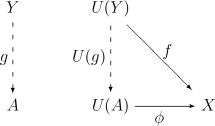注：有时后者也称为上泛态射。

具有泛性质的构造不一定存在。给定上述函子U和对象X，从X到U（或从U到X）的泛态射不一定存在。然而，若其存在，则该构造在同构下唯一。也就是说，若(A′, φ′)为另一个满足该条件的泛态射，则存在唯一的同构态射g : A → A′满足φ′ = U(g)φ。用(A′, φ′)代替定义中的(Y, f)易知该结论成立。

泛态射可通过其它途径定义。设U为从D到C的函子，X为C的对象，则下列语句等价：

• (A, φ)为从X到U的泛态射
• (A, φ)为逗号范畴(X ↓ U)的始对象
• (A, φ)为Hom_C(X, U—)的表示。

其对偶语句也同样等价：

• (A, φ)为从U到X的泛态射
• (A, φ)为逗号范畴(U ↓ X)的终对象
• (A, φ)为Hom_C(U—, X)的表示。

设(A₁, φ₁)为从X₁到U的泛态射，(A₂, φ₂)为从X₂到U的泛态射。根据泛性质，对任意态射h : X₁ → X₂，存在唯一态射g : A₁ → A₂使得下图可交换：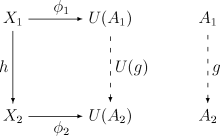

若对任意C的对象X_i存在到U的泛态射，则映射X_i ${\displaystyle \mapsto }$ A_i和h ${\displaystyle \mapsto }$ g确定一个函子 V : C → D。此时，φ_i确定从1_C（C上的恒等函子）到U V的一个自然变换。因此(V, U)构成一对伴随函子，V左伴随U，U右伴随V。

利用对偶原则同样可得U的右伴随函子V : C → D。

事实上，所有的伴随函子都产生与类似的泛构造。设F和G为一对伴随函子，单位元为&eta，上单位元为&epsilon（定义见伴随函子）。任意C和D的对象存在泛态射。

• 对任意C的对象X，(F(X), η_X)为从X到G的泛态射。即，对任意f : X → G(Y)，存在唯一g : F(X) → Y使得下图可交换。
• 对任意D的对象Y，(G(Y), ε_Y)为从F到Y的泛态射。即，对任意g : F(X) → Y，存在唯一f : X → G(Y)使得下图可交换。

泛构造的概念广于伴随函子：泛构造类似优化问题，伴随函子存在当且仅当该优化问题对任何C的对象（或对任何D的对象）均存在解。

设C为域K上的向量空间范畴 K-Vect，D为K上的代数范畴（假定满足unitall和结合律），U为将代数映射为所基向量空间的遗忘函子。

给定任何基于K的向量空间V，构造V的张量代数T(V)。此张量代数的泛性质体现为偶(T(V), i)（其中i : V → T(V)为一inclusion map）是从V到U的泛态射。

由于此方法适用于任何V，因此T为从K-Vect到K-Alg的函子，且为U的左伴随。

设D为一存在零态射的范畴（如群范畴），f : X → Y为D的一态射。f的核为满足下列条件的任意态射k : K → X：

• f k为从K到Y的零态射；
• 对任意态射k′ : K′ → X，若f k′为零态射，则存在唯一态射u : K′ → K满足k u = k′。

为理解上述同泛态射的关系，定义D中态射的范畴C，对象为D的所有态射f : X → Y，从f : X → Y到g : S → T的态射为一对态射α : X → S和β : Y → T构成的偶(α, β)，满足βf = fα。

定义函子F : D → C，映射对象K到零态射0_KK : K → K，映射态射r : K → L到偶(r, r)。

给定D的态射f : X → Y（看作C的对象）及D的对象K。从F(K)到f的态射为偶(k, l)满足f k = l 0_KK = 0_KY（此即为上述核的泛性质）。可以看出，“从F到f的泛态射”即为核的泛性质。

极限与上极限为范畴论中重要的泛构造。设J为小范畴、C为范畴，J看作为C的索引范畴。记C^J为相应的函子范畴。对角函子 Δ : C → C^J 将C中每个对象N映射到常函子Δ(N) : J → C to N (i.e. 对任意X属于J有Δ(N)(X) = N).

给定函子F : J → C（看作C^J的对象），F的极限，若存在，即为从Δ到F的泛态射。由对偶性质，F的上极限为F到Δ的泛态射。

使用泛性质定义构造有如下优点：

• 泛性质定义的对象在同构下唯一，因此证明两个对象同构的一个方法是找出其同时满足的泛性质。
• 定义某构造的具体细节一般较为繁琐，利用泛性质可不考虑这些细节，证明往往变得简洁明了。
• 如果泛构造对任何对象都存在时可确定一个函子。
• 更进一步，该函子为U的伴随函子。此时可以利用右伴随和极限可交换（左伴随和上极限可交换）的性质。

Pierre Samuel在1948年给出了多种拓扑结构的泛性质。布尔巴基大量使用了其结论。丹尼尔·阚与1958年独立发现了与其密切相关的伴随函子概念。

• Cohen, Paul M., Universal Algebra (1981), D.Reidel Publishing, Holland. ISBN 90-277-1213-1.
• Mac Lane, Saunders, Categories for the Working Mathematician 2nd ed. (1998), Graduate Texts in Mathematics 5. Springer. ISBN 0-387-98403-8.