系列条目
量子力学
${\displaystyle i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle ={\hat {H}}|\psi (t)\rangle }$ 薛定谔方程
入门 术语（英语：Glossary of elementary quantum mechanics） 历史
背景 经典力学 舊量子論 狄拉克符号 哈密顿算符 干涉
基本原理 互补 退相干 纠缠 能级 测量 非局域性（英语：Quantum nonlocality） 量子数 量子態 态叠加原理 对称性（英语：Symmetry in quantum mechanics） 量子穿隧效應 不确定性 波函数 波函数坍缩
实验 貝爾定理的實驗驗證 戴維森-革末實驗 雙縫實驗 伊利澤-威德曼炸彈測試問題 法蘭克-赫茲實驗 Leggett-Garg不平等现象（英语：Leggett–Garg inequality） 馬赫-曾德爾干涉儀 波普尔实验 量子擦除實驗 延遲選擇 薛定谔猫 施特恩-格拉赫实验 惠勒延迟选择实验
表述 概览 海森堡繪景 相互作用繪景 矩陣力學 相空间表述 薛丁格繪景 路徑積分表述
方程 狄拉克方程式 克莱因-戈尔登方程 包立方程式 里德伯公式 薛定谔方程
诠释 概览 量子贝叶斯主义（英语：Quantum Bayesianism） 一致性历史 哥本哈根詮釋 德布罗意-玻姆理论 系綜詮釋 隱變量理論 局部隐变量（英语：Local hidden-variable theory） 多世界诠释 客觀坍縮理論 量子逻辑（英语：Quantum logic） 關係性量子力學 交易詮釋
高阶 相对论量子力学 量子场论 量子信息科学 量子计算 量子混沌（英语：Quantum chaos） 密度矩陣 散射理论（英语：Scattering theory） 量子统计力学 量子機器學習
科学家 阿哈罗诺夫 貝爾 贝特 布莱克特 布洛赫 玻姆 玻尔 玻恩 玻色 德布罗意 康普顿 狄拉克 戴维孙 德拜 埃伦费斯特 爱因斯坦 艾弗雷特三世 福克 费米 費曼 格劳伯 古茨威勒 海森堡 希尔伯特 约尔旦 克喇末 泡利 兰姆 朗道 劳厄 莫塞莱 密立根 昂內斯 普朗克 拉比 拉曼 里德伯 薛定谔 米歇尔·西蒙斯（英语：Michelle Simmons） 索末菲 冯·诺伊曼 外尔 维恩 维格纳 塞曼 蔡林格
查 论 编

在量子力學以及其應用如多體問題、量子化學等領域中，角動量圖是一種圖形表示法，用以代表一量子系統的角動量量子態，使得相關計算能以符號形式推演。此方法的箭號將角動量態與狄拉克符號連結。

此方法是由立陶宛物理學家阿朵發斯‧朱西斯（英语：Adolfas Jucys）於20世紀發明。在量子力學以及量子場論領域中，形似的符號表示法尚有費曼圖與潘洛斯圖形符號。這些圖樣包含有箭頭與頂點，有些還有量子數的標記。

單一粒子帶有總角動量量子數j與總磁量子數m = j, j − 1, ..., −j + 1, −j，其量子態向量以狄拉克符號的右矢（Ket）標記為|j, m⟩，其圖形則為單箭頭的箭號。有一相對應的左矢（Bra）為⟨j, m|，其圖形為雙箭頭的箭號，指向與右矢相反。

例子中

• 量子數j、m常標記在箭頭附近，以表示特定的角動量量子態，
• 箭頭常在線段的中間
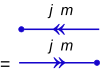
• 等號"="置於等價的圖樣之間，如同相應的代數運算。

最基本的左矢與右矢圖形符號為：

右矢 |j, m⟩

左矢 ⟨j, m|

箭號指向頂點或從頂點指出，分別為

• 標準表象（standard representation）以一條離開頂點的指向線段表示，
• 反標準表象（contrastandard representation）則是以一條進入頂點的指向線段表示。

箭號一個一個相接續。在反標準表象中，採用時間反轉算符T。T算符是么正的，也就是其厄米伴算符T^†等於其反算符T⁻¹，即T^† = T⁻¹。其作用在位置算符時，結果保持不變：

${\displaystyle T{\hat {\mathbf {x} }}T^{\dagger }={\hat {\mathbf {x} }}}$

線動量算符則變為負值：

${\displaystyle T{\hat {\mathbf {p} }}T^{\dagger }=-{\hat {\mathbf {p} }}}$

自旋算符也變為負值：

${\displaystyle T{\hat {\mathbf {S} }}T^{\dagger }=-{\hat {\mathbf {S} }}}$

既然軌域角動量算符L = x × p，在T算符作用後也會變為負值：

${\displaystyle T{\hat {\mathbf {L} }}T^{\dagger }=-{\hat {\mathbf {L} }}}$

也因此總角動量算符J = L + S也變為負值：

${\displaystyle T{\hat {\mathbf {J} }}T^{\dagger }=-{\hat {\mathbf {J} }}}$

作用在角動量算符本徵態|j, m⟩，可得：（見註釋）

${\displaystyle T\left|j,m\right\rangle \equiv \left|T(j,m)\right\rangle ={(-1)}^{j-m}\left|j,-m\right\rangle }$

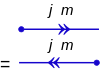
時間反轉的圖形符號為：

時間反轉右矢|j, m⟩.

時間反轉左矢⟨j, m|.

將頂點標記在正確位置相當重要，否則正向時間與反向時間的算符會相互混淆。

狀態|j₁, m₁⟩與狀態|j₂, m₂⟩的內積：

${\displaystyle \langle j_{2},m_{2}|j_{1},m_{1}\rangle =\delta _{j_{1}j_{2}}\delta _{m_{1}m_{2}}}$

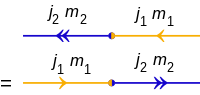
相應的圖形符號為：

|j₁, m₁⟩與|j₂, m₂⟩的內積，亦即⟨j₂, m₂|j₁, m₁⟩

時間反轉等價

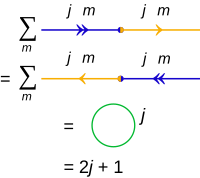
將內積加總，也就是縮併的計算：

${\displaystyle \sum _{m}\langle j,m|j,m\rangle =2j+1}$

習慣上會以一封閉圓來表示，並且標上j：

狀態|j₁, m₁⟩與狀態|j₂, m₂⟩的外積是一算符：

${\displaystyle \left|j_{2},m_{2}\right\rangle \left\langle j_{1},m_{1}\right|}$

相對應的圖形符號為：

|j₁, m₁⟩與|j₂, m₂⟩的外積，亦即|j₂, m₂⟩⟨j₁, m₁|

時間反轉等價

將外積加總，也就是縮併的計算：

${\displaystyle {\begin{aligned}\sum _{m}|j,m\rangle \langle j,m|&=\sum _{m}|j,-m\rangle \langle j,-m|\\&=\sum _{m}{(-1)}^{2(j-m)}|j,-m\rangle \langle j,-m|\\&=\sum _{m}{(-1)}^{j-m}|j,-m\rangle \langle j,-m|{(-1)}^{j-m}\\&=\sum _{m}T|j,m\rangle \langle j,m|T^{\dagger }\end{aligned}}}$

時間反轉算符T的結果可見於上式T|j, m⟩。對外積縮併計算來縮，正向時間與反向時間沒有差別，因此圖形符號表示是相同的，皆為一無指向的線段，其上僅標示j：

n狀態|j₁, m₁⟩, |j₂, m₂⟩, ... |j_n, m_n⟩的張量積⊗可寫為：

${\displaystyle {\begin{aligned}\left|j_{1},m_{1},j_{2},m_{2},...j_{n},m_{n}\right\rangle &\equiv \left|j_{1},m_{1}\right\rangle \otimes \left|j_{2},m_{2}\right\rangle \otimes \cdots \otimes \left|j_{n},m_{n}\right\rangle \\&\equiv \left|j_{1},m_{1}\right\rangle \left|j_{2},m_{2}\right\rangle \cdots \left|j_{n},m_{n}\right\rangle \end{aligned}}}$

圖形符號則呈扇形——n項個別態的線段匯聚於一共同頂點。

頂點附近標有一正負號，以表示張量積的順序：

• 負號(−)表示順序為順時針走向${\displaystyle \circlearrowright }$，
• 正號(+)表示順序為逆時針走向${\displaystyle \circlearrowleft }$.

有時候會在正負號之外，加上彎箭頭來表示上述的走向。

|j₁, m₁⟩, |j₂, m₂⟩, |j₃, m₃⟩的張量積，亦即|j₁, m₁⟩|j₂, m₂⟩|j₃, m₃⟩ = |j₁, m₁, j₂, m₂, j₃, m₃⟩

時間反轉等價

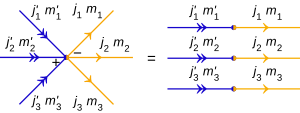
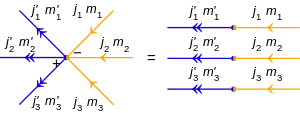
兩張量積態的內積：

${\displaystyle {\begin{aligned}&\left\langle j'_{n},m'_{n},...,j'_{2},m'_{2},j'_{1},m'_{1}|j_{1},m_{1},j_{2},m_{2},...j_{n},m_{n}\right\rangle \\=&\langle j'_{n},m'_{n}|...\langle j'_{2},m'_{2}|\langle j'_{1},m'_{1}||j_{1},m_{1}\rangle |j_{2},m_{2}\rangle ...|j_{n},m_{n}\rangle \\=&\prod _{k=1}^{n}\left\langle j'_{k},m'_{k}|j_{k},m_{k}\right\rangle \end{aligned}}}$

|j′₁, m′₁, j′₂, m′₂, j′₃, m′₃⟩與|j₁, m₁, j₂, m₂, j₃, m₃⟩的內積，亦即⟨j′₃, m′₃, j′₂, m′₂, j′₁, m′₁|j₁, m₁, j₂, m₂, j₃, m₃⟩

時間反轉等價

• 角動量
• 狄拉克符號
• 克萊布希－高登係數
• 角動量算符
• 階梯算符
• 費曼圖

• P.E.S. Wormer, J. Paldus. Angular Momentum Diagrams 51. Elsevier. 2006: 59–124 [2015-03-18]. ISSN 0065-3276. doi:10.1016/S0065-3276(06)51002-0. （原始内容存档于2019-04-11）.  |journal=被忽略 (帮助) These authors use the theta variant ϑ for the time reversal operator, here we use T.

• I. Lindgren, J. Morrison. Atomic Many-Body Theory. Chemical Physics 13 2nd. Springer-Verlag. 1986 [2015-03-18]. ISBN 3-540-166-491. （原始内容存档于2015-04-02）. 

• G.W.F. Drake. Springer Handbook of Atomic, Molecular, and Optical Physics 2nd. springer. 2006: 60 [2015-03-18]. ISBN 0-3872-6308-X. （原始内容存档于2015-04-09）. 

• U. Kaldor, S. Wilson. Theoretical Chemistry and Physics of Heavy and Superheavy Elements. Progress in Theoretical Chemistry and Physics 11. springer. 2003: 183 [2015-03-18]. ISBN 1-4020-1371-X. （原始内容存档于2015-04-11）. 

• E.J. Brändas, P.O. Löwdin, E. Brändas, E.S. Kryachko. Fundamental World of Quantum Chemistry: A Tribute to the Memory of Per-Olov Löwdin 3. Springer. 2004: 385 [2015-03-18]. ISBN 1-402-025-831. （原始内容存档于2015-04-07）. 

• P. Schwerdtfeger. Relativistic Electronic Structure Theory: Part 2. Applications. Theoretical and Computational Chemistry 14. Elsevier. 2004: 97 [2015-03-18]. ISBN 008-054-047-3. （原始内容存档于2015-04-07）. 

• M. Barysz, Y. Ishikawa. Relativistic Methods for Chemists. Challenges and advances in computational chemistry and physics 10. Springer. 2010: 311 [2015-03-18]. ISBN 1-402-099-754. （原始内容存档于2015-04-06）. 

• G.H.F. Diercksen, S. Wilson. Methods in Computational Molecular Physics. Nato Science Series C 113. Springer. 1983 [2015-03-18]. ISBN 9-027-716-382. （原始内容存档于2015-04-10）. 

• Zenonas Rudzikas. 8. Theoretical Atomic Spectroscopy. Cambridge Monographs on Atomic, Molecular and Chemical Physics 7. University of Chicago: Cambridge University Press. 2007 [2015-03-18]. ISBN 0-521-026-229. （原始内容存档于2015-04-05）. 

• Lietuvos Fizikų draugija. Lietuvos fizikos žurnalas 44. University of Chicago: Draugija. 2004 [2015-03-18]. （原始内容存档于2014-08-19）. 

• P.E.T. Jorgensen. Operators and Representation Theory: Canonical Models for Algebras of Operators Arising in Quantum Mechanics. University of Chicago: Elsevier. 1987 [2015-03-18]. ISBN 008-087-258-1. （原始内容存档于2015-04-10）.