ترقيم السنة الفلكية
|
Read other articles:

GambitCover X-Men: Endangered Species Part 1-Blinded by the Light Part 1 of 4Karya Chris Bachalo.Informasi publikasiPenerbitMarvel ComicsPenampilan pertamaUncanny X-Men Annual #14dan Uncanny X-Men #266Dibuat olehChris Claremont (penulis)Jim Lee (ilustrasi)Informasi dalam ceritaAlter egoRemy Etienne LeBeauSpesiesManusia MutanAfiliasi timX-FactorX-MenMaraudersHorsemen of ApocalypseXSELeBeau ClanThieves' GuildCrimson PiratesJean Grey SchoolNama alias terkenalLe Diable Blanc, Robert Lord, Death, Rag…

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Pegunungan Muller – berita · surat kabar · buku · cendekiawan · JSTOR Pegunungan Muller Negara Indonesia Titik tertinggi Gunung Liangpran Pegunungan Muller merupakan jajaran pegunungan yang berada di batas …

Kebudayaan India terbagi menjadi lima wilayah geografis utama. Cerita rakyat India merupakan cerita rakyat yang ada di negara India dan subbenua India. Subbenua India terdiri dari pembagian etnis, bahasa, dan agama yang luas. Dengan pembagian ini, sulit untuk menggeneralisasikan mengenai cerita rakyat India sebagai suatu satuan. Artikel bertopik mitologi, mitos, atau legenda ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Busyra ZahirLahirBoesjra Zahir(1921-08-19)19 Agustus 1921Koto Gadang, Agam, Hindia BelandaKebangsaanIndonesiaPekerjaanPengajarDikenal atasRektor Universitas Andalas Prof. Dr. Busyra Zahir (lahir 19 Agustus 1921)[1][2] adalah seorang tokoh pengajar dan ahli kesehatan Indonesia. Ia merupakan rektor yang ke-4 pada Universitas Andalas (Unand), Padang, Sumatera Barat. Busyra menggantikan rektor sebelumnya, Prof. Drs. Harun Alrasjid Zain, pada tahun 1968. Ia menjabat rektor selama dua …
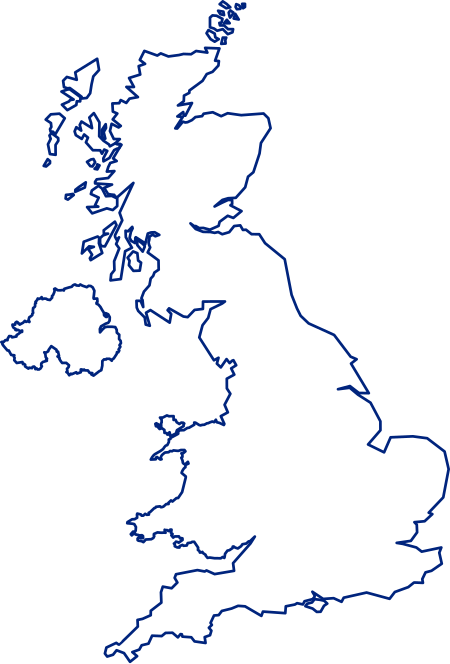
Wilayah Pegunungan Pennine di utara Inggris Pennines adalah barisan pegunungan dengan ketinggian rendah di utara Inggris dan Skotlandia selatan. Pegunungan ini memisahkan Inggris Barat Laut dari Yorkshire dan Inggris Timur Laut. Sering dikatakan sebagai 'tulang punggung Inggris',[1][2][3] mereka membentuk rangkaian yang membentang dari Peak District di Derbyshire, melalui Yorkshire Dales, di pinggiran utara dan timur Manchester Raya, West Pennine Moors dari Lancashire dan…

Bendera Brunei Darussalam Pemakaian Bendera sipil dan negara; bendera kapal sipil Perbandingan 1:2 Dipakai 29 September 1959 Rancangan Bidang kuning yang dibelah dua garis yang berwarna putih dan hitam secara diagonal; serta lambang Brunei di tengahnya. Perancang Yura Halim Bendera Brunei diperkenalkan pada 29 September 1959 semasa Brunei merupakan protektorat Britania Raya dan ditetapkan saat Brunei mencapai kemerdekaan pada 1 Januari 1984. Bendera ini terdiri dari lambang negara di bagian teng…

WAY-629 Names IUPAC name 1,2,3,4,8,9,10,11-Octahydro[1,4]diazepino[6,7,1-jk]carbazole Identifiers CAS Number 57756-44-2 Y 3D model (JSmol) Interactive image ChEBI CHEBI:92969 ChEMBL ChEMBL258465 ChemSpider 5037189 PubChem CID 6604933 UNII S3TQZ8FAS2 Y CompTox Dashboard (EPA) DTXSID0043890 InChI InChI=1S/C15H18N2/c1-2-7-14-12(5-1)13-6-3-4-11-10-16-8-9-17(14)15(11)13/h3-4,6,16H,1-2,5,7-10H2Key: OIGHTPDWPMLMGT-UHFFFAOYSA-NInChI=1/C15H18N2/c1-2-7-14-12(5-1)13-6-3-4-11-10-16-8-9-17(14)…

« Pays du Nord » redirige ici. Pour la revue locale du nord de la France, voir Pays du Nord (magazine). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (août 2016). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant …

Dinu Adameșteanu in un ritratto giovanile (Roma, 1940) Dinu Adameșteanu (Toporu, 25 marzo 1913 – Policoro, 21 gennaio 2004) è stato un archeologo rumeno naturalizzato italiano, pioniere e promotore dell'applicazione delle tecniche di aerofotografia e prospezione aerea nella ricerca e ricognizione archeologica. Dal 1958 al 1964, fu direttore della Aerofototeca del Ministero della pubblica istruzione; fu professore, all'Università di Lecce, di Etruscologia e antichità italiche, di topografi…

Murder committed in Polstead, Suffolk, England in 1827 Murder in the Red Barn redirects here. For the 1935 film, see Maria Marten, or The Murder in the Red Barn. Maria Marten redirects here. For other uses, see Maria Marten (disambiguation). The Red Barn, so called for the red clay-tiled roof to the left of its main door. The remaining roof was thatched. The Red Barn Murder was a 1827 murder in Polstead, Suffolk, England. A young woman, Maria Marten, was shot dead by her lover William Corder at …

Tour Down Under 2018 GénéralitésCourse20e Tour Down UnderCompétitionUCI World Tour 2018 2.UWTÉtapes6Dates16 – 21 janvier 2018Distance783,8 kmPays AustralieLieu de départPort AdelaideLieu d'arrivéeAdélaïdeÉquipes19Partants131Arrivants125Vitesse moyenne39,073 km/hSite officielSite officielRésultatsVainqueur Daryl Impey (Mitchelton-Scott)Deuxième Richie Porte (BMC Racing Team)Troisième Tom-Jelte Slagter (Dimension Data)Classement par points Peter Sagan (Bora-Hansgrohe)Meilleur grimpe…

Peta infrastruktur dan tata guna lahan di Komune Rozay-en-Brie. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiRozay-en-BrieNegaraPrancisArondisemenProvinsKantonRozay-en-BrieAntarkomuneCommunauté de communes Les Sources de l'YerresPemerintahan • Wali kota (2008-2014) Patrick Percik • Populasi12.613Kode INSEE/pos77393 / 2 Population sans …

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (novembre 2021). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Marco Minghetti Fonctions Président du Conseil des …

47th quadrennial U.S. presidential election 1972 United States presidential election ← 1968 November 7, 1972 1976 → 538 members of the Electoral College270 electoral votes needed to winTurnout56.2%[1] 6.3 pp Nominee Richard Nixon George McGovern Party Republican Democratic Home state California South Dakota Running mate Spiro Agnew Sargent Shriver(replacing Thomas Eagleton) Electoral vote 520[a] 17 States carried 49 1 + DC Popular&…
1946 animated short film by Bob Clampett The Big SnoozeTitle cardDirected byBob Clampett (uncredited)Story byBob Clampett (uncredited)StarringMel BlancMusic byCarl StallingAnimation byRod ScribnerI. EllisManny GouldJ.C. MelendezLayouts byThomas McKimsonBackgrounds byPhilip DeGuardColor processTechnicolorProductioncompanyWarner Bros. CartoonsDistributed byWarner Bros. PicturesThe Vitaphone CorporationRelease date October 5, 1946 (1946-10-05) Running time7:25CountryUnited StatesLang…

Recipient of the Victoria Cross For other people with the same name, see John Thomas. John ThomasBorn(1886-05-10)10 May 1886Manchester, Lancashire, EnglandDied28 February 1954(1954-02-28) (aged 67)Stockport, Cheshire, EnglandBuriedStockport Borough Cemetery, StockportAllegiance United KingdomService/branch British ArmyRankSergeantUnitNorth Staffordshire RegimentBattles/warsWorld War IAwards Victoria Cross John Thomas VC (10 May 1886 – 28 February 1954) was an English recipie…

Progress M-14MProgress M-14M approaches theISS on 27 January 2012.Mission typeISS resupplyOperatorRoskosmosCOSPAR ID2012-004A SATCAT no.38073Mission duration94 days Spacecraft propertiesSpacecraft typeProgress-M s/n 414ManufacturerRKK Energia Start of missionLaunch date25 January 2012, 23:06:40 UTCRocketSoyuz-ULaunch siteBaikonur, Site 1/5[1] End of missionDisposalDeorbitedDecay date28 April 2012 Orbital parametersReference systemGeocentricRegimeLow EarthPerigee altitude193 kmApogee…

Questa voce sull'argomento contee dell'Illinois è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di OgleconteaLocalizzazioneStato Stati Uniti Stato federato Illinois AmministrazioneCapoluogoOregon Data di istituzione1836 TerritorioCoordinatedel capoluogo42°02′24″N 89°19′12″W / 42.04°N 89.32°W42.04; -89.32 (Contea di Ogle)Coordinate: 42°02′24″N 89°19′12″W / 42.04°N 89.32°W42.04; -89.…

American businessman and politician Craig Greenberg51st Mayor of LouisvilleIncumbentAssumed office January 2, 2023Preceded byGreg Fischer Personal detailsBorn (1973-08-22) August 22, 1973 (age 50)Commack, New York, U.S.Political partyDemocraticSpouseRachelChildren2EducationUniversity of Michigan (BS)Harvard University (JD)WebsiteCampaign website Craig Greenberg (born August 22, 1973) is an American businessman, lawyer, and politician[1] serving as the third mayor of Louisville M…

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「弐」…