History of classical mechanics
|
Read other articles:

Sampul buku Asterix dan Cleopatra. Asterix dan Cleopatra, adalah buku ke-6 dari serial buku komik Asterix buatan René Goscinny dan Albert Uderzo, yang dibuat pada tahun 1965 dan diterjemahkan kedalam bahasa Inggris pada tahun 1969. Buku ini telah diadaptasikan kedalam film, yaitu Asterix and Cleopatra) tahun 1968 dan Asterix & Obelix: Mission Cleopatra tahun 2002. Artikel bertopik buku ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Bassey IkpiBassey Ikpi pada 2016Lahir03 Agustus 1976 (umur 47)Ikom, Cross River State, NigeriaKebangsaanNigeria, Amerika SerikatPekerjaanPenyair, penulis, aktivis kesehatan mental Bassey Ikpi (lahir 3 Agustus 1976) adalah penyair, penulis, dan penasihat kesehatan jiwa.[1] Dia telah tampil di HBO's Russell Simmons Presents Poetry Def lima kali dan puisinya telah membuka pertunjukan untuk artis pemenang Grammy Award. Dia juga penulis terlaris New York Times dari I'm Telling the Truth …

هوينبرغ أن در إيغر شعار الإحداثيات 50°06′00″N 12°13′00″E / 50.1°N 12.216666666667°E / 50.1; 12.216666666667 [1] تقسيم إداري البلد ألمانيا[2] التقسيم الأعلى منطقة فونزيدل خصائص جغرافية المساحة 15.66 كيلومتر مربع (31 ديسمبر 2017)[3] ارتفاع 525 متر عدد ال…

2011 film Miss BalaCinematic release posterDirected byGerardo NaranjoWritten byGerardo NaranjoMauricio KatzProduced byPablo CruzStarringStephanie SigmanCinematographyMátyás ErdélyEdited byGerardo NaranjoMusic byEmilio KaudererProductioncompaniesCanana FilmsFox International Productions[1]Distributed byFox International Productions[1] (through 20th Century Fox)Release dates 13 May 2011 (2011-05-13) (Cannes) 9 September 2011 (2011-09-09) (Me…

Pour les articles homonymes, voir Liste des saints. La première des huit fresques de la Procession des saints de Bretagne ornant le déambulatoire de la Cathédrale Saint-Pierre de Rennes. Page de garde du livre la vie des bienheureux et des saints de Bretagne, pour tous les jours de l'année de Malo-Joseph de Garaby. Les saints bretons désignent des personnalités vénérées pour le caractère exemplaire de leur vie d'un point de vue chrétien et les miracles qu'ils ont accompli. Bien que pe…

Coppa del Brasile 2001Copa do Brasil 2001 Competizione Coppa del Brasile Sport Calcio Edizione 13ª Organizzatore CBF Date dal 14 marzo 2001al 17 giugno 2001 Luogo Brasile Partecipanti 64 Risultati Vincitore Grêmio(4º titolo) Secondo Corinthians Statistiche Miglior marcatore Washington(Ponte Preta), 11 gol Incontri disputati 117 Gol segnati 371 (3,17 per incontro) Cronologia della competizione 2000 2002 Manuale La Coppa del Brasile 2001 (ufficialmente in por…

Coppa del Brasile 2004Copa do Brasil 2004 Competizione Coppa del Brasile Sport Calcio Edizione 16ª Organizzatore CBF Date dal 4 febbraio 2004al 30 giugno 2004 Luogo Brasile Partecipanti 64 Risultati Vincitore Santo André(1º titolo) Secondo Flamengo Statistiche Miglior marcatore Alex Alves (Botafogo) e Dauri (15 de Novembro),8 gol Incontri disputati 114 Gol segnati 325 (2,85 per incontro) Pubblico 698 012 (6 123 per incontro) Cronologia della compe…
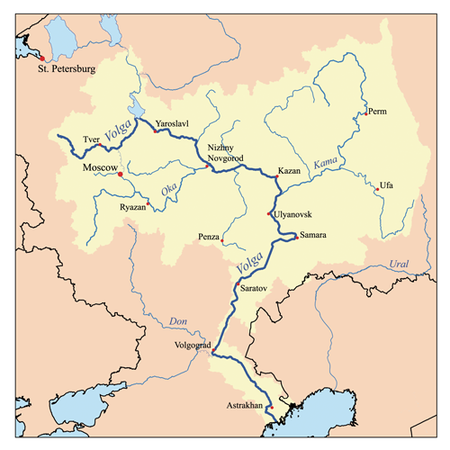
River in Russia; longest river in Europe For other uses, see Volga (disambiguation). Wolga redirects here. For the genus of rotifers, see Wolga (rotifer). VolgaThe Volga at YaroslavlMap of the Volga drainage basinEtymologyProto-Slavic *vòlga wetnessNative nameВолга (Russian)LocationLocationEastern EuropeCountryRussian FederationCitiesTver, Yaroslavl, Nizhny Novgorod, Cheboksary, Kazan, Ulyanovsk, Samara, Saratov, Volgograd, Astrakhan, TogliattiPhysical characteristicsSource …

Italian composer Tarquinio MerulaBackground informationBorn(1595-11-24)24 November 1595Busseto, ItalyDied10 December 1665(1665-12-10) (aged 70)Cremona, ItalyGenresBaroqueOccupation(s)Composer, organist, violinistInstrument(s)OrganviolinYears active1616–1665Musical artist Tarquinio Merula (24 November 1595 – 10 December 1665) was an Italian composer, organist, and violinist of the early Baroque era. Although mainly active in Cremona, stylistically he was a member of the Venetian school. …

Australian Paralympic swimmer Ashleigh McConnellPersonal informationFull nameAshleigh McConnellNationalityAustralianBorn (1996-03-26) 26 March 1996 (age 28)Melbourne, VictoriaSportSportSwimmingClassificationsS9, SB8, SM9ClubMelbourne VicentreCoachKenrick Monk Medal record Women's paralympic swimming Representing Australia Paralympics 2016 Rio de Janeiro 4x100 m freestyle 34 pts 2020 Tokyo 4×100 m freestyle 34 pts IPC Swimming World Championships 2015 Glasgow 4x100 m freestyle Co…

E T Reed - Prehistoric Peeps Book Prehistoric Peeps was a cartoon series written and drawn by Edward Tennyson Reed starting in the 1890s. The cartoon appeared in Punch magazine. A collection of the cartoons was published under the title Mr. Punch's Prehistoric Peeps in 1894.[1] The cartoon series was adapted into a series of live-action silent films, including Prehistoric Peeps (1905).[2] References ^ Bissette, Steve (12 May 2008). The First Dinosaur Comic: Prehistoric Peeps! (te…

Earl Marischal ScotlandArms of the house of Keith, hereditary holders of the title of Earl Marischal.George Keith, Earl Marischal ke-10, pemegang terakhir jabatan Earl MarischalJenisPejabat Tinggi NegaraDibentukc. 1160 (Dibentuk Marischal dari Skotlandia)c. 1458 (Diangkat menjadi Bangsawan sebagai Earl Marischal)Pejabat pertamaHervey de Keithsebagai Marischal dari SkotlandiaWilliam Keith, Earl Marischal ke-1sebagai Earl MarischalPejabat terakhirGeorge Keith, Earl Marischal ke-10Sukse…

Pakistani psychiatrist and Islamic scholar (1956–2010) Muhammad Farooq KhanBorn1956 (1956)Swabi Mardan Division, Khyber-Pakhtunkhwa, PakistanDied2 October 2010 (aged 53–54)Baghdada, Mardan, PakistanEraModern eraRegionKhyber Pakhtunkhwa, PakistanSchoolFarahi-IslahiMain interestsIslamic law and Quranic exegesisNotable ideasSeparation of fiqh (Islamic jurisprudence) from Sharia (Divine law) Websitewww.drfarooqkhan.com Muhammad Farooq Khan was a Pakistani psychiatrist, scholar of I…

Railway station in Mersin, Turkey MERSİNMersin Railway Station from the south east.General informationOwned byTCDDPlatforms4Tracks7HistoryOpened1886Rebuilt1955ElectrifiedNoServices Preceding station TCDD Taşımacılık Following station Terminus Mersin–İskenderun Tırmıltowards İskenderun Mersin–İslahiye Tırmıltowards İslahiye Mersin–Adana Tırmıltowards Adana LocationMERSİNLocation within Turkey Mersin station (Turkish: Mersin istasyonu) is the main railway terminal in the city…

Artist's conception of an O-type star Main-sequence star of spectral type O Hertzsprung–Russell diagram Spectral type O B A F G K M L T Brown dwarfs White dwarfs Red dwarfs Subdwarfs Main sequence(dwarfs) Subgiants Giants Red giants Blue giants Bright giants Supergiants Red supergiant Hypergiants absolutemagni-tude(MV) An O-type main-sequence star (O V) is a main-sequence (core hydrogen-burning) star of spectral type O and luminosity class V. These stars have between 15 and 90 times the mass o…

American attorney This article is about the attorney and civil servant. For the legislator, see Mary Jo White (Pennsylvania politician). Mary Jo White31st Chair of the U.S. Securities and Exchange CommissionIn officeApril 10, 2013 – January 20, 2017PresidentBarack ObamaPreceded byElisse B. WalterSucceeded byMichael Piwowar (Acting)United States Attorney for the Southern District of New YorkIn officeJune 1993 – January 7, 2002PresidentBill ClintonGeorge W. BushPreceded byOtt…

The Magic HourJapanese posterSutradaraKōki MitaniDitulis olehKōki MitaniDistributorTohoTanggal rilis 07 Juni 2008 (2008-06-07) NegaraJapanPendapatankotor$36,023,586[1] The Magic Hour (ザ・マジックアワーcode: ja is deprecated ) adalah film Jepang produksi tahun 2008 bergenre komedi yang ditulis dan disutradarai oleh Kōki Mitani. Film yang dirilis pada 7 Juni 2008, ini dibintangi oleh Kōichi Satō sebagai Taiki Murata, Satoshi Tsumabuki sebagai Noboru Bingo, Toshiyuki Nis…

Himno NacionalB. Indonesia: Lagu Kebangsaan UruguayLagu kebangsaan UruguayPenulis lirikFrancisco Acuña de Figueroa, 1833KomponisFrancisco José Debali, 1845Penggunaan1948Sampel audioHimno Nacional (Vocal)berkasbantuan Sampel audioLagu kebangsaan Uruguayberkasbantuan Himno Nacional merupakan lagu kebangsaan di Uruguay. Lagu ini pertama kali dinyanyikan pada tahun 1833. Penulis lagu ini adalah Francisco Acuña de Figueroa. Lirik Orientales, la Patria o la Tumba! Libertad o con gloria m…

Perú 20.mo puesto Titular Alternativo Datos generales Asociación FPF Confederación Conmebol Seudónimo La BlanquirrojaLa Bicolor Ranking FIFA 11.er lugar (junio de 2018) Participación 5.ª Mejor resultado Cuartos de final (1970) Entrenador Ricardo Gareca Estadísticas Partidos 3 Goles anotados 2 (0.67 por partido) Goles recibidos 2 (0.67 por partido) Goleadores André CarrilloPaolo Guerrero(Un gol) Cronología Anterior España 1982 Siguiente Por definir La selección del Perú fue uno de los…

يوهان ويلاند معلومات شخصية الميلاد 24 يناير 1981 (العمر 43 سنة)بوروس الطول 1.88 م (6 قدم 2 بوصة)[1][1] مركز اللعب حارس مرمى الجنسية السويد مسيرة الشباب سنوات فريق 0000–1997 Rydboholms SK 1997–2000 إلفسبورغ المسيرة الاحترافية1 سنوات فريق م. (هـ.) 2000–2008 إلفسبورغ 206 (0) 2009–2015 كوبنهاغن…



