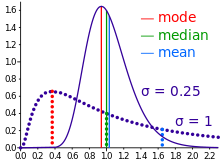
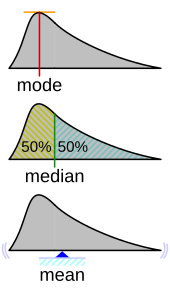
Mean
|
Read other articles:

Горная пехота Украиныукр. Гірська піхота України Годы существования 1996 — н. в. Страна Украина Входит в Сухопутные войска Тип горная пехота Функция Боевые действия в горах Знаки отличия Горная пехота Украины (укр. Гірська піхота України) — род войск в составе Сухопут…

العلاقات الأنغولية القيرغيزستانية أنغولا قيرغيزستان أنغولا قيرغيزستان تعديل مصدري - تعديل العلاقات الأنغولية القيرغيزستانية هي العلاقات الثنائية التي تجمع بين أنغولا وقيرغيزستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية �…

Further information: Evansville, Indiana Evansville, Indiana is the home to two minor league professional sports teams and one amateur sports team. The city is also the home to two NCAA collegiate teams, and nine high schools that participate in the Indiana High School Athletic Association. Evansville is also the host to the annual Hoosier Nationals and Demolition City Roller Derby. Professional teams Club League Sport Venue Established Championships Evansville Otters Frontier League Baseball Bo…

Origin LtdJenisUmum (ASX: ORG)IndustriEnergiDidirikan2000 tetapi sebagian bisnis dimulai pada abad ke-19Kantorpusat Sydney, New South Wales, AustraliaTokohkunciGrant King, MDProdukMinyak, gas dan listrikPendapatan $6.94 miliar AUD (2009, [1])Laba bersih $530 juta dipotong pajak AUD (2009)Karyawan~4000Situs webwww.originenergy.com.au Origin adalah sebuah perusahaan energi Australia yang berpusat di Sydney. Sektor bisnis Origin Energy aktif dalam sejumlah sektor dalam bisnis energi: Eksploras…

Chronologies Groupe d'enfants et d'adolescents, 5 janvier 1972.Données clés 1969 1970 1971 1972 1973 1974 1975Décennies :1940 1950 1960 1970 1980 1990 2000Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocrat…

This template does not require a rating on Wikipedia's content assessment scale.It is of interest to multiple WikiProjects. Anthropology This template is within the scope of WikiProject Anthropology, a collaborative effort to improve the coverage of Anthropology on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.AnthropologyWikipedia:WikiProject AnthropologyTemplate:WikiProject AnthropologyAnthropology art…

Disambiguazione – Se stai cercando altri significati, vedi College (disambigua). Questa voce sull'argomento istruzione è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Corpus Christi College, uno dei collegi costituenti dell'Università di Cambridge in Inghilterra. Il termine college (dal latino collegium) è usato soprattutto nei paesi anglofoni per denotare una scuola secondaria con studenti interni o u…

Ular Koros Ular jali Ptyas korros Status konservasiHampir terancamIUCN192131 TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSquamataFamiliColubridaeGenusPtyasSpesiesPtyas korros Schlegel, 1837 lbs Ular Koros (Ptyas korros) adalah spesies ular tikus yang tersebar luas di Asia Tenggara. Nama umumnya dalam bahasa Inggris adalah Chinese ratsnake atau Indo-chinese ratsnake. Morfologi Panjang tubuh ular koros mencapai 2.5 meter. Tubuh bagian atas berwarna abu-abu, perak, atau kecokelatan, seda…

Untuk kegunaan lain, lihat Arab. Sebuah persiapan festival kebudayaan Arab di Moroko. Budaya Arab merupakan kawasan berbudaya Arab meliputi wilayah Jazirah Arabia, Mesir dan Afrika Utara demikian pula dengan Irak yang dahulunya dalam pengaruh budaya Persia dan Syria yang berkebudayaan Byzantium. pada saat ini meliputi wilayah Timur Tengah, Bulan Sabit Subur, Teluk Persia, dan Afrika Utara.[1] Budaya ini memengaruhi budaya-budaya di bagian Asia lainnya—terutama di Asia Selatan, Asia Ten…

1919 treaty Treaty of Neuilly-sur-SeineBulgaria after the Treaty of Neuilly-sur-SeineSigned27 November 1919LocationNeuilly-sur-Seine, FranceConditionRatification by Bulgaria and four Principal Allied Powers.Signatories Bulgaria United States British Empire France Italy Japan Other Allied Powers Greece Kingdom of Serbs, Croats and Slovenes Belgium China Cuba Hejaz Poland Portugal Romania Siam Czechoslovakia …

Unicameral legislature of the Indian state of Gujarat Gujarat Legislative Assembly15th Gujarat AssemblyState Emblem of GujaratTypeTypeUnicameral of the Gujarat Legislative Assembly Term limits5 yearsHistoryPreceded by15th Gujarat Legislative AssemblyLeadershipSpeakerShankar Chaudhary, BJP since 20 December 2022[3] Deputy SpeakerJethabhai Ahir, BJP since 20 December 2022[4] Leader of the House (Chief Minister)Bhupendrabhai Patel, BJPsince 13 September 2021 Leader of t…

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторичн�…

Ini adalah nama Korea; marganya adalah Dong. TaeyangTaeyang pada Juni 2016LahirDong Young-bae18 Mei 1988 (umur 35)Uijeongbu, Gyeonggi-do, Korea SelatanNama lainSolPekerjaan Penyanyi penulis lagu Suami/istriMin Hyo-rin (m. 2018)Anak1Karier musikGenre Hip hop Pop Korea Dansa R&B Dansa elektronik Instrumen Vokal Piano Gitar Drum Tahun aktif2006–sekarangLabel YG (2006-2022) YGEX (2006-2022) THE BLACK LABEL (2022-sekarang) Artis terkait Big Bang Teddy Pa…

Town and former municipality in Northwestern Region, IcelandBlönduósbærTown and former municipalityHouses in BlönduósBlönduósbærCoordinates: 65°40′N 20°18′W / 65.667°N 20.300°W / 65.667; -20.300CountryIcelandRegionNorthwestern RegionConstituencyNorthwest ConstituencyMunicipalityHúnabyggðEstablished1876Area • Total183 km2 (71 sq mi)Population • Total895 • Density4.73/km2 (12.3/sq mi)Postal code(s)540…

American labor leader Herb SorrellSorrell in 1946BornHerbert Knott Sorrell(1897-04-18)April 18, 1897Deepwater, Missouri[1]DiedMay 7, 1973(1973-05-07) (aged 76)[2]Burbank, California, United StatesNationalityAmericanOccupation(s)Trade union organizer and activist Herbert Knott Sorrell (April 18, 1897 – May 7, 1973) was an American labor leader and Hollywood union organizer.[3] He headed the Conference of Studio Unions (CSU) in the late 1940s, and was the business ma…

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロー…

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府與�…

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для плануван�…

NGC 4143 الكوكبة السلوقيان[1] رمز الفهرس NGC 4143 (الفهرس العام الجديد)UGC 7142 (فهرس أوبسالا العام)PGC 38654 (فهرس المجرات الرئيسية)2MASX J12093608+4232031 (Two Micron All-Sky Survey, Extended source catalogue)MCG+07-25-036 (فهرس المجرات الموروفولوجي)Z 215-39 (فهرس المجرات وعناقيد المجرات)UZC J120936.1+423203 (فهرس زفيكي المحدّث)Z 1207…

Ивен, или Рыцарь со львомфр. Yvain ou le Chevalier au Lion Жанр Chivalric novel[вд] Автор Кретьен де Труа Язык оригинала старофранцузский язык Дата первой публикации 1170 Предыдущее Рыцарь телеги, или Ланселот Следующее Персеваль, или Повесть о Граале Медиафайлы на Викискладе «Иве́н, или Р…







![{\displaystyle (4\times 36\times 45\times 50\times 75)^{\frac {1}{5}}={\sqrt[{5}]{24\;300\;000}}=30.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b516046ef2a7b8b23301b7ab228cec73f38e062)