Inégalité FKG
|
Read other articles:

Samarra terletak 125 km di sebelah utara Bagdad Sāmarrā (سامراء) adalah sebuah kota kecil yang terletak di sisi timur Sungai Tigris di Provinsi Salah ad Din, Irak. Terletak pada koordinat 34°11′N 43°52′E / 34.183°N 43.867°E / 34.183; 43.867, kota ini berlokasi 125 km di sebelah utara Bagdad. Penduduknya berjumlah 201.700 jiwa (2002). Pada masa lampau, Samarra merupakan salah satu kota terbesar Mesopotamia. Meskipun kota ini termasuk tempat suci bagi kaum S…

High-rise office building in the Nine-Twelve District of downtown Cleveland, Ohio The CentennialThe former Huntington Bank BuildingFormer namesUnion Commerce Bank BuildingGeneral informationTypeOffice/Hotel/Retail/Residential (Mixed Use)Location925 Euclid Avenue Cleveland, Ohio 44115 United StatesConstruction started1921Completed1924Cost12.234 MillionHeightRoof88.09 m (289 ft)Technical detailsFloor count21Floor areaover 1,000,000 sq. ft.Design and constructionArchitect(s)Graham, Anders…

Christy CanyonCanyon, Februari 2006Lahir17 Juni 1966 (umur 57)[1]Pasadena, California, Amerika SerikatNama lainChristie Canyon, Cristy Canyon, Missy, Tara White, Sara Wine, Tara Wine, Linda Daniel, DeeDeeTinggi5 ft 7 in (1,70 m)Berat130 pon (59 kg; 9,3 st)Situs webwww.christycanyon.com Christy Canyon (lahir 17 Juni 1966)[1] adalah mantan aktris porno dan penyiar radio asal Amerika Serikat.[3] Dirinya telah dilantik menjadi anggota H…

Bubukṣah dan Gagangaking (variasi nama: Bubhuksah, Bela-belu yang dalam versi lisan Jawa modern terkadang ditambah gelar syekh, Gagakaking, Dami Aking) adalah suatu cerita rakyat didaktis yang popular dari masa Majapahit, dan hingga sekarang diwariskan turun-temurun, baik secara lisan maupun tertulis (pada helai lontar, khususnya di Bali). Kisah ini diabadikan di beberapa candi dan potongan relief di Jawa Timur yang merupakan peninggalan Majapahit, seperti Candi Penataran, Candi Gambar Wetan, …

Candi Wringin Branjang Candi Wringin Branjang adalah sebuah candi terletak di Desa Gadungan, Kecamatan Gandusari, Kabupaten Blitar, Jawa Timur. Candi ini letaknya masih satu kompleks dengan Situs Gadungan, jaraknya sekitar 100 m di sebelah barat Situs Gadungan I. Arsitektur Candi Wringin Branjang terdiri dari beberapa teras, dan teras ketiga adalah letak Candi Wringin Branjang. Di teras-teras selanjutnya terdapat beberapa bangunan, dan terdapat altar tanpa bilik di teras tertinggi. Terdapat bebe…

Google MapsTangkapan layar Google Maps di sebuah peramban webURLGoogle MapsTipePemetaan webPerdagangan ?YaRegistration (en)Opsional, terikat dengan akun GoogleLangueMultilingualBahasa pemrogramanC++ (back-end), JavaScript, XML, Ajax (UI)PemilikGooglePembuatGoogle Web DeveloperGoogle Service entry (en)8 Februari 2005; 19 tahun lalu (2005-02-08)Lokasi kantor pusatMountain View KeadaanAktifBlog resmihttps://blog.google/products/maps/ Google Maps (Indonesia: Peta Googlecode: id is deprecat…

University law school in Ohio, US This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (June 2015) (Learn how and when to remove this template message) University of Akron School of LawMottoFiat LuxEstablished1921School typePublicParent endowment$133.3 million[1]DeanEm…

У этого термина существуют и другие значения, см. Прохождение. Прохождение Луны по диску Земли, снимки получены 16 июля 2015 года спутником DSCOVR с расстояния 1 млн миль от Земли, видна лишь обратная сторона Луны Прохожде́ние, или астрономи́ческий транзи́т — астрономическ�…
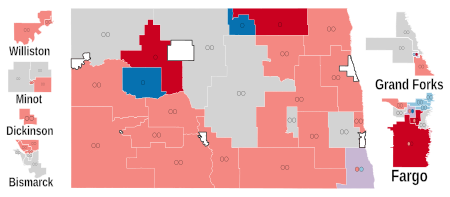
Legislative election in North Dakota Not to be confused with 2022 United States House of Representatives election in North Dakota.This article needs to be updated. Please help update this article to reflect recent events or newly available information. (February 2023)2022 North Dakota House of Representatives election ← 2020 November 8, 2022 2024 → 66 of the 94 seats in the North Dakota House of Representatives48 seats needed for a majority Majority party Minority pa…

For the band of the same name, see Reckless Kelly (band). 1993 Australian filmReckless KellyTheatrical release posterDirected byYahoo SeriousWritten byYahoo SeriousWarwick RossDavid RoachLulu SeriousProduced byYahoo SeriousWarwick RossStarringYahoo SeriousMelora HardinAlexei SayleHugo WeavingCinematographyKevin HaywardEdited byLawrence JordanMusic byAnthony MarinelliTommy Tycho[1]ProductioncompanySerious ProductionsDistributed byRoadshow Entertainment[2]Release date 8 April&…

Not to be confused with ECAC Hockey, a separate NCAA Division I conference. Sports federation of colleges and universities in the eastern United States Eastern College Athletic ConferenceAssociationNCAAFounded1938CommissionerDan Coonan (since 2017)Sports fielded 15 men's: 13 women's: 13 DivisionI, II, IIINo. of teams220HeadquartersDanbury, Connecticut, U.S.RegionEast CoastOfficial websitehttp://www.ecacsports.comLocations The Eastern College Athletic Conference (ECAC) is a college athletic confe…

27th running of the Indianapolis 500 27th Indianapolis 500Indianapolis Motor SpeedwayIndianapolis 500Sanctioning bodyAAADateMay 30, 1939WinnerWilbur ShawWinning EntrantBoyle Racing HeadquartersAverage speed115.035 mph (185.131 km/h)Pole positionJimmy SnyderPole speed130.138 mph (209.437 km/h)Most laps ledLouis Meyer (79)Pre-racePace carBuick Roadmaster 80Pace car driverCharles ChayneStarterSeth Klein[1]Honorary refereePaul G. Hoffman[1]Estimated attendance145,…

Kolkata Municipal Corporation in West Bengal, IndiaWard No. 5Kolkata Municipal CorporationInteractive Map Outlining Ward No. 5Ward No. 5Location in KolkataCoordinates: 22°36′32″N 88°22′47″E / 22.608889°N 88.379694°E / 22.608889; 88.379694Country IndiaStateWest BengalCityKolkataNeighbourhoods coveredTala, BelgachiaReservationOpenParliamentary constituencyKolkata UttarAssembly constituencyKashipur-BelgachhiaBurough1Population (2011) • Total…

Caserne des Tourelles Caserne des Tourelles en 2014, siège de la DGSE. Construction 1878 - 1881 Coordonnées 48° 52′ 28″ nord, 2° 24′ 25″ est Géolocalisation sur la carte : France Géolocalisation sur la carte : Paris modifier La caserne des Tourelles est une ancienne caserne militaire située 133-161 boulevard Mortier dans le 20e arrondissement de Paris, qui fut un camp d'internement pendant la Seconde Guerre mondiale, puis le siège, ap…

Voce principale: Campionato mondiale di Formula 1 2000. Gran Premio della Malesia 2000 663º GP del Mondiale di Formula 1Gara 17 di 17 del Campionato 2000 Data 22 ottobre 2000 Luogo Circuito di Sepang Percorso 5,543 km Circuito permanente Distanza 56 giri, 310,408 km Clima Sereno Risultati Pole position Giro più veloce Michael Schumacher Mika Häkkinen Ferrari in 1'37397 McLaren - Mercedes in 1'38453 (nel giro 34) Podio 1. Michael SchumacherFerrari 2. David CoulthardMcLaren - Mercedes 3. …

This article is about the Soyuz-M rocket. For other Soyuz variants, see Soyuz (rocket family). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Soyuz-M – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Soyuz-MFunctionCarrier rocketManufacturerOKB-1Country o…

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды…

Dettaglio della statua in marmo del San Giovanni Battista Ecce Agnus Dei Girolamo Santacroce (Nola, 1502 – Napoli, 1537) è stato uno scultore, architetto e medaglista italiano. Indice 1 Biografia 2 Opere 3 Bibliografia 4 Altri progetti 5 Collegamenti esterni Biografia Altare del Santacroce nella chiesa di Sant'Agnello Maggiore (parzialmente smembrato) Cenni biografici riguardo l'infanzia del Santacroce sono testimoniati dall'opera di Bernardo De Dominici: Vite de' pittori, scultori, ed archit…

مدرسة عمادية مدرسه عمادیه مدرسة عمادية معلومات الموقع الجغرافي المدينة جرجان البلد إيران تعديل مصدري - تعديل مدرسة عمادية هي مدرسة تاريخية تعود إلى السلالة الصفوية، وتقع في جرجان.[1] مراجع ^ Encyclopaedia of the Iranian Architectural History. Cultural Heritage, Handicrafts and Tourism Organization of Iran. 19 مايو 2011.…

Season of television series Season of television series How I Met Your MotherSeason 1Season 1 DVD cover artStarring Josh Radnor Jason Segel Cobie Smulders Neil Patrick Harris Alyson Hannigan No. of episodes22ReleaseOriginal networkCBSOriginal releaseSeptember 19, 2005 (2005-09-19) –May 15, 2006 (2006-05-15)Season chronologyNext →Season 2 List of episodes The first season of How I Met Your Mother, an American sitcom created by Carter Bays and Craig Thomas, premiered on CBS…



![{\displaystyle \mathbb {E} \left[XY\right]\geq \mathbb {E} \left[X\right]\mathbb {E} \left[Y\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/796dc0c97b1a2ec4d328429e4ebd6ac2b6dfbc28)












![{\displaystyle \mathbb {E} \left[f(Z)g(Z)\right]\geq \mathbb {E} \left[f(Z)\right]\mathbb {E} \left[g(Z)\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d3bf368cbe4a8883b404861f2bc7e2a8090ea4)




![{\displaystyle {\begin{aligned}0&\leq \int _{{\mathcal {O}}\times {\mathcal {O}}}\ (X(\omega )-X(\omega ^{\prime })(Y(\omega )-Y(\omega ^{\prime })\ \mathbb {Q} \otimes \mathbb {Q} (d\omega ,d\omega ^{\prime })\\&=\int _{{\mathcal {O}}\times {\mathcal {O}}}\ [X(\omega )Y(\omega )+X(\omega ^{\prime })Y(\omega ^{\prime })-X(\omega )Y(\omega ^{\prime })-X(\omega ^{\prime })Y(\omega )]\ \mathbb {Q} \otimes \mathbb {Q} (d\omega ,d\omega ^{\prime })\\&=2\ \mathbb {E} \left[XY\right]-2\ \mathbb {E} \left[X\right]\mathbb {E} \left[Y\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/589ed179a59bd869583a8cab89b6ace2dd15f2e9)



![{\displaystyle {\begin{aligned}0&\leq \mathbb {E} \left[\left(f(Z)-f(Z^{\prime }\right)\,\left(g(Z)-g(Z^{\prime }\right)\right]\\&=\mathbb {E} \left[f(Z)g(Z)\right]+\mathbb {E} \left[f(Z^{\prime })g(Z^{\prime })\right]-\ \mathbb {E} \left[f(Z^{\prime })g(Z)\right]-\mathbb {E} \left[f(Z)g(Z^{\prime })\right]\\&=2\ \mathbb {E} \left[f(Z)g(Z)\right]-\ \mathbb {E} \left[f(Z^{\prime })\right]\mathbb {E} \left[g(Z)\right]-\mathbb {E} \left[f(Z)\right]\mathbb {E} \left[g(Z^{\prime })\right]\\&=2\ \mathbb {E} \left[f(Z)g(Z)\right]-\ 2\mathbb {E} \left[f(Z)\right]\mathbb {E} \left[g(Z)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d6ecd598838b04a4225704f72408c94cdf13892)

![{\displaystyle \scriptstyle \ [\![1,n]\!].\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/571ccf78a14ecc06d0090d0205adaa762dc639c8)





![{\displaystyle \scriptstyle \ J=[\![1,n]\!],\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a54c901663a8a1336feaad3580c5490ca1ec3f95)
![{\displaystyle {\begin{aligned}{\widehat {X}}(\omega _{n})&=\int _{{\mathcal {O}}^{n-1}}\ X(\omega )\ \mathbb {Q} (d\omega _{1})\dots \mathbb {Q} (d\omega _{n-1})\\&=\mathbb {E} \left[X\left|\omega _{n}\right.\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5e1fff70e3e262ed8a0f9cea3dea03e05352e25)





![{\displaystyle \mathbb {E} \left[{\widehat {X}}{\widehat {Y}}\right]\geq \mathbb {E} \left[{\widehat {X}}\right]\mathbb {E} \left[{\widehat {X}}\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c5f36e5dbbe684bff48745784c2734e4496ad26)
![{\displaystyle {\begin{aligned}\mathbb {E} \left[{\widehat {X}}\right]\mathbb {E} \left[{\widehat {Y}}\right]&=\mathbb {E} \left[\mathbb {E} \left[X\left|\omega _{n}\right.\right]\right]\ \mathbb {E} \left[\mathbb {E} \left[Y\left|\omega _{n}\right.\right]\right]\\&=\mathbb {E} \left[X\right]\mathbb {E} \left[Y\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/542846bd177fb5c7464bb29050f8acc59736c67e)
![{\displaystyle \scriptstyle \ {\tilde {\Omega }}={\mathcal {O}}^{[\![1,n-1]\!]},\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/598a111dcd9cb6a62f8bca59d7729c1ec0fb0dcc)

![{\displaystyle {\begin{aligned}{\tilde {\mathbb {E} }}\left[Z\right]&=\int _{{\mathcal {O}}^{n-1}}\ Z(\omega )\ \mathbb {Q} (d\omega _{1})\dots \mathbb {Q} (d\omega _{n-1}).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d404a6c8cd7496cf4caeac369a06633863ff586e)



![{\displaystyle {\tilde {\mathbb {E} }}\left[{\tilde {X}}\right]={\widehat {X}}(\omega _{n})=\mathbb {E} \left[X\left|\omega _{n}\right.\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7655d467a66437082ba7bc51a73055b0c283fad)
![{\displaystyle {\tilde {\mathbb {E} }}\left[{\tilde {Y}}\right]={\widehat {Y}}(\omega _{n})=\mathbb {E} \left[Y\left|\omega _{n}\right.\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b47ee445b130052f3135007824f1f7b73ff5461)
![{\displaystyle \mathbb {E} \left[XY\left|\omega _{n}\right.\right]={\tilde {\mathbb {E} }}\left[{\tilde {X}}{\tilde {Y}}\right]\geq {\tilde {\mathbb {E} }}\left[{\tilde {X}}\right]{\tilde {\mathbb {E} }}\left[{\tilde {Y}}\right]={\widehat {X}}(\omega _{n}){\widehat {Y}}(\omega _{n}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19a4a0d8325f86e4b012757b771468722bfce3cb)
![{\displaystyle \mathbb {E} \left[XY\right]=\mathbb {E} \left[\mathbb {E} \left[XY\left|\omega _{n}\right.\right]\right]\geq \mathbb {E} \left[{\widehat {X}}{\widehat {Y}}\right]\geq \mathbb {E} \left[X\right]\mathbb {E} \left[Y\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d91375ce5957e104af03f99d6fe06034b65594cf)