Matrice tridiagonale
|
Read other articles:

The following is a list of highest grossing Philippine films. Color key – is an entry film for Metro Manila Film Festival. Nine hundred million mark Year Title Production company Box office Source 2023 Rewind Star Cinema, APT Entertainment, AgostoDos Pictures ₱902 million [1] Eight hundred million mark Year Title Production company Box office Source 2019 Hello, Love, Goodbye Star Cinema ₱880 million [2][3] 2018 The Hows of Us Star Cinema ₱810 million [4…

Bagian dari Kodeks Leningrad menampilkan Keluaran 15:21-16:3. Walaupun Kitab Perjanjian Lama merupakan hasil sebuah proses kanon, kritik kanon berfokus pada bentuk akhir dari teks. Kritik kanonik atau disebut juga Kritik kanon adalah salah satu metode atau pendekatan yang dipakai dalam menafsir Alkitab berdasarkan teks Alkitab yang sudah jadi dalam tradisi Kristen.[1][2][3] Kritik Kanon selalu merujuk pencetusnya, yaitu Brevard S. Child.[2][4] Pendekatan a…

Genre of traditional music of Mexico RancheraStylistic originsMariachiCultural originsMexicoDerivative formscorridoOther topicschilenahuapangoJarabe TapatíoMexican zapateadomariachiNorteñoRegional Mexicanson mexicanoTejano Ranchera (pronounced [ranˈtʃeɾa]) or canción ranchera is a genre of traditional music of Mexico. It dates to before the years of the Mexican Revolution. Rancheras today are played in the vast majority of regional Mexican music styles. Drawing on rural traditional…
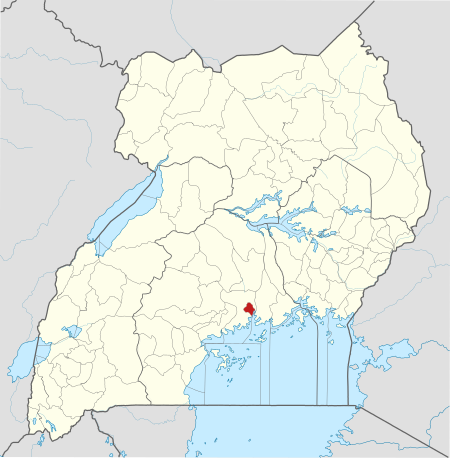
Hospital in Central Region, UgandaKawempe Specialised National Referral HospitalUganda Ministry of Health andKampala Capital City AuthorityGeographyLocationKawempe, Kampala, Central Region, UgandaCoordinates00°21′43″N 32°33′41″E / 0.36194°N 32.56139°E / 0.36194; 32.56139OrganisationCare systemPublicTypeGeneralServicesEmergency departmentIIIBeds200HistoryOpened2016 [1]LinksOther linksHospitals in UgandaMedical education in Uganda Kawempe General Hospita…

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Kabupaten Kepulauan Meranti – berita · surat kabar · buku · cendekiawan · JSTOR Kabupaten Kepulauan MerantiKabupatenTranskripsi bahasa daerah • Abjad Jawiكڤولاوان مرنتيFestival Cian…

Commercial offices in Atlanta, GeorgiaCoastal States BuildingCoastal States Building (2006)General informationStatusCompletedTypeCommercial officesAddress260 Peachtree Street NEAtlanta, Georgia 30303Coordinates33°45′37″N 84°23′13″W / 33.760257°N 84.387072°W / 33.760257; -84.387072Construction started1970Completed1971HeightRoof115 m (377 ft)Technical detailsFloor count27Design and constructionArchitect(s)Sidney R. Barrett & AssociatesReferences …

Constituency of Bangladesh's Jatiya Sangsad Gaibandha-5Constituencyfor the Jatiya SangsadDistrictGaibandha DistrictDivisionRangpur DivisionElectorate313,755 (2018)[1]Current constituencyCreated1984PartyAwami LeagueMember(s)Mahmud Hasan Ripon← Seat no. 32Seat no. 33Seat no.34 → Gaibandha-5 is a constituency represented in the Jatiya Sangsad (National Parliament) of Bangladesh since 2023 by Mahmud Hasan Ripon of the Awami League. Boundaries The constituency encompasses Fulchhari and Sa…

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Птиц�…

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) Commune in Hauts-de-France, FranceSteenwerckCommuneThe church in Steenwerck Coat of ar…

40ZrZirkoniumBatang kristal dan kubus zirkonium 1 cm3 Garis spektrum zirkoniumSifat umumNama, lambangzirkonium, ZrPengucapan/zirkonium/[1] Penampilanputih keperakanZirkonium dalam tabel periodik 40Zr Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Oksigen Fluor Neon Natrium Magnesium Aluminium Silikon Fosfor Sulfur Clor Argon Potasium Kalsium Skandium Titanium Vanadium Chromium Mangan Besi Cobalt Nikel Tembaga Seng Gallium Germanium Arsen Selen Bromin Kripton Rubidium Stronti…
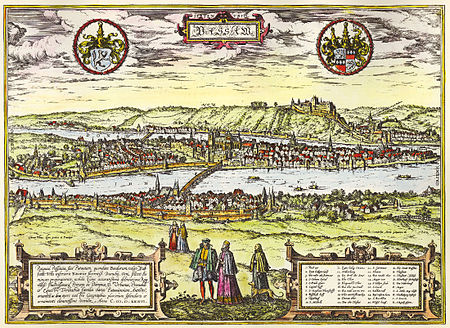
University town in Lower Bavaria, Germany This article is about the town. For the district, see Passau (district). Batavis redirects here. For the plural, see Batavi (disambiguation). Town in Bavaria, GermanyPassau TownDonaulände and Old town FlagCoat of armsLocation of Passau Passau Show map of GermanyPassau Show map of BavariaCoordinates: 48°34′28″N 13°27′53″E / 48.57444°N 13.46472°E / 48.57444; 13.46472CountryGermanyStateBavariaAdmin. regionNiederbayern Di…

Italian-Scottish classical violinist For the Italian modern pentathlete, see Nicola Benedetti (pentathlete). Nicola BenedettiCBEBenedetti at the EXPO festivals event at The Hub, Edinburgh, 2023Background informationBorn (1987-07-20) 20 July 1987 (age 36)Irvine, North Ayrshire, ScotlandGenresClassicalOccupation(s)ViolinistYears active2005–presentLabelsDeutsche GrammophonUniversal Classics and JazzDecca RecordsWebsitewww.nicolabenedetti.co.ukMusical artist Nicola Joy Nadia Benedetti CBE (bo…

Pour les articles homonymes, voir Graziani. Rodolfo GrazianiFonctionsMinistre de la Défense République Sociale italienne 23 septembre 1943 - 25 avril 1945. Gouverneur Général de la Libye italienne Royaume d'Italie 1er juillet 1940 - 25 mars 1941.BiographieNaissance 11 août 1882Filettino (royaume d'Italie)Décès 11 janvier 1955 (à 72 ans)RomeSépulture AffileNom de naissance Rodolfo GrazianiNationalité italienneAllégeances Royaume d'Italie, République sociale italienneFormation Aca…
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)[2…

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: IF Urædd – news · newspapers · books · scholar · JSTOR (October 2022) (Learn how and when to remove this message) Norwegian sports club IF Urædd is a Norwegian sports club from Porsgrunn, founded in 1880. Since 8 December 1993 it has been an alliance sports team, with independent…

Paulo ArnsOFMKardinal, Uskup Agung Emeritus São PauloPaulo Evaristo Arns pada 1982TakhtaSão Paulo (Emeritus)Penunjukan22 Oktober 1970Awal masa jabatan1 November 1970Masa jabatan berakhir9 April 1998PendahuluAgnelo RossiPenerusCláudio HummesJabatan lainKardinal-Imam Sant’Antonio da Padova in Via TuscolanaImamatTahbisan imam30 November 1945oleh José Pereira AlvesTahbisan uskup3 Juli 1966oleh Agnelo RossiPelantikan kardinal5 Maret 1973oleh Paus Paulus VIPeringkatKardinal-ImamInforma…

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府與�…

Nightclub violence in Venezuela in 2018 This article needs to be updated. Please help update this article to reflect recent events or newly available information. (June 2019) El Paraíso stampedeThe location of El Paraíso in CaracasDate16 June 2018LocationLos Cotorros Club, Caracas, VenezuelaTypeStampedeCauseTear gas canisterDeaths19[1]Non-fatal injuries9+ The El Paraíso stampede was a stampede of more than 500 people that occurred in the early-morning hours of 16 June 2018 at the El P…

Ancient town in the Maghreb Numidia Mutugenna or Muttegena was a colonia (town) of the Roman, Berber and Vandal empires, located in the Maghreb. The city is generally identified with the ruins at Ain-Tebla in modern Algeria. Mutugenna was also the locus of a bishopric and was an important site in the development of the Donatist schism. The Diocese of Mutugenna (Dioecesis Mutugennensis) is today a suppressed and titular see of the Roman Catholic Church in the episcopal province of Numidia.[1&…

Overtime work schedule in Mainland China, 9AM-9PM, 6 days per week This article is missing information about background on other (especially non-tech) overwork cultures in China; legitimized special work hour system in Shenzhen. Please expand the article to include this information. Further details may exist on the talk page. (July 2021) 996 working hour systemChinese996工作制TranscriptionsStandard MandarinHanyu Pinyinjiǔjiǔliù gōngzuò zhì The 996 working hour system (Chinese: 996�…









![{\displaystyle \det A=a_{n,n}\det \,[A]_{\{1,\ldots ,n-1\}}-a_{n,n-1}a_{n-1,n}\det \,[A]_{\{1,\ldots ,n-2\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/762f2457717fb506dbc2f028bb84848d5c91144a)







